문제 출처: https://programmers.co.kr/learn/courses/30/lessons/42891

나의 접근 방식
#include <vector>
using namespace std;
int solution(vector<int> food_times, long long k) {
int answer = 0; // 몇 번 음식부터 다시 먹기 시작해야 하는지 출력
int size = food_times.size();
long long time = 0;
int i = 0;
while (true) {
if (food_times[i] == 0) { // 값이 0인 음식은 이미 다 먹은 거니까
i = (i + 1) % size; // 다음 인덱스로 넘어가기
continue;
}
food_times[i] -= 1; // 음식을 1초간 먹는다.
time++; // 시간을 갱신한다.
if (time == k) { // 네트워크 장애가 생기면
i = (i + 1) % size; // 그 다음 인덱스로 이동해서
int cnt = 0;
while (food_times[i] == 0) { // 0인 원소를 발견할 때마다 카운트 증가
cnt++;
if (cnt == size) {
answer = -1;
return answer;
}
// 0이 아닌 원소를 찾을 때까지 인덱스 갱신
i = (i + 1) % size;
}
// 0이 아닌 원소의 음식 번호 출력
answer = i + 1;
return answer;
}
i = (i + 1) % size; // 인덱스 갱신
}
}위 방식으로 풀었더니 효율성 테스트에서 전부 시간 초과가 발생했다. 그래서 아래처럼 모든 음식을 다 먹어서 -1을 출력하는 경우는 따로 처리해주었는데, 역시나 효율성 테스트에서 0점을 받았다.
#include <vector>
using namespace std;
int solution(vector<int> food_times, long long k) {
int answer = 0; // 몇 번 음식부터 다시 먹기 시작해야 하는지 출력
int size = food_times.size();
long long clearTime = 0; // 전체 음식 다 먹는 데 걸리는 시간
for (int i = 0; i < size; i++) {
clearTime += food_times[i];
}
// 음식을 다 먹고나서 네트워크 장애가 발생한 경우, -1 출력
if (k >= clearTime) {
answer = -1;
return answer;
}
long long time = 0;
int i = 0;
while (true) {
if (food_times[i] == 0) { // 값이 0인 음식은 이미 다 먹은 거니까
i = (i + 1) % size; // 다음 인덱스로 넘어가기
continue;
}
food_times[i] -= 1; // 음식을 1초간 먹는다.
time++; // 시간을 갱신한다.
if (time == k) { // 네트워크 장애가 발생하면
i = (i + 1) % size;
// 0이 아닌 원소를 찾을 때까지 인덱스 갱신
// 모두 0인 경우는 이미 처리한 상태
while (food_times[i] == 0) {
i = (i + 1) % size;
}
// 0이 아닌 원소의 음식 번호 출력
answer = i + 1;
return answer;
}
i = (i + 1) % size; // 인덱스 갱신
}
}답안
참고한 사이트 (이미지 출처는 유튜브 강의)
https://ansohxxn.github.io/programmers/132/
https://www.youtube.com/watch?v=Knmo90E42ls
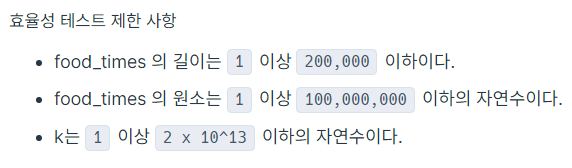
위의 제한 사항을 다시 보면, k는 무려 20조까지 커질 수 있다. 그런데 내가 위에서 풀었던 방법으로 food_times 배열을 k번 만큼 ‘순환적으로’ 순회하면서 1씩 감소시켜서 답을 구하면 (즉, O(k)이면) 효율성 테스트는 절대 통과할 수 없다. 따라서 k번 순회하지 않고 답을 도출할 수 있는 효율적인 방법을 생각해야 한다!!
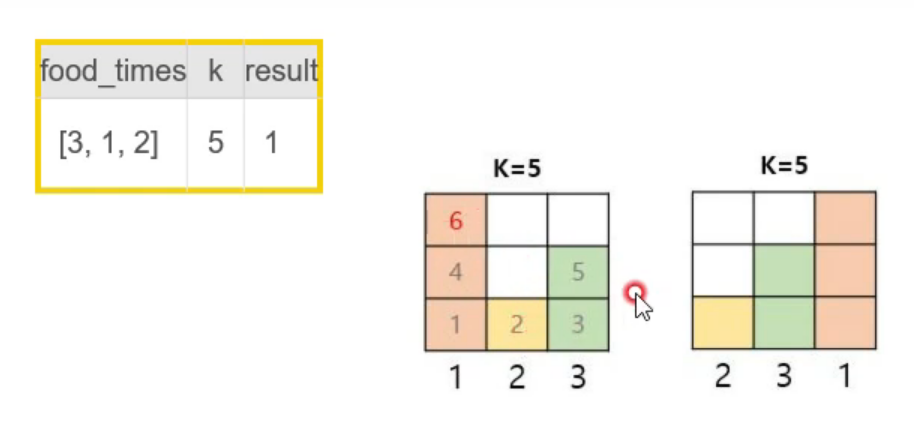
왼쪽 그림은 1, 2, 3번 음식을 차례대로 순회하면서 5초가 지난 뒤에 몇 번째 음식을 먹을지 결정하는 경우이다. 이렇게 하면 시간복잡도가 O(k)여서 더 효율적인 방법이 필요하다. 오른쪽 그림에서 그 아이디어를 얻을 수 있다. 우선 음식을 먹는 데 걸리는 시간이 적은 순으로 오름차순 정렬을 한다. 그리고 나서 제일 아래줄부터 한꺼번에 처리를 해준다. 다시 말해서, 5에서 3을 빼고 2를 뺀 뒤에 남아 있는 '1번' 음식이 5초가 지난 뒤에 먹게 될 음식인 것이다! 이 방법대로 하면 연산을 2번만 해도 답을 구할 수 있다!

입력의 크기를 늘려서 생각해보자. 왼쪽 그림처럼 1~6번까지 차례대로 순회하면서 각 음식을 먹는 데 걸리는 시간을 1씩 줄여나가면, 20초가 지난 뒤에는 4번 음식을 먹게 된다. 반면에 오른쪽 그림처럼 음식을 먹는 데 걸리는 시간에 따라 오름차순 정렬을 먼저 하고, 제일 아래줄부터 한꺼번에 처리를 해보자.
20 - 1*6 = 14
14 - 2*5 = 4
4 - 2*3 = ?
k = 4일 때는 2*3을 전부 빼지 말고 나머지 연산 값을 구해야 한다. N을 음식의 개수라고 했을 때 위 그림에서 K % N = 4 % 3 = 1 이라는 결과가 나오는데, 이 말은 원래 음식의 순서대로 다시 정렬한 결과인 2, 4, 5번 중에서 인덱스 1에 해당하는 '4번' 음식을 먹을 차례라는 뜻이다!!! 이제 코드로 옮겨보자!
C++ 코드
#include<vector>
#include<algorithm>
using namespace std;
// 음식 번호를 기준으로 오름차순 정렬
bool comp(pair<int, int> a, pair<int, int> b){
return a.second < b.second;
}
int solution(vector<int> food_times, long long k){
// (음식을 먹는 데 걸리는 시간, 음식 번호)를 묶어서 저장하기
vector<pair<int, int>> foods;
int n = food_times.size(); // 처리할 음식의 개수
for (int i = 0; i < n; i++){
foods.push_back(make_pair(food_times[i], i + 1));
}
// 시간을 기준으로 오름차순 정렬
sort(foods.begin(), foods.end());
int prevTime = 0;
// auto -> vector<pair<int, int>>::iterator
// 처리해야 할 음식의 개수 n은 하나씩 줄어든다.
for (auto it = foods.begin(); it != foods.end(); it++, n--){
int gap = it->first - prevTime; // 시간 간격
long long spendTime = (long long)gap * n; // int * int -> int 범위 넘을 수도 있기 때문에 ll 타입으로 캐스팅
if(gap == 0) continue;
if(spendTime <= k){
k -= spendTime; // 여기서 k를 한번에 확 줄일 수 있다!
prevTime = it->first;
}else{
k %= n;
sort(it, foods.end(), comp); // 음식 번호를 기준으로 다시 정렬
return (it + k)->second; // k%n 인덱스에 해당하는 음식 번호 리턴
}
}
return -1; // k초 이내에 모든 음식을 다 먹은 경우
}마무리
풀이 과정을 가만히 다시 살펴보면, 오름차순 정렬을 한 뒤에 음식을 먹는 데 걸리는 시간이 짧은 것부터 먼저 처리를 하게 된다는 것을 알 수 있다. 이런 점에서 그리디 유형의 알고리즘이라고 볼 수 있다. 위에서 푼 방법 외에도 다양한 풀이가 있기 때문에 다음에 다시 시도해보자!
