그래프
그래프는 정점과 간선으로 이루어진 자료구조를 말한다.
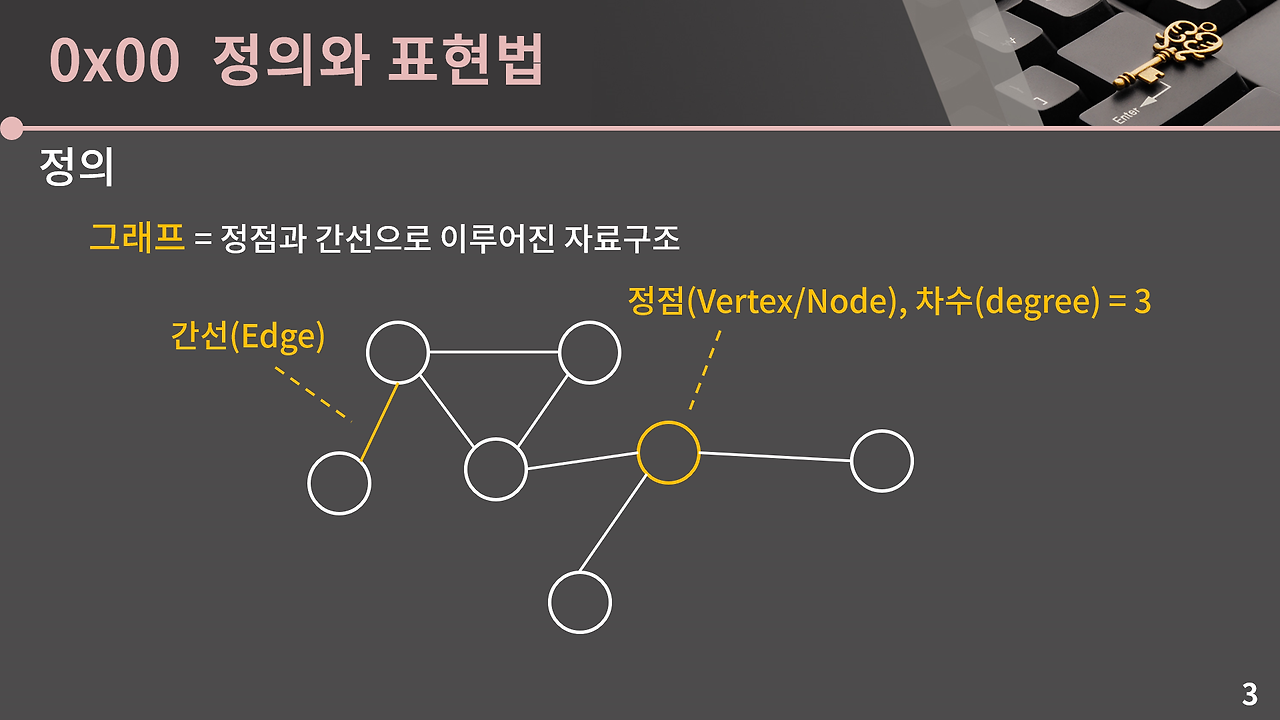
차수(degree)라는 개념을 알아두면 좋은데, 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수를 의미한다.
그래프는 네비게이션에서 최단 경로 찾기, 구글 같은 검색 엔진에서 랭킹 정하기와 같이 원소 사이의 연결 관계를 설정해야 할 때 유용하게 활용할 수 있는 자료구조이다.
그래프의 종류
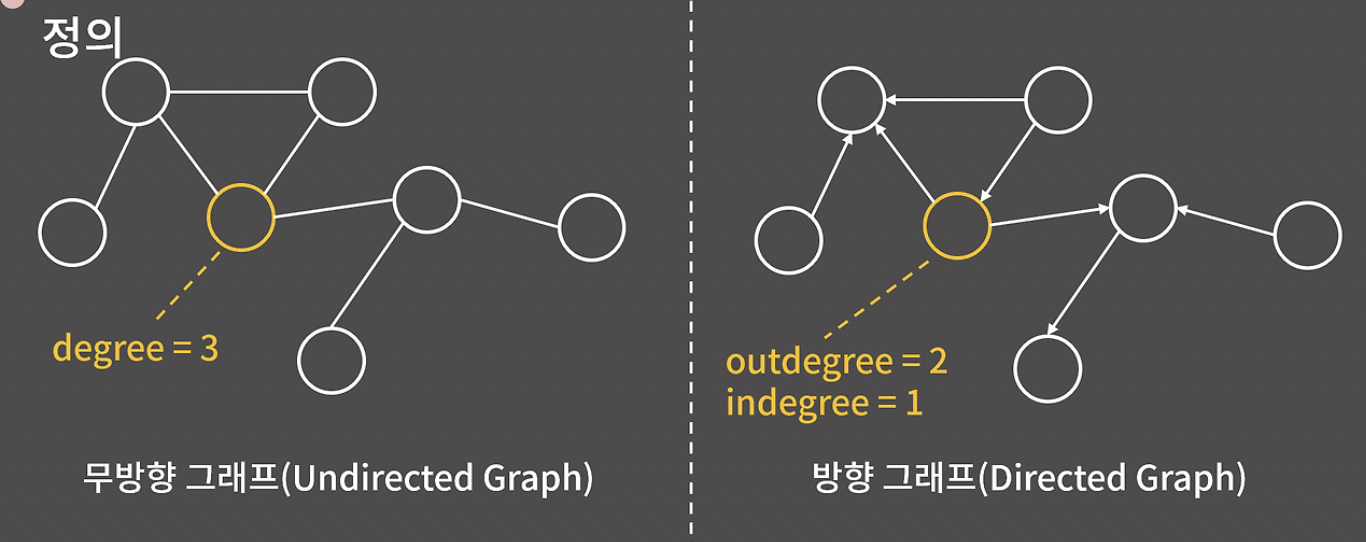
- 무방향 그래프: 간선에 방향성이 없는 그래프
- 방향 그래프: 간선에 방향성이 있는 그래프
- 진출차수(outdegree): 임의의 한 정점에서 나가는 간선의 개수
- 진입차수(indegree): 임의의 한 정점으로 들어오는 간선의 개수
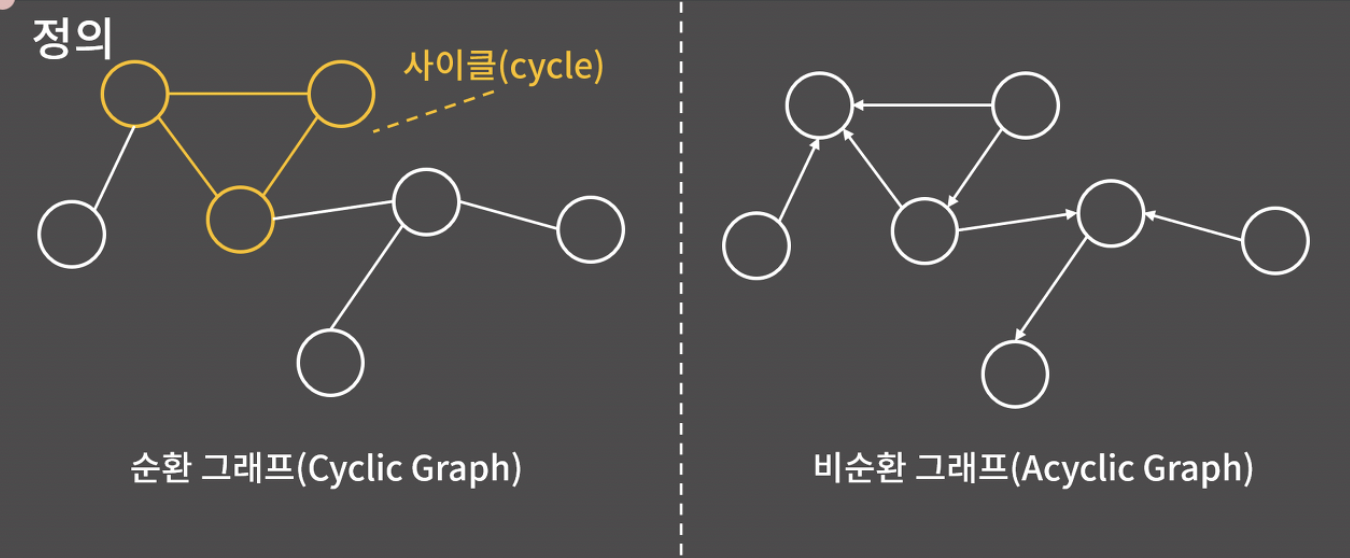
- 사이클: 임의의 한 정점에서 출발해 자기 자신으로 돌아올 수 있는 경로
- 순환 그래프: 사이클이 하나라도 있는 그래프
- 비순환 그래프: 사이클이 하나도 없는 그래프
오른쪽 그래프의 경우, 얼핏 보면 사이클이 있는 거 같지만 간선의 방향성에 의해 사이클이 아니라는 것에 유의하자.
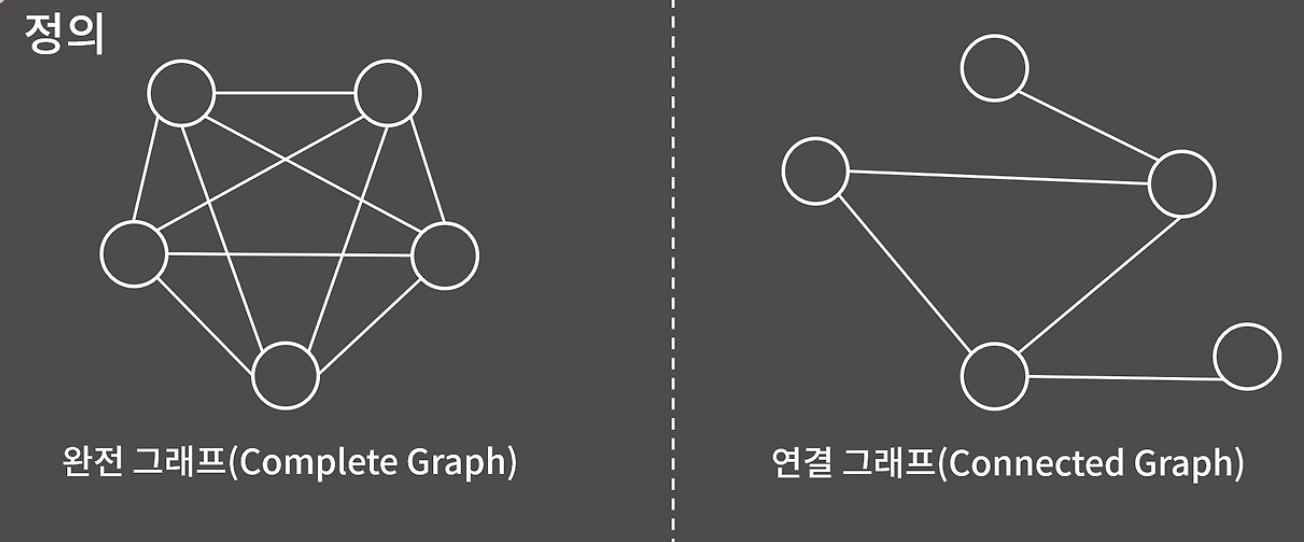
- 완전 그래프: 한 정점이 자기 자신을 제외한 모든 정점과 연결된 그래프
- 연결 그래프: 임의의 두 정점 사이에 경로가 항상 존재하는 그래프
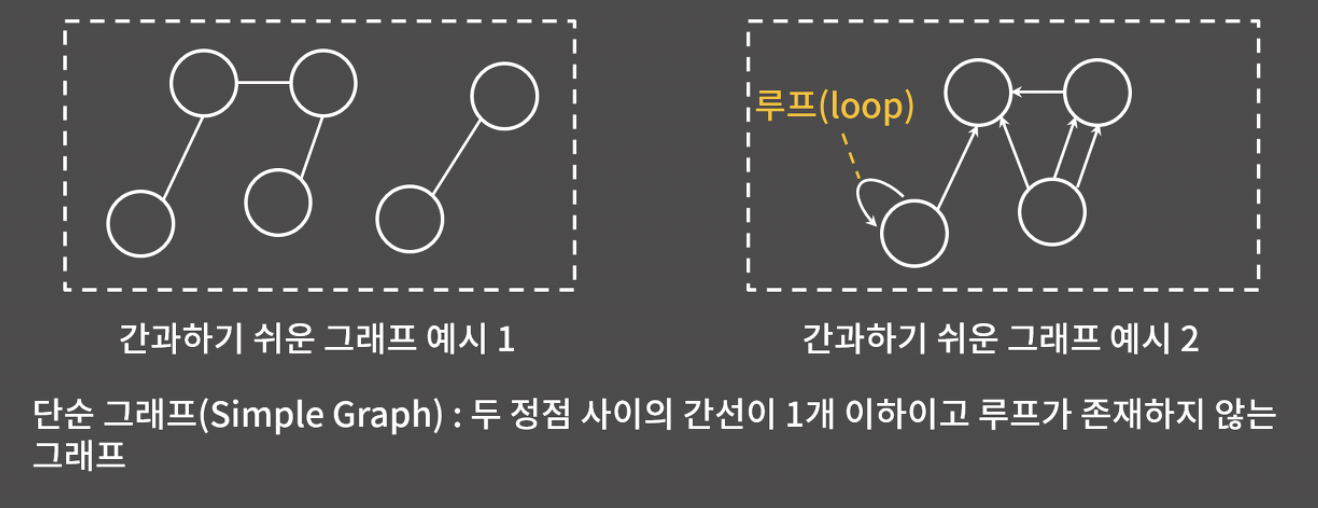
- 루프: 한 정점에서 시작해 같은 정점으로 들어오는 간선
- 단순 그래프: 두 정점 사이의 간선이 1개 이하이고, 루프가 존재하지 않는 그래프
표현 방법
인접 행렬
단순 그래프에서 두 정점이 연결되어 있으면 1, 그렇지 않으면 0을 2차원 배열에 저장한다.
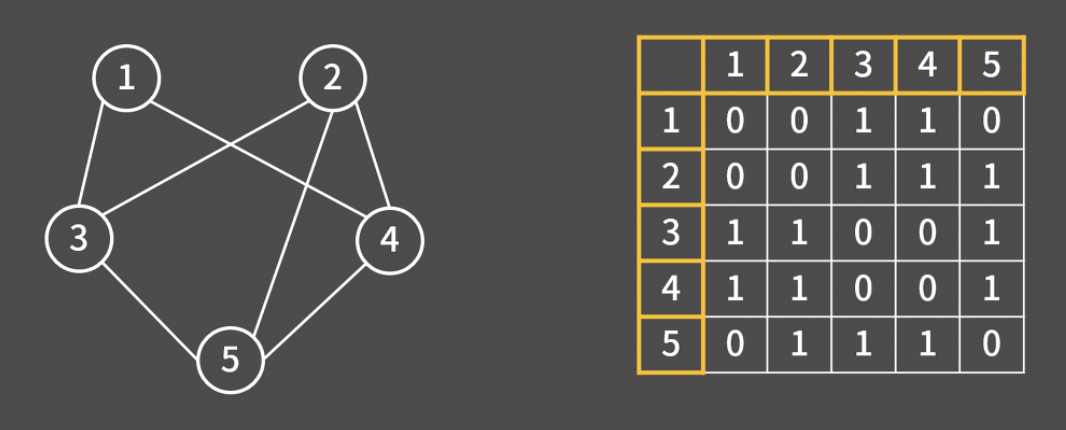
무방향 그래프를 인접 행렬로 나타내면 자연스럽게 대각선에 대해 대칭인 형태가 나온다.
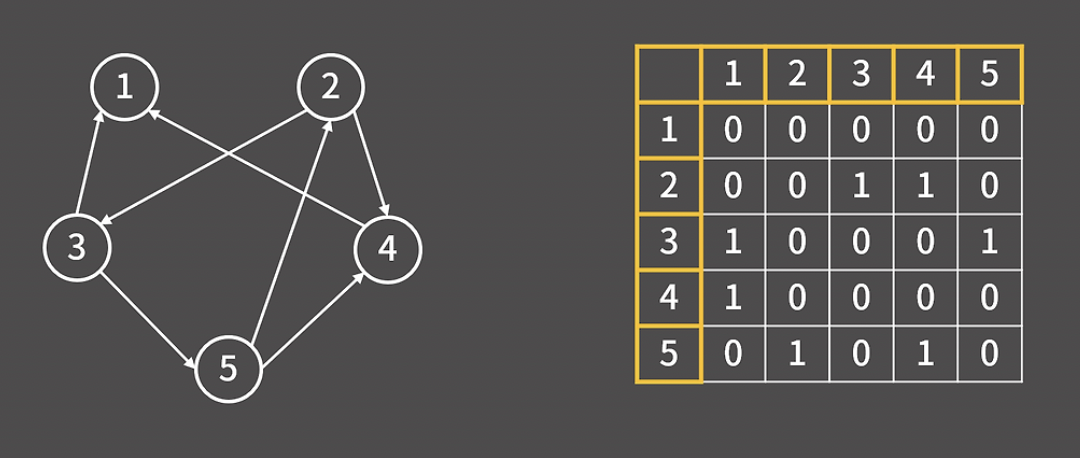
방향 그래프는 위와 같이 나타낼 수 있다.
대부분의 문제에서 주어지는 그래프는 단순 그래프인 경우가 많다. 만약 그렇지 않다면, 0이나 1만 저장하지 않고 간선의 개수를 저장하는 식으로 변형할 수 있다.
인접 리스트
인접 리스트는 인접 행렬과 비교했을 때, 정점이 많고 간선은 상대적으로 적은 경우에 공간을 절약할 수 있는 방법이다. 그리고 경우에 따라 인접 행렬로는 절대 저장이 불가능해서 인접 리스트를 써야만 하는 상황이 종종 있으므로 반드시 익숙하게 사용할 수 있어야 한다.
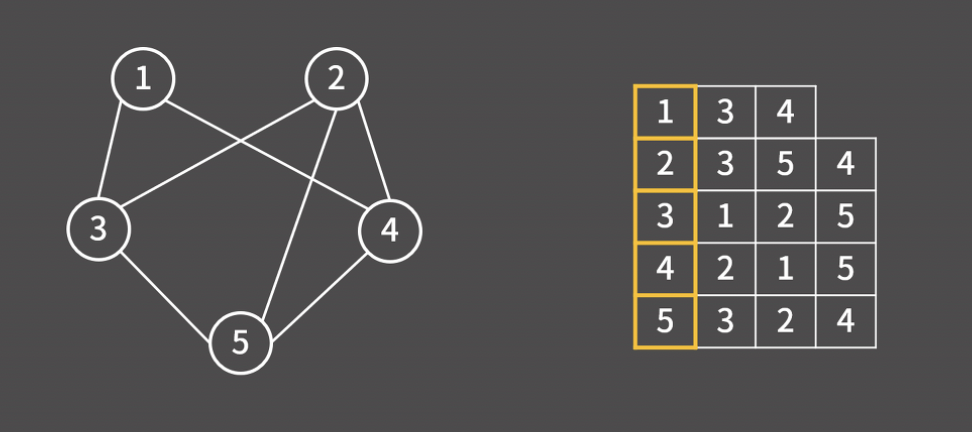
인접 리스트는 V개의 리스트를 만들고, 각 리스트에 자신과 연결된 정점들을 저장하는 방식이다.
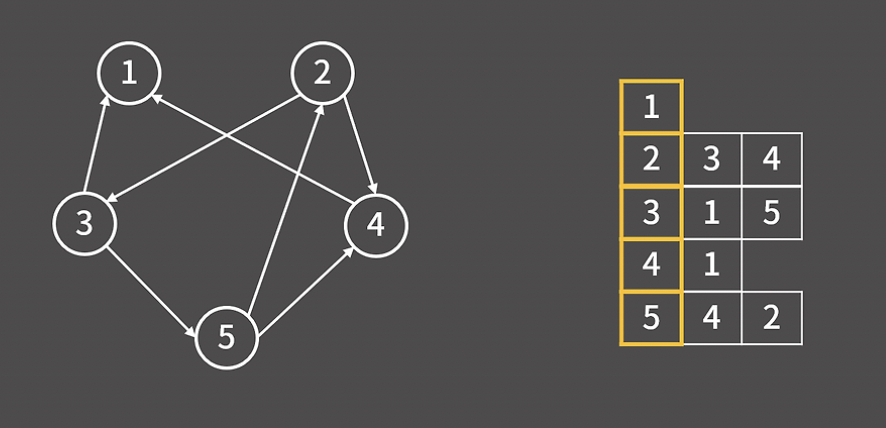
방향 그래프도 위와 같이 저장해주면 된다.
비교
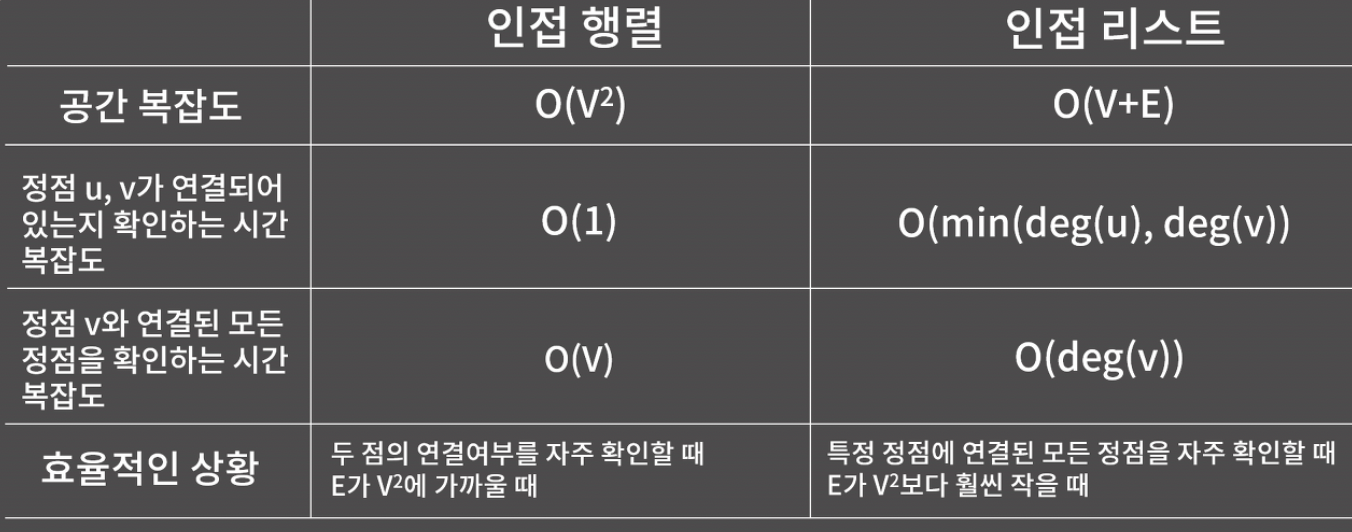
인접 리스트에서 두 정점 u, v가 연결되어 있는지 확인하려면, 한 정점에 대해 자신과 연결된 모든 정점을 확인해야 하는데 차수가 작은 것을 택하는 게 이득이므로 시간복잡도는 O(min(deg(u), deg(v)))가 된다.
한 정점에 연결된 모든 정점을 확인하는데 걸리는 시간은, 인접 행렬은 1번부터 V번까지 모두 확인해야 하므로 O(V), 인접 리스트는 본인과 연결된 정점만 확인하면 되므로 O(deg(v))가 된다.
V가 10만 이상이면 메모리 초과로 인해 인접 행렬로 나타낼 수 없는 경우가 있다. 반대로 V가 100이고 E가 7000일 때는 인접 행렬을 사용하는 게 효율적이다.
그런데 일반적인 그래프 문제에서 정점 u, v가 연결되어 있는지를 반복적으로 확인해야 하는 경우는 잘 없다. BFS, DFS, 여러 경로 알고리즘에서는 대부분 특정 정점에 연결된 모든 정점을 확인해야 하는 경우가 많다. 따라서 인접 행렬 보다는 인접 리스트로 그래프를 나타내는 상황이 훨씬 많을 것이다.
다만 입력 자체가 인접 행렬 느낌으로 주어지거나 V가 많이 작아 구현의 편의를 챙기고자 하거나, 아니면 최단경로 알고리즘 중 하나인 플로이드 알고리즘을 쓸 때에는 인접 행렬로 그래프를 나타내는 경우가 있을 수 있다.
트리
정의
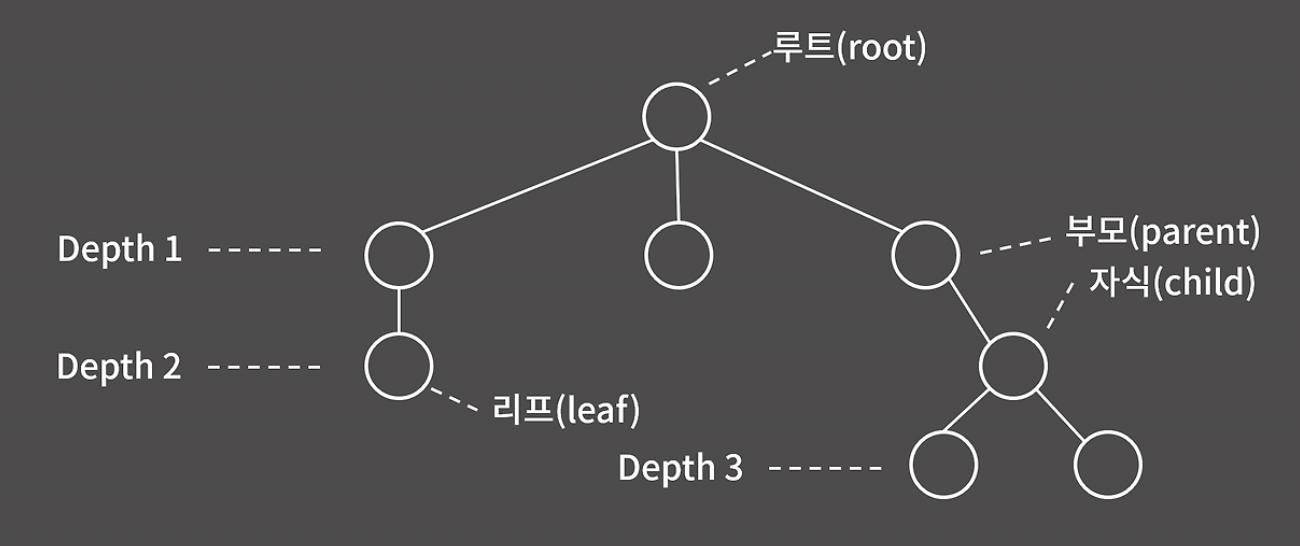
트리는 무방향이면서 사이클이 없는 연결 그래프를 의미한다.
- 무방향이면서 사이클이 없는 연결 그래프
- 연결 그래프이면서 임의의 간선을 제거하면 연결 그래프가 아니게 되는 그래프
- 임의의 두 정점을 연결하는 simple path(정점이 중복해서 나오지 않는 경로)가 유일한 그래프
- V개의 정점을 가지고, (V-1)개의 간선을 가지는 연결 그래프
- 사이클이 없는 연결 그래프이면서 임의의 간선을 추가하면 사이클이 생기는 그래프
- V개의 정점을 가지고 (V-1)개의 간선을 가지는 사이클이 없는 그래프
위의 명제들은 모두 동치이다.
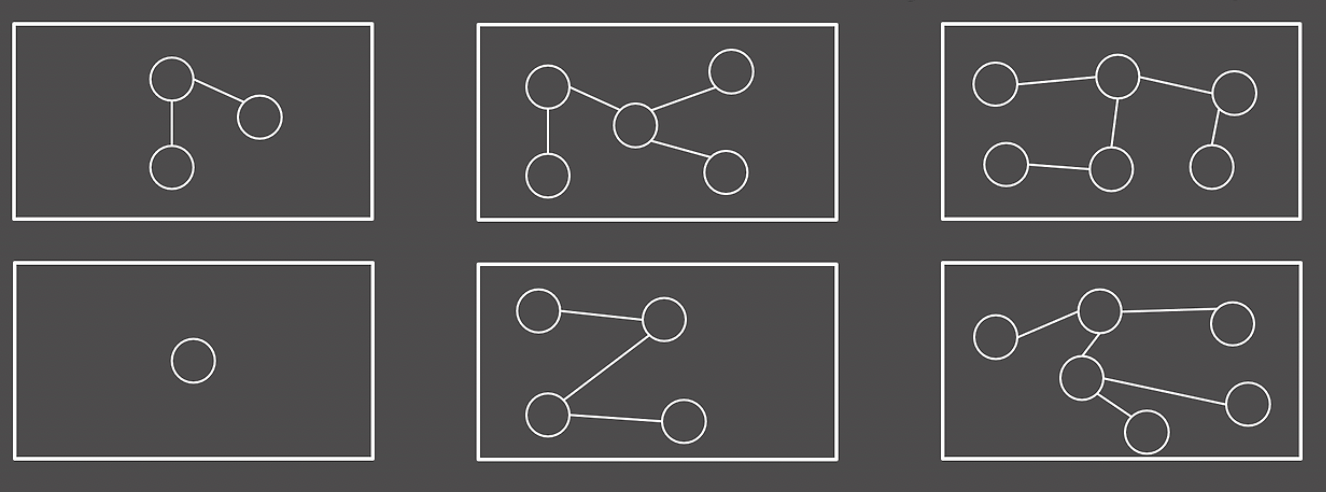
위의 그래프 모두 트리에 해당한다.
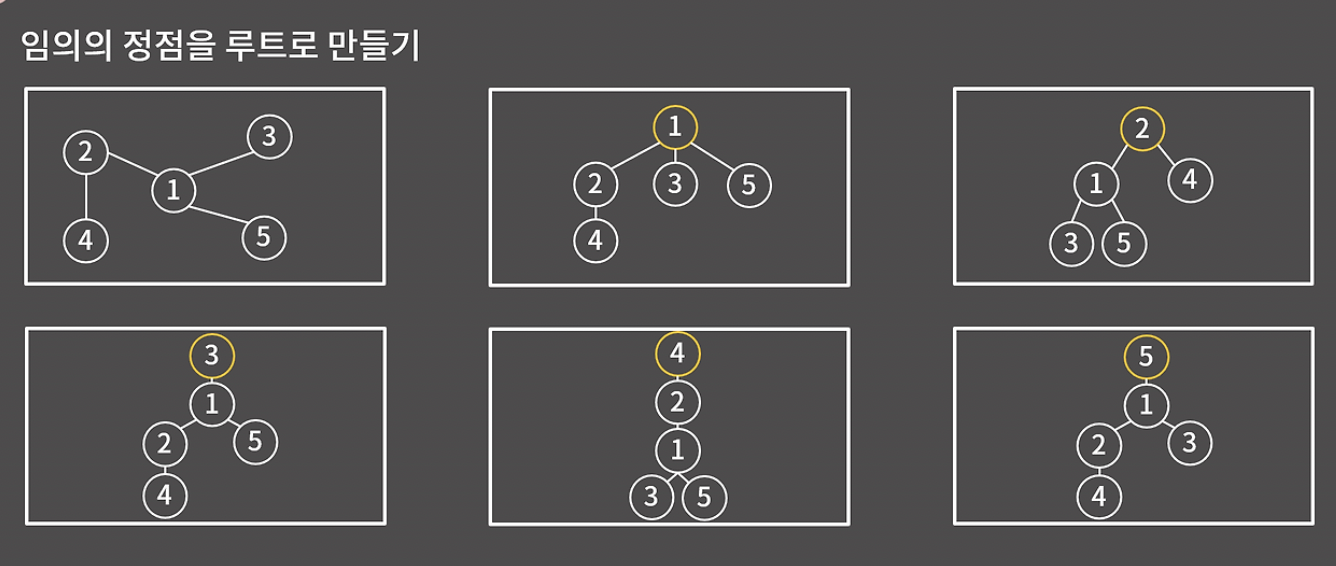
주어진 6개의 트리는 모두 같은 트리이다. 트리에서 루트가 정해지면, 나머지 모든 노드의 부모가 1개로 고정된다. 루트가 달라지면 그에 따라 각 노드의 부모 노드도 달라진다.
순회 방법
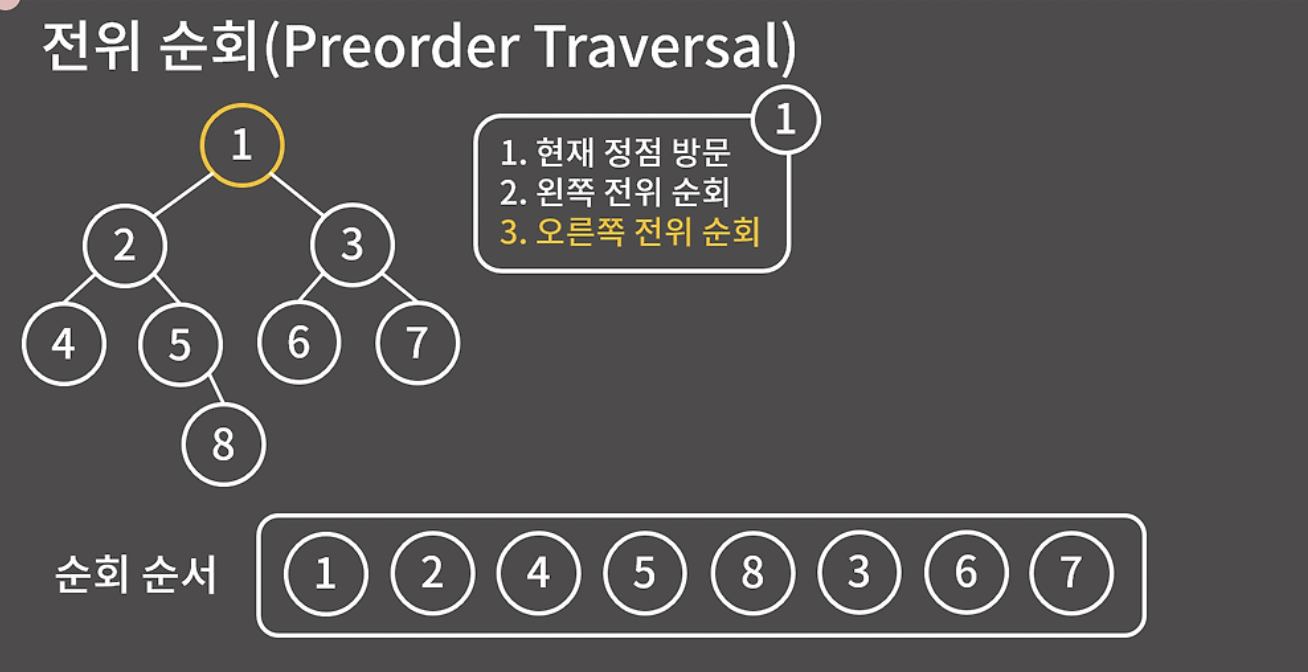
전위 순회
- 현재 정점 방문
- 왼쪽 서브 트리 전위 순회
- 오른쪽 서브 트리 전위 순회
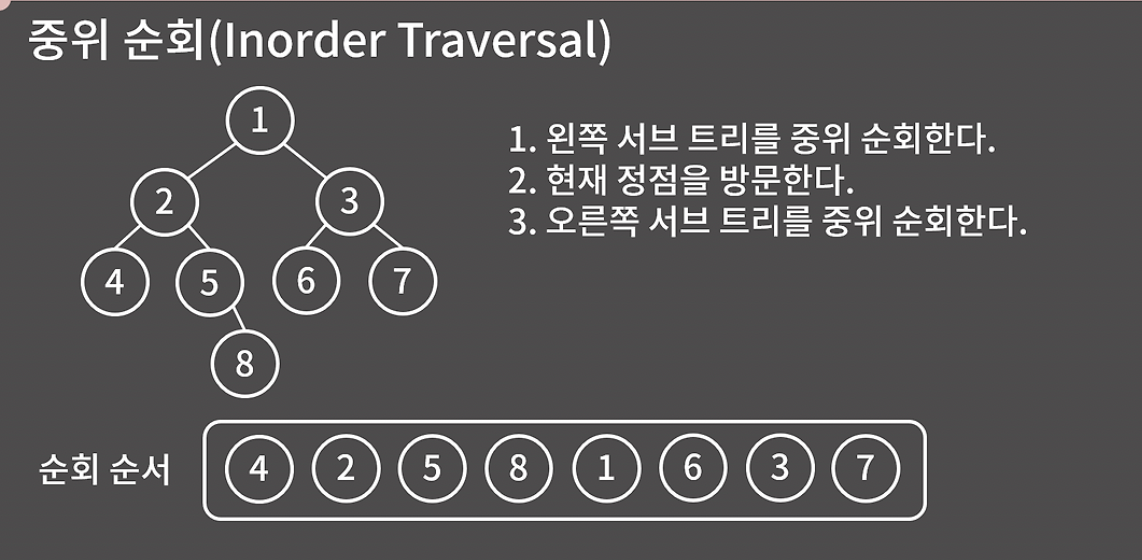
중위 순회
- 왼쪽 서브 트리 중위 순회
- 현재 정점 방문
- 오른쪽 서브 트리 중위 순회
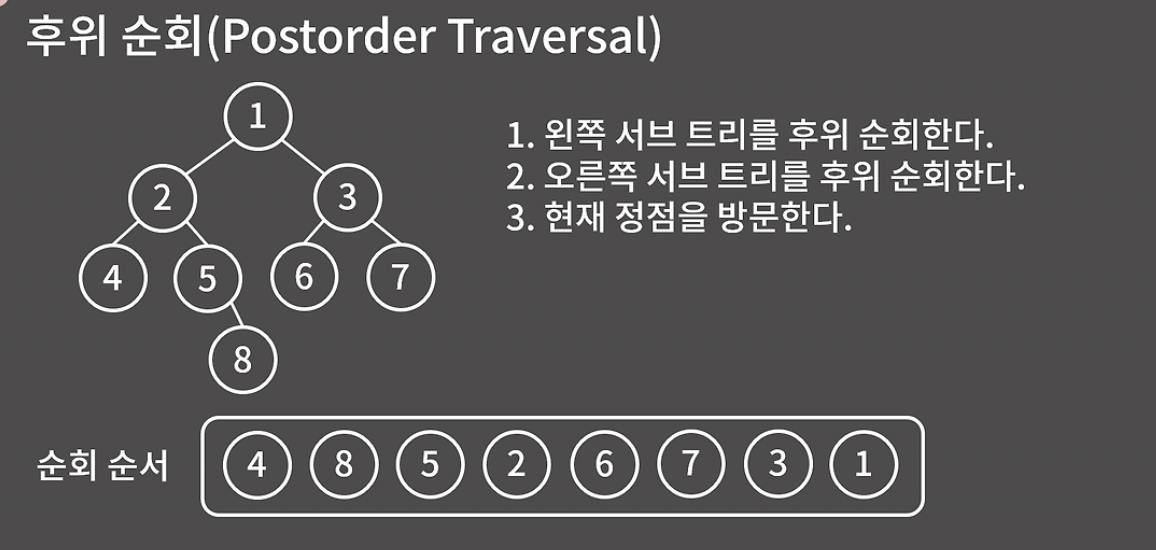
후위 순회
- 왼쪽 서브 트리 후위 순회
- 오른쪽 서브 트리 후위 순회
- 현재 정점 방문