지도학습
지도 학습의 대표적인 머신러닝 방법
[1] 분류 ( classification )
- 분류는 미리 정의된, 가능성 있는 여러 클래스 레이블(class label) 중 하나를 예측하는 것
- 두 개로만 나누는 이진 분류(Binary classification)와 셋 이상의 클래스로 분류하는 다중 분류(multiclass classification)로 나뉨
[2] 회귀 ( regression )
- 연속적인 숫자 또는 부동소수점수 (실수)를 예측하는 것
- ex) 주식 가격을 예측하여 수익을 내는 알고리즘 등
KNN의 개념과 특징
KNN 이란?
- 주변 k개의 자료의 클래스 중 가장 많은 클래스로 특정 자료를 분류하는 방식
- 새로운 자료를 가장 가까운 자료 5개의 자료(k=5)를 이용하여 투표하여 가장 많은 클래스로 할당
- Training-data 자체가 모형일 뿐 어떠한 추정 방법도 모형도 없음
- 즉, 데이터의 분포를 표현하기 위한 파라미터를 추정하지 않음- 매우 간단한 방법이지만 performance는 떨어지지 않음
- 게으른 학습(lazy learner) 또는 사례중심학습(instance-based learning)
- 게으른 학습 : 알고리즘은 훈련 데이터에서 판별 함수를 학습하는 대신 훈련 데이터 셋을 메모리에 저장하기 방법- 데이터의 차원이 증가하면 차원의 저주(curse of dimension) 문제가 발생함
- 데이터의 차원이 증가할수록 해당 공간의 크기(부피)가 기하급수적으로 증가하여 동일한 개수의 데이터의 밀도는 차원이 증가할수록 급속도로 희박해짐
- 차원의 저주 : 차원이 증가할수록 데이터의 분포 분석에 필욯나 샘플 데이터의 개수가 기하급수적으로 증가하게 되는데 이러한 어려움을 표현- i번째 관측지와 j번째 관측치의 거리로 Minkowski 거리를 이용
r = 1 : Manhattan distance
r = 2 : Euclidean distance
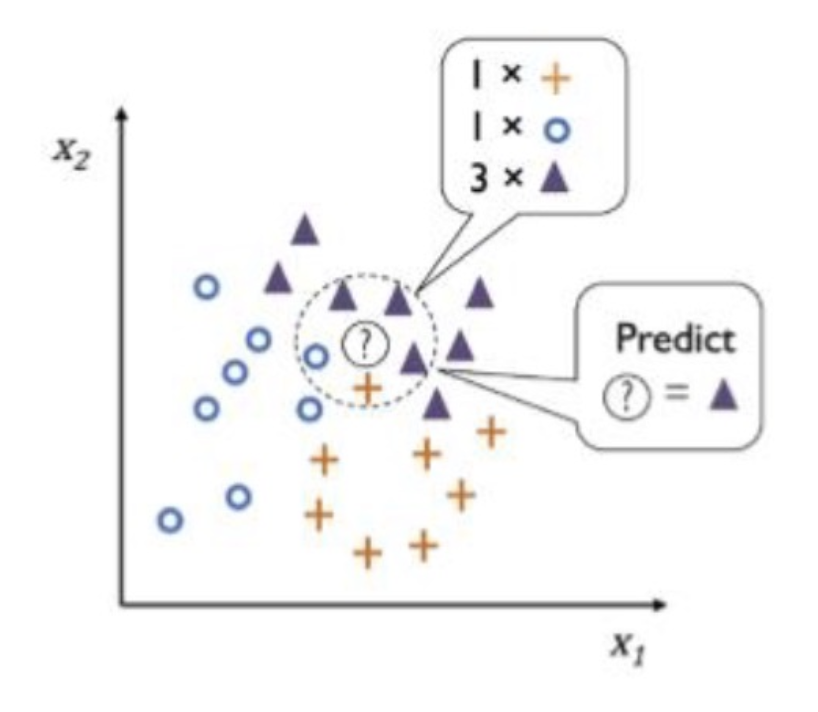
KNN의 하이퍼파라미터
탐색할 이웃 수 (k)와 거리 측정 방법
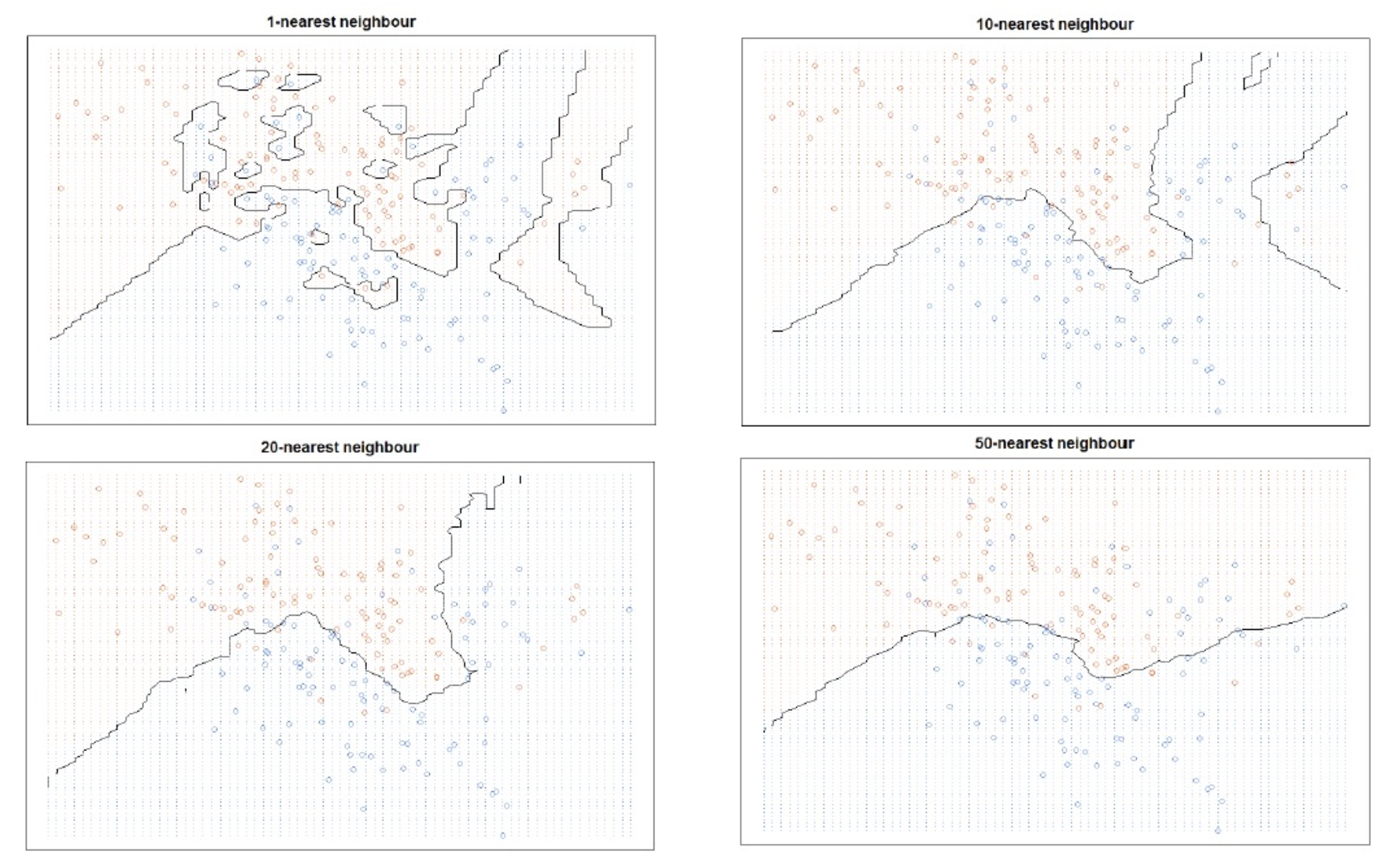
- k가 작을 경우 데이터의 지역적 특성을 지나치게 반영하여 과접합(overfitting)발생
- 반대로 매우 클 경우 모델이 과하게 정규화(underfitting) 발생
k가 가지는 의미
새로운 자료에 대해 근접치 K의 개수에 따라 Group이 달리 분류됨
- 다수결 방식(Majority voting) : 이웃 범주 가운데 빈도 기준 제일 많은 범주로 새 데이터의 범주를 예측하는 것
- 가중합 방식(Weighted voting) : 가까운 이웃의 정보에 좀 더 가중치를 부여
KNN 알고리즘의 장점과 단점
[1] 장점
- 학습데이터 내에 끼어있는 노이즈의 영향을 크게 받지 않음
- 학습데이터 수가 많다면 꽤 효과적인 알고리즘
- 마할라노비스 거리와 같이 데이터의 분산을 고려할 경우 강건한 방법론
- 마할라노비스거리(Mahalanobisdistance)는평균과의거리가표준편차의몇배인지를나타내는값
즉,어떤값이얼마나일어나기힘든값인지,또는얼마나이상한값인지를수치화하는한방법
[2] 단점
- 최적 이웃의 수(k)와 어떤 거리 척도가 분석에 적합한지 불분명해 데이터 각각의 특성에 맞게 연구자가 임의로 선정해야 함
- Best K는 데이터 마다 다르기 떄문에 탐욕적인 방식(Grid Search)으로 탐색- 새로운 관측치와 각각의 학습 데이터 사이의 거리를 전부 측정해야 하므로 계산 시간이 오래 걸리는 한계
- KNN의 계산복잡성을 줄이려는 시도들
- Locality Sensitive Hashing, Network based Indexer, Optimized product quantization
