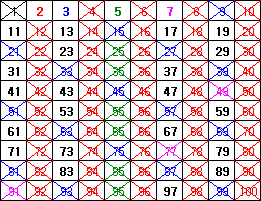
에라토스테네스의 채
소수를 판별하는 알고리즘
임의의 자연수 N에 대하여 그 이하의 소수를 가장 빠르게 찾는 방법
에라토스테네스의 체의 원리
1을 제거한다.
2를 제외한 2의 배수를 제거한다.
3을 제외한 3의 배수를 제거한다.
4는 2의 배수임으로 생략한다.
5를 제외한 5의 배수를 제거한다......
√N을 제외한 √N의 배수를 제거한다.
√N이 나오게 된 이유는 N = A*B라고 가정을 할때 A, B 모두 √N보다 클수가 없기 때문이다.
C++코드로 구현
서로 다른 2개의 수를 받은 뒤 2개의 숫자 사이의 소수를 출력하는 코드
2개의 숫자는 100000보다 작다.
(출처 백준 1929번)
#include <iostream>
#include <cmath>
using namespace std;
# define Max 1000000
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int max = 0;
int min = 0;
bool Num[Max+1] = {false}; //소수를 판별할 배열 선언
cin >> min;
cin >> max;
Num[0] = Num[1] = true; //0과 1은 소수가 아니기에 판단X
for(int i = 2; i < sqrt(Max); i++) //2부터 √Max 까지 판단
{
if(!Num[i]) //소수가 아닌 배열의 원소만 체크한다(시간 단축)
{
for(int j = i * i; j <= Max; j += i)
//i * k(k<i)까지는 모두 체크완료(ex: 13 >> 12*13까지는 판단완료)
{
Num[j] = true; //참인경우 소수
}
}
}
for(int i = min; i<= max; i++)
{
if(!K[i])
{
cout << i << "\n"; //소수인 경우 출력
}
}
}