DataStructure
✅ Array vs Linked List
메모리 저장 방식
- Array의 element들은 인접한 메모리에 위치해 저장된다. (연속적으로 할당)
- LinkedList의 element들은 메모리 어딘가 저장된다. (비연속적으로 할당)
크기
- Array의 size는 array 선언 시점에 지정되어 있다.
- Linked List의 size는 다양할 수 있다.
접근
- Array는 random access가 가능하다.
- 원소들의 index를 통해 직접적인 접근이 가능하다.
- 인덱스를 알고있다면, 시간 복잡도 : O(1)
- LinkedList는 Sequential access를 지원한다.
- element에 접근할 때, 처음부터 순차적으로 접근하면서 찾아야 한다.
- 시간 복잡도 : O(N)
삭제/삽입
- Array는 삭제/삽입시 상대적으로 시간이 더 걸린다.
- 배열의 어느 원소를 삭제한다면 배열의 연속적인 특징이 깨지게 된다. (빈 공간 생김)
- 삭제한 원소보다 큰 인덱스를 갖는 원소들을
shift 해주어야 하는 비용 발생!
- 시간 복잡도 :인덱스 접근 후 삽입 및 삭제 O(1) + 전체 배열 요소 shift O(N)
- LinkedList
- 맨 앞 혹은 맨 뒤에 삽입 및 삭제 시간 복잡도 : O(1)
- 원하는 위치에 삽입 및 삭제 시간 복잡도 : O(N)
✅ Stack and Queue
Stack
- Last In First Out (LIFO) - 나중에 들어간 원소가 먼저 나옴
Queue
- First In First Out (FIFO) - 먼저 들어간 원소가 먼저 나옴
✅ Tree
- 비선형 구조
- 계층적 관계를 표현하는 자료구조
트리를 구성하고 있는 구성요소
- Node(노드) : 트리를 구성하고 있는 각각의 요소
- Edge(간선) : 트리를 구성하기 위해 노드와 노드를 연결하는 선
- Root Node(루트 노드) : 트리 구조에서 최상위에 있는 노드
- Terminal Node(단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드
- Internal Node(내부 노드) : 단말 노드를 제외한 모든 노드, 루트 노드 포함
Level과 Height
- Level(레벨) : 각 층별로 숫자를 매긴 것, 레벨은 0부터 시작 → 루트 노드의 레벨은 0
- height(높이) : 트리의 최고 레벨
🔹 Binary Tree (이진트리)
- 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어짐
- 나뉘어진 두 서브 트리 모두 이진 트리어야 함
- Perfect Binary Tree, Complete Binary Tree, Full Binary Tree
- Perfect Binary Tree : 모든 레벨이 꽉 찬 이진 트리
- Complete Binary Tree : 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 이진트리
- Full Binary Tree : 모든 노드가 0개 혹은 2개의 자식 노드만을 갖는 이진트리
🔹 Binary Search Tree (BST)
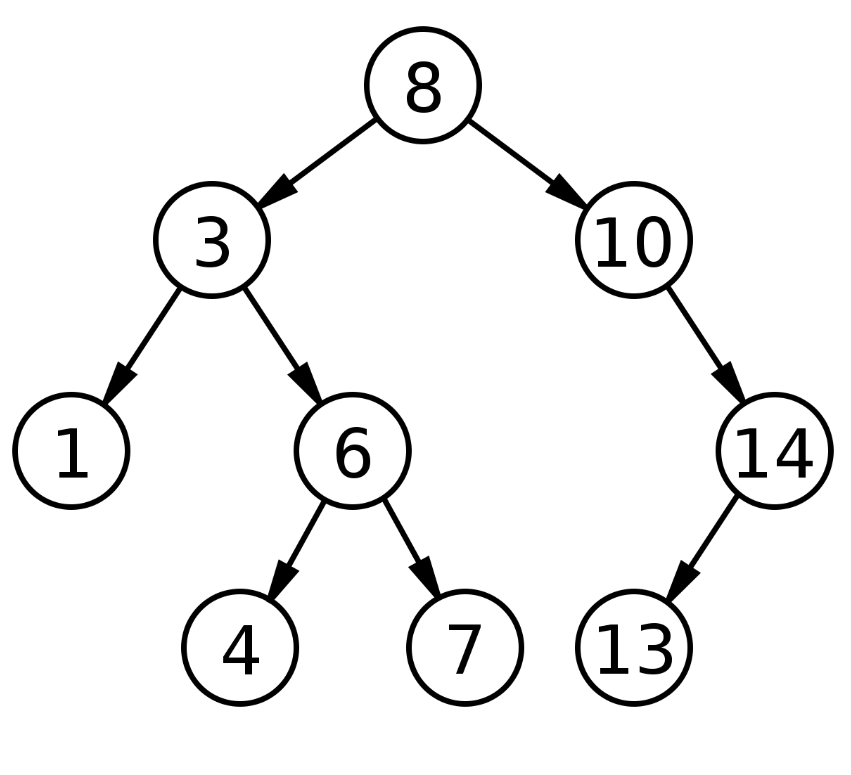
- 이진 탐색과 연결리스트를 결합한 자료구조
(각 장점의 결합)
- 이진 탐색 : 탐색 시간 복잡도 O(log n)
- 연결리스트 : 삽입/삭제 시간 복잡도 O(1)
- 부모의 키가 왼쪽 자식 노드의 키보다 큼
- 부모의 키가 오른쪽 자식 노드의 키보다 작음
- 시간 복잡도 : O(log n) - O(h)
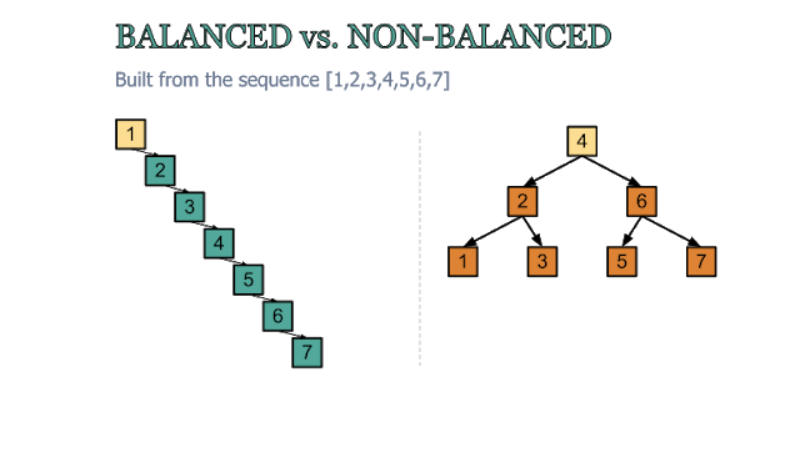
- 저장 순서에 따라 계속 한쪽으로 노드가 추가된다면 왼쪽 그림과 같은 편향 트리가 될 수 있는 가능성이 있음
시간 복잡도 : O(log n) → O(n)
- 트리의 균형을 잡기 위한 자료구조인 Rebalancing 등장하며, 대표적으로 Red-Black Tree가 있음
🔸 B Tree
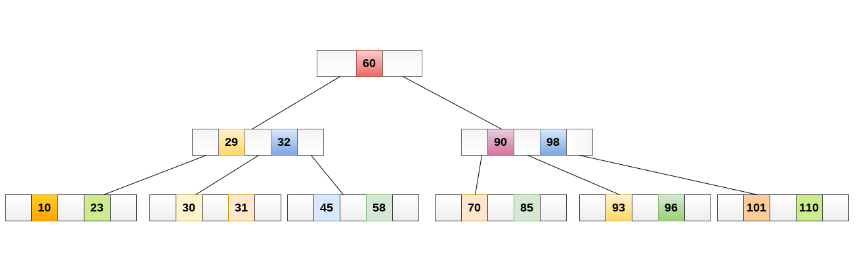
- 자식 노드의 개수가 2개 이상인 트리
- 탐색, root 노드부터 하향식으로 탐색
- 삽입시, 노드 분할 / 삭제시, 노드 합병
- 최악의 경우에도 시간 복잡도 : O(log n)
🔸 B+ Tree
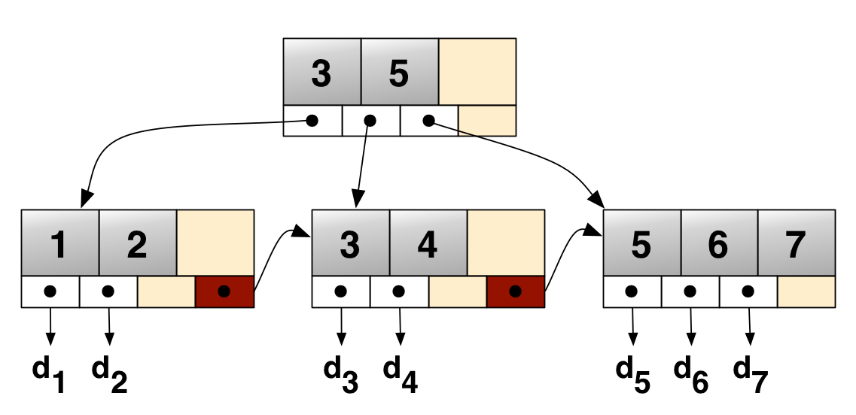
- 특정 키 값이 leaf 노드와 부모 노드에 공존
- 데이터는 leaf 노드에만 존재
- leaf 제외 다른 노드는 인덱스 역할만 수행
- leaf 노드들은 연결리스트 형태로 서로 연결, 오름차순으로 정렬
- 순차 탐색에 효율적
🔸 Red-Black Tree
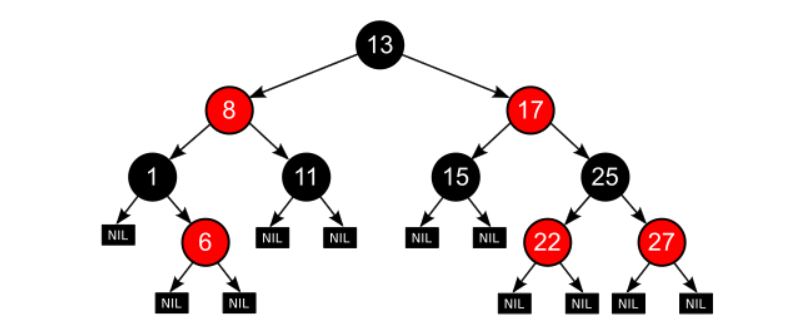
- RBT는 BST의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해 만들어진 자료구조
- 다음 성질을 만족하는 BST
- 각 노드는 Red or Black 이라는 색을 가짐
- Root node의 색깔은 Black
- leaf node는 black
- 어떤 노드의 색이 red라면 두 개의 children 색은 모두 black
- red 노드가 연속으로 2번 나타내면 X
- 모든 leaf 노드에서 black depth는 같다.
- 리프노드에서 루트 노드까지 가는 경로에서 만나는 black 노드의 개수가 같다
✅ Binary Heap
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
- 여러 개의 값들 중에 최대/최소값을 빠르게 찾아내도록 만들어진 자료구조
- 최대힙과 최소힙
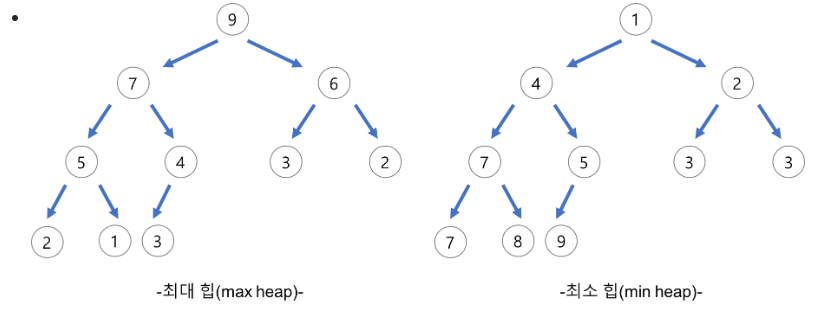
최대힙
- 각 노드의 값이 해당 children의 값보다 크거나 같은 완전 이진 트리
- Root 노드가 최댓값 - 최댓값을 찾는 시간 복잡도 : O(1)
최소힙
- 각 노드의 값이 해당 children의 값보다 작거나 같은 완전 이진 트리
- 최소값을 찾는 시간 복잡도 : O(1)
구현
- 힙을 저장하는 자료구조는 배열!
- 구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용 X
삽입/삭제
삽입
- 힙에 새로운 요소가 들어오면 새로운 노드를 힙의 마지막 노드에 삽입
- 새로운 노드를 부모 노드들과 교환
삭제
- 루트 노드를 삭제하면, 삭제된 루트 노드 자리에 힙의 마지막 노드가 들어감
- 힙을 재구성
- 시간 복잡도 : O(log n)
✅ Hash Table
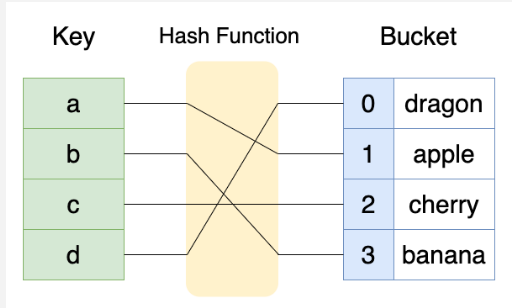
- key를 활용해 검색과 저장이 아주 빠르게 진행되는 자료구조
- key/value 쌍으로 데이터에 접근
- 검색/저장 시간 복잡도 : O(1)
- 해시 충돌로 인한 최악의 경우 : O(N)
hash function
- 데이터의 key값을 배열의 인덱스인 정수로 변환하기 위한 과정 필요
- Collision을 최소화 하는 방향으로 설계
- Collision 해결 방법
Open Address (개방주소법)
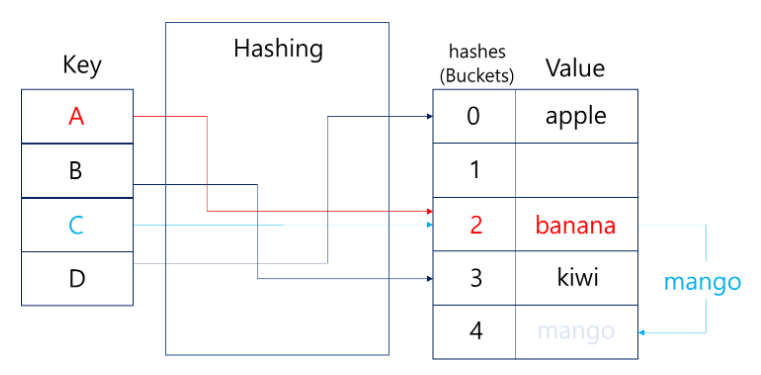
- 충돌이 발생하면 비어있는 다른 버킷을 찾는 방법
- 선형탐색, 이차탐색 등을 사용
- 군집화 발생 가능성이 있음 → 성능 저하
Separate Chaining (체이닝)
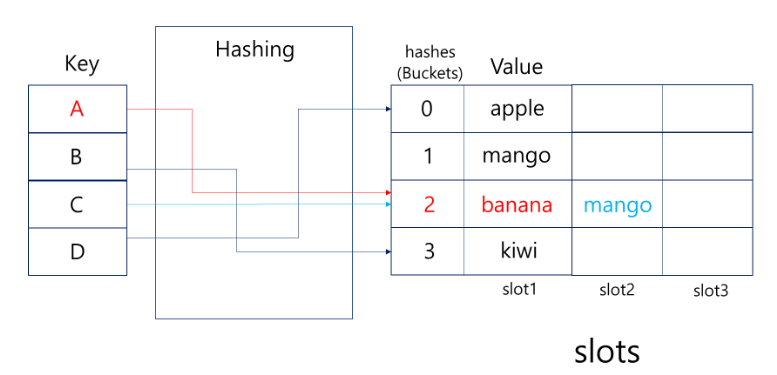
- 충돌이 일어났을 때 동일 slot에 연결 리스트 저장
- 연결 리스트를 사용해 자료들이 계속 연결되는 쏠림 현상이 검색 효율을 낮출 수 있음
- 사용하지 않은 slot 발생 가능성 → 공간 낭비 발생
✅ Graph
- 노드(정점)와 간선을 하나로 모아놓은 자료구조
- 방향 그래프, 무방향 그래프
- 사이클이 가능하고(순환/비순환), 자체 간선도 가능
- 부모 자식 개념 X
그래프 탐색
- 깊이 우선 탐색 (DFS)
- 연결되어 있는 한 정점으로만 나아가다가 더이상 연결되지 않으면 그 전 단계의 정점으로 돌아가는 방법이다.
- 너비 우선 탐색 (BFS)
- 연결되어 있는 모든 정점으로 나아가는 방법이다.
- 시간 복잡도 : O(V+E)
- 최단경로
Minimum Spanning Tree
- 간선 가중치의 합이 최소인 spanning tree
- 모든 정점이 사이클 없이 연결된 형태
Kruskal Algorithm
- 간선 없이 정점들로만 구성된 그래프
- 가중치가 가장 작은 간선부터 검토
- 그래프에 사이클이 생기지 않은다면 추가
- 사이클 생성 여부 판단
- 정점에 set-id 부여
- 연결시 set-id를 하나로 통일
Prim Algorithm
- 한 개의 정점으로 이루어진 초기 그래프
- 가중치가 작은 간선을 통해 연결되는 정점 추가
- 모든 정점이 연결되면 종료









