개요

프로젝트에서 지도 API를 사용해 지도 관련 기능 구현(현재 위치 마커 표시, 길찾기 등) 중 API를 사용하지 않고 직접 출발지와 도착지의 거리를 계산하기 위해 기본적인 거리계산 알고리즘 3개를 기록하고 복습했다.

두 점 사이의 거리를 계산하는 함수에는 여러 가지 방법이 있다. 가장 일반적인 세 가지는 유클리드 거리, 맨해튼 거리, 그리고 하버사인 공식이다.

1. 유클리드 거리 (Euclidean Distance)
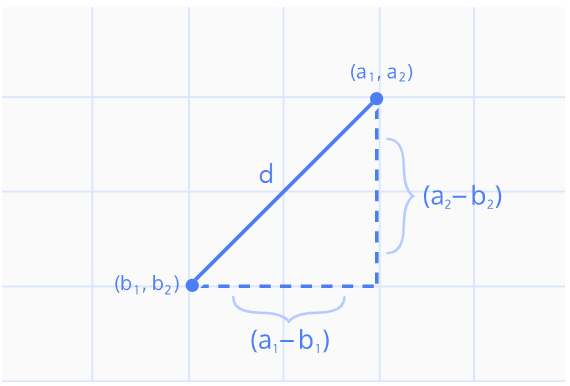
   유클리드 거리는 두 점 사이의 직선 거리를 계산한다. 이 방법은 주로 평면 좌표계에서 사용된다.

python code

import math

def euclidean_distance(lon1, lat1, lon2, lat2):
    return math.sqrt((lon2 - lon1)**2 + (lat2 - lat1)**2)

유클리드 거리 공식

두 점 (x1,y1)와 (x2,y2) 사이의 유클리드 거리는 다음과 같이 계산된다:

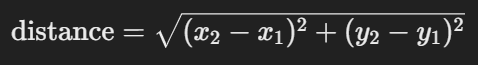
3차원 공간에서는 다음과 같이 z좌표도 계산한다:

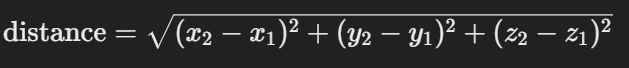
유클리드 거리 계산 단계

1. 두 점의 각 좌표의 차이를 구합니다.
2. 차이의 제곱을 계산합니다.
3. 제곱한 값을 모두 더합니다.
4. 더한 값의 제곱근을 구합니다.

예제 사용

distance = euclidean_distance(1, 2, 4, 6)
print("Euclidean Distance:", distance)
3차원 예제
3차원 공간에서 두 점 (1, 2, 3)과 (4, 6, 8) 사이의 유클리드 거리를 계산해 보겠습니다.

1. 각 좌표의 차이:

x 좌표의 차이: 4 - 1 = 3

y 좌표의 차이: 6 - 2 = 4

z 좌표의 차이: 8 - 3 = 5

2. 차이의 제곱:

3^2 + 4^2 + 5^2

3. 제곱한 값을 더함:

9+16+25=50

4. 더한 값의 제곱근을 구함:

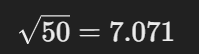
3차원 유클리드 거리 파이썬 코드

def euclidean_distance_3d(x1, y1, z1, x2, y2, z2):
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2 + (z2 - z1)**2)

2. 맨해튼 거리 (Manhattan Distance)
   맨해튼 거리는 두 점 사이의 거리를 수직 및 수평 축으로만 이동하여 계산합니다. 이는 그리드 기반의 도시 거리 계산에 유용합니다.

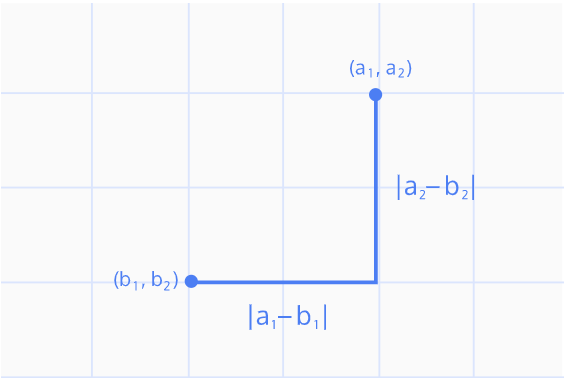
def manhattan_distance(lon1, lat1, lon2, lat2):
    return abs(lon2 - lon1) + abs(lat2 - lat1)

3. 하버사인 공식 (Haversine Formula)
   하버사인 공식은 구의 두 점 사이의 대원 거리를 계산하는 방법입니다. 이는 지구상의 두 지점 간의 거리를 계산하는 데 매우 유용합니다.

import math

def haversine(lon1, lat1, lon2, lat2):
R = 6371.0 # 지구의 반지름 (킬로미터)
lon1, lat1, lon2, lat2 = map(math.radians, [lon1, lat1, lon2, lat2])
dlon = lon2 - lon1
dlat = lat2 - lat1
a = math.sin(dlat / 2)2 + math.cos(lat1) math.cos(lat2) math.sin(dlon / 2)2
c = 2 math.atan2(math.sqrt(a), math.sqrt(1 - a))
distance = R c
return distance

예제 사용

distance = haversine(126.9780, 37.5665, 129.0756, 35.1796)
print("Haversine Distance:", distance)

4. 빈센트 공식 (Vincenty Formula)
   빈센트 공식은 지구를 타원체로 가정하여 두 점 사이의 거리를 계산하는 보다 정밀한 방법입니다. 그러나 구현이 더 복잡합니다.

import geopy.distance

def vincenty_distance(lon1, lat1, lon2, lat2):
coords_1 = (lat1, lon1)
coords_2 = (lat2, lon2)
return geopy.distance.distance(coords_1, coords_2).km

예제 사용

distance = vincenty_distance(126.9780, 37.5665, 129.0756, 35.1796)
print("Vincenty Distance:", distance)