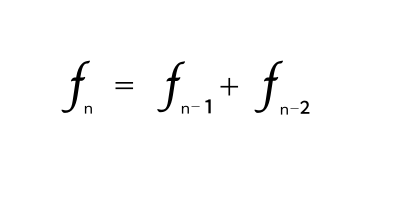[기초수학] 시그마_계차 수열_피보나치 수열_군 수열

✏️시그마 ∑

• 수열의 합을 나타내는 기호
  

✏️계차 수열

• 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열
  

---

계차 수열 : 문제 풀이

✏️피보나치 수열

1, 2번째 수가 1일 경우 Fn=Fn-1+Fn-2

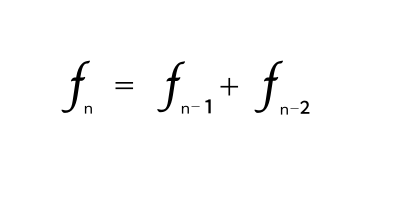
✍️실습

재귀함수 이용

def fibonacci(n): #재귀함수 이용 
    if n == 1 or n == 2:
        return 1

    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

반복문 이용

def fibonacci2(n):
    preN1 = 1
    preN2 = 1
    nowN = 1
    sum = 0

    for i in range(1, n + 1):
        if i == 1 or i == 2:
            nowN = 1
        else:
            nowN = preN1 + preN2
            preN2 = preN1
            preN1 = nowN

        sum += nowN

    print(f'{n}번째 값 : {nowN}')
    print(f'{n}번째 까지의 값 : {sum}')


n = int(input('n 입력 : '))
fibonacci2(n)

✏️팩토리얼

• 1부터 양의 정수 n까지의 정수를 모두 곱한 것

def factorial(n):
    if n == 1:
        return 1

    else:
        return n * factorial(n - 1)

라이브러리 모듈 이용

n = int(input('n 입력 : '))
print(f'{n} 팩토리얼 : {math.factorial(n)}')

✏️군수열

• 여러 개의 항을 묶었을 때 규칙성을 가지는 수열

✍️실습

n번째 항의 값 출력 [정수]

def groupSequence(num):
    # cnt = (n * (n ** 2)) / 2  # n번째 군 까지의 항 개수

    isFlag = True
    cnt = 1
    n = 1
    while isFlag:
        for i in range(1, n + 1):

            if cnt == num:
                print(f'{i}', end='')
                print(f'\n{n}번째 항 : {i}')
                isFlag = False
                break
            else:
                if i == n:
                    print(f'{i}', end='')
                else :
                    print(f'{i}, ', end='')


            cnt += 1

        print()
        n += 1


n = int(input('n항 입력 : '))
groupSequence(n)


💡result

n항 입력 : 50
1
1, 2
1, 2, 3
1, 2, 3, 4
1, 2, 3, 4, 5
1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6, 7
1, 2, 3, 4, 5, 6, 7, 8
1, 2, 3, 4, 5, 6, 7, 8, 9
1, 2, 3, 4, 5
10번째 항 : 5

n번째 항의 값 출력 [분수]

def groupSequence2(num):
    # cnt = (n * (n ** 2)) / 2  # n번째 군 까지의 항 개수

    isFlag = True
    cnt = 1
    n = 1
    while isFlag:
        for i in range(1, n + 1):

            if cnt == num:
                print(f'{i}/{n + 1 - i}', end='')
                print(f'\n{num}번째 항 : {i}/{n + 1 - i}')
                isFlag = False
                break
            else:
                if i == n:
                    print(f'{i}/{n + 1 - i}', end='')
                else:
                    print(f'{i}/{n + 1 - i}, ', end='')

            cnt += 1

        print()
        n += 1


n = int(input('n항 입력 : '))
groupSequence2(n)

💡result
n항 입력 : 25
1/1
1/2, 2/1
1/3, 2/2, 3/1
1/4, 2/3, 3/2, 4/1
1/5, 2/4, 3/3, 4/2, 5/1
1/6, 2/5, 3/4, 4/3, 5/2, 6/1
1/7, 2/6, 3/5, 4/4
25번째 항 : 4/4