고지마 히로유키 - 세상에서 가장 쉬운 통계학 입문
💡 통계학이란 무엇인가? 기술통계와 추리통계
통계학은 크게 두 부분으로 이루어져 있다. 하나는 '기술 통계'라고 부르는 부분이고, 또 하나는 '추리 통계' 라고 부르는 부분이다.
기술 통계 : 관측을 통해 얻은 데이터에서 그 데이터의 특징을 뽑아내기 위한 기술
- 기원이 상당이 오래됨 : 확실한 기원은 17세기
- 도수분포표, 히스토그램 등 표와 그래프로 표현하는 방법론
- 평균값이나 표준편차 같은 통계량으로 표현 하는 방법론
- 사회나 경제 상황 파악, 기상이나 해양 등 환경 조사 등
추리 통계 : 통계학 방법과 확률 이론을 섞은 것으로 '전체를 파악할 수 없을 정도의 큰 대상' 이나 '아직 일어나지 않은, 미래에 일어날 일' 에 관해 추측하는 것
- 20세기에 확립된 이론
- 부분에서 전체를 추측한다는 의미
- 선거 개표시 당선 예측, 주가 예상, 금융상품이나 보험 상품의 가격 책정 등
💡 도수분포표와 히스토그램
데이터를 다영한 수치로 나타내는 것을 '분포' 라고 한다.
분포의 특징이나 반복되는 것을 이끌어내기 위한 방법을 '통계' 라고 한다
통계에서 사용되는 것은 '축약' 이라고 부르는 방법이다.
축약은 '데이터로 나열되어 있는 많은 숫자를 어떤 기준으로 정리정돈해서 의미있는 정보만 추출' 하는 것을 의미하는 말로, 크게 다음과 같은 두 가지 방법이 있다.
- 그래프로 만들어서 그 특징을 파악할 수 있도록 한다.
- 숫자 하나로 특징을 대표하도록 한다.
이 대표하는 숫자를 '통계량' 이라고 한다.
💡도수분포표 만들기
데이터 자체를 만들 때 가장 많이 쓰이난 그래프는 '히스토그램' 으로, 쉽게 말하면 '막대그래프' 다. 이것을 만들기 위해서는 먼저 도수분포표라는 표를 만들어야 하는데, 만드는 방법은 다음과 같다.
- 데이터 중에서 수치가 가장 큰 것과 가장 작은 것을 찾습니다.
- 최대값부터 최소값까지 포함되도록 하여 구간을 자르기 좋은 대강의 범위를 만들고, 그 범위 내에서 5~8개 정도의 작은 범위들로 자릅니다.
- 각 계급을 대표하는 수치를 정합니다. 일반적으로는 해당 계급의 범위 중간값을 선택합니다. 이를 '계급값'이라고 합니다.
- 각 계급에 속하는 데이터의 개수를 세어 '도수'를 구합니다.
- 각 계급의 도수가 전체 데이터에서 차지하는 비율을 계산하여 '상대도수'를 구합니다. 상대도수는 합하면 1이 됩니다.
- 각 계급의 도수를 누적하여 '누적도수'를 계산합니다. 최종 누적도수는 데이터의 총 개수와 일치합니다.
✍️예제
# 여대생 80명의 키(cm)
151 154 158 162
154 152 151 167
...
169 162 162 156
150 153 143 156
- 최대값은 169이고 최소값은 143 이다.
- 140 에서 170까지를 범위로 하는 계급을 만든다. 그리고 데이터는 5개씩 묶으면 6개의 계급이 생긴다.
- 계급값으로는 가장 가운데 값을 사용한다. 예를 들어서 제 1계급에서는 141, 142, 143, 144, 145 의 중 중간값인 143을 대표값으로 선택한다.
- 각 계급에 들어가 있는 총 개수(도수) 를 센다.
- 각 도수를 데이터의 총 개수 80으로 나눠서 상대도수를 구한다.
- 도수를 위에서부터 차례로 더해 내려가며 누적도수를 계산한다.
| 계급 | 계급값 | 도수 | 상대도수 | 누적도수 |
|---|---|---|---|---|
| 141-145 | 143 | 1 | 0.0125 | 1 |
| 146-150 | 148 | 6 | 0.075 | 7 |
| 151-155 | 153 | 19 | 0.2375 | 26 |
| 156-160 | 158 | 30 | 0.375 | 56 |
| 161-165 | 163 | 18 | 0.225 | 74 |
| 166-170 | 168 | 6 | 0.075 | 80 |
우선, 중요한 것은 이렇게 도수분포표를 만들면 잃어버리는 정보가 있다는 점이다. 바로 '데이터에 나타나 있던 수치들 자체' 다.
예를 들어, 도표 1-2의 제4계급인 156부터 160까지의 범위를 보면. 도수를 통해 30개의 데이터가 있다는 것을 알 수 있지만, 그 30개의 데이터의 세부적인 수치는 알 수 없다.
하지만 이런 희생을 감수하는 대신에 귀중한 정보를 얻을 수 있다. 도수 칸을 보면 키가 작은 계급부터 차례대로 1, 16, 19, 30, 18, 6 이란 수치가 나와 있는데, 이 수치로 다음과 같은 데이터의 특징을 발견할 수 있다.
- 특징1 : 키는 균등하게 분포하지 않고, 어느 한곳에 집중되어 있다.
- 특징2 : 집중되어 있는 곳을 기점으로 삼으면, 이 기점으로부터 작은 편에 속하든지 큰 편에 속하는 추이를 보인다. 즉 데이터의 분포에는 '어느 한 곳을 축으로 좌우 대칭성이 있다는 말이다.'
성인 여성들의 키에대한 특징을 정리하면
- 어떠한 수치든지 가능한 것은 아니다.
- 어느 한 키(158cm) 주변에 집중되어 있다.
- 그곳(158cm)을 기점으로 해서 큰 편과 작은 편은 '수치가 별로 보이지 않는다는 점이 서로 비슷하다'
이러한 특징들은 데이터 자체를 그냥 보았을 때는 몰랐던 정보다. 축약은 데이터의 세부적인 수치들을 희생시키지만, 이 희생으로 데이터의 분포와 그 이면에 있는 특징들이 돋보이게 된다.
💡히스토그램 만들기
- 가로축에 계급값을 같은 간격으로 둔다
- 각 계급위에 만대를 세우는데, 막대 높이는 그 계급값에 속란 계급 도수로 한다.
이렇게 만든 막대그래프를 히스토그램 이라고 한다.
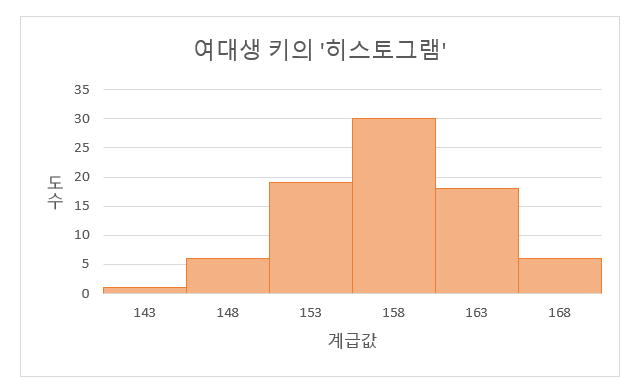
이 히스토그램을 보면 앞에서 도수분포표를 통해 알게 된 특징을 더욱 명확하게 알 수 있다.
막대의 높이는 가운데 세 막대가 높고 양쪽 바깥의 막대는 낮다. 데이터 분포가 좌우대칭에 가까운 특성도 찾아볼 수 있다.
위 히스토그램을 보고 '정확히 키가 158cm인 여대생이 30명 있다' 이렇게 해석하면 현실을 정확하게 나타낼 수는 없지만 여기서 우리는 '데이터에 잠재되어 있는 특징' 을 알 수 있다.
📌정리
- 데이터 자체는 현실 그대로를 나타내지만, 이것을 아무리 자세히 본다고해도 알 수 있는 것은 없다.
- 데이터를 축약하는 방법에는 '그래프' 를 만드는 방법과 '통계량'을 구하는 방법 두 가지가 있다.
- 도수분포표는 데이터를 5~8개 정도의 그룹으로 나눈 것이다. 도수분포표로 데이터의 특성을 파악할 수 있다.
- 히스토그램이란 도수분포표를 그래프로 바꾼 것으로 , 더욱 쉽게 데이터의 특징을 파악할 수 있다.
