[통계학 입문] 표준편차 1

고지마 히로유키 - 세상에서 가장 쉬운 통계학 입문

---

표준편차로 데이터의 특수성 평가

표준편차를 통해 알수 잇는 것

• 한 데이터 세트 중에 있는 어떤 데이터 하나의 수가 갖는 의미
• 여러 데이터 세트들을 서로 비교해서 나타나는 차이

표준편차 예시

💡시험성적

만약 내가 75점을 맞은 시험의 평균이 60점이라면 나는 얼마나 잘 본 것일까?

물론 평균보다 높은 점수이기 떄문에 나쁘지않은 성적일것이다. 얼마나 잘 본지 파악하기 위해서는 표준편차를 알아야한다.

표준편차 즉, '평균값에서 떨어진 수만큼을 평균화한 값'이 12점 일 때 나의 편차 15와 표준편차를 비교하면 나는 평균 보다 잘한 쪽에서 '보통'이 된다.

반대로 표준 편차가 8점이면 나는 표준편차의 2배 정도나 멀리 떨어져 있으므로 평균 보다 잘한 쪽에서도 '높은' 성적이 된다.

📌 표준편차가 12점인 경우

약 표준편차의 1배 떨어져 있음 : 보통 성적

|-----|-----|-----|----|
           60    72   75(나)
          avg   std   

📌 표준편차가 8점인 경우

약 표준편차의 2배정도 멀리 떨어져 있음 : 좋은 성적

|-----|-----|----|------|
           60   68   75(나)
          avg  std   

어떤 하나의 데이터가 가진 특수성은 평균에서 떨어진 정도를 나타내는 수치만으로는 알 수 없고, 표준 편차를 기준으로 가정해야만 알 수 있다.

즉, 이것은 {(데이터)-(평균값)}$\div$(표준편차) 라는 계산을 기준으로 데이터를 평가하는 것이다.

데이터의 특수성 평가기준

데이터 세트 중에 있는 어느 한 데이터의 편차가 표준편차로 계산해서 $\pm1$배 전후라면 이것은 '평범한 데이터' 라고 할 수 있으며, $\pm2$배 멀리 있는 데이터일 경우 '특수한 데이터' 라고 할 수 있다.

특수성 이란?

데이터 전체 성질이 정규분포에 가깝다고 한다면, 평균값에서 표준편차 $\pm1$배의 범위 내에 약 70%의 데이터가 들어간다고 생각하면 된다.

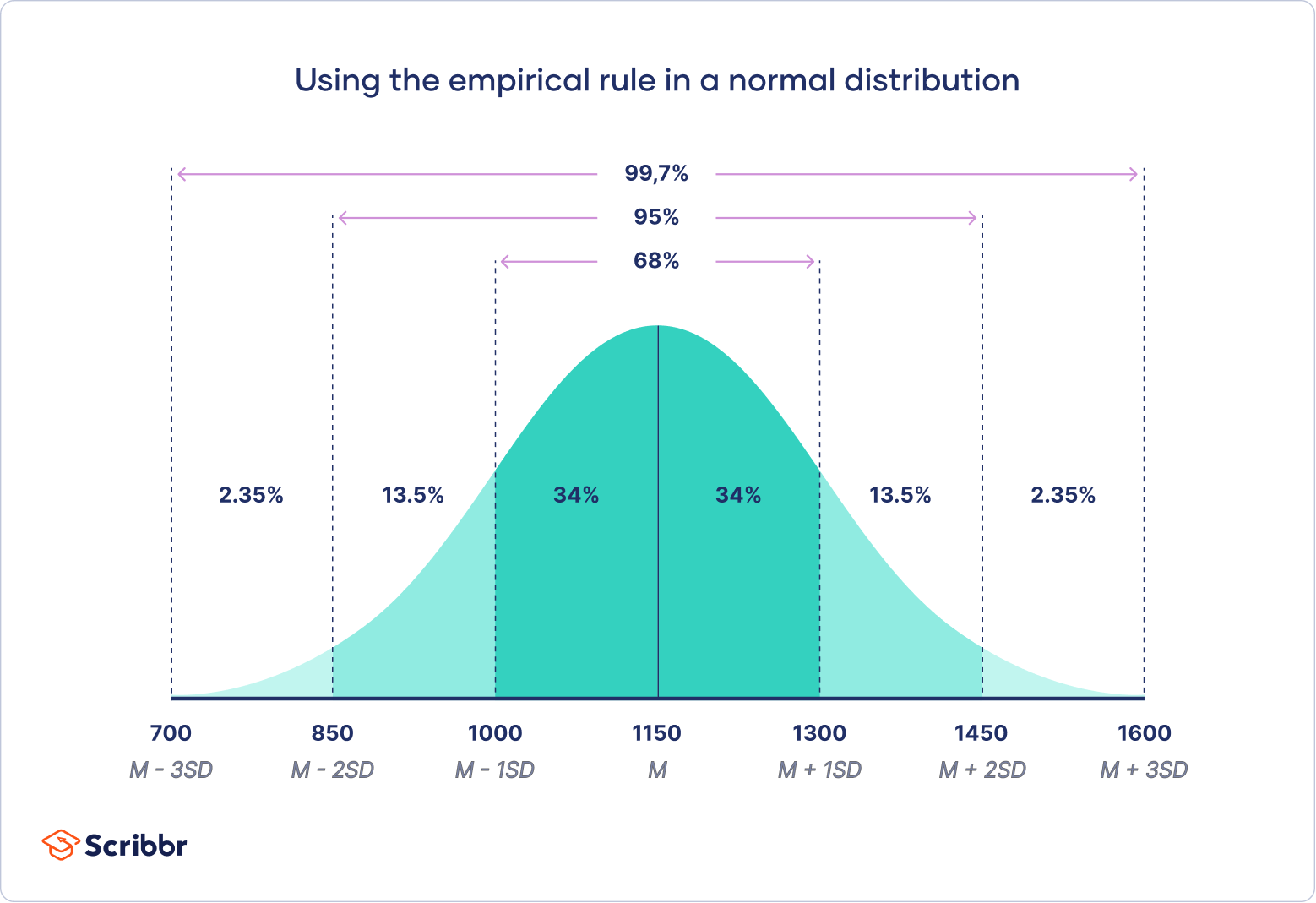
Image by Normal Distribution | Examples, Formulas, & Uses

또한 표준편차 $\pm2$배보다 멀리 떨어진 데이터는 좌우 양쪽을 합쳐 대략 5%밖에 없다고 생각하면 된다.

가공된 데이터의 평균값과 표준편차

기본 데이터 X

X : [1, 3, 4, 5, 7]
X의 평균 : 4.0
X의 편차 : [-3.0, -1.0, 0.0, 1.0, 3.0]
X의 분산 : 4.0
X의 표준편차 : 2.0

📌 데이터에 일정한 수를 더하는 가공의 효과

X $+$ 4 : [5, 7, 8, 9, 11]
X $+$ 4 의 평균 : 8.0
X $+$ 4 의 편차 : [-3.0, -1.0, 0.0, 1.0, 3.0]
X $+$ 4 의 분산 : 4.0
X $+$ 4 의 표준편차 : 2.0

X 데이터의 모즌 수에 일정한 수 a를 더해서 새로운 데이터 Y를 만들면, Y 데이터의 평균값은 X데이터의 평균값에 a를 더한 것이 되며 분산과 표준편차는 X데이터와 동일하다.

📌 데이터에 일정한 수를 곱하는 가공의 효과

X $\times$ 4 : [4, 12, 16, 20, 28]
X $\times$ 4 의 평균 : 16.0
X $\times$ 4 의 편차 : [-12.0, -4.0, 0.0, 4.0, 12.0]
X $\times$ 4 의 분산 : 64.0
X $\times$ 4 의 표준편차 : 8.0

X 데이터의 모즌 수에 일정한 수 k를 곱해서 새로운 데이터 Y를 만들면, Y 데이터의 평균값은 X데이터의 평균값에 k를 곱한 것이 되며 분산은 k의 제곱배, 표준편차는 k배가 된다.

💡{(데이터)$-$(평균값)} $\div$ (표준편차)

• 데이터 - 평균값이라는 것은 각 데이터의 수에 평균값을 뺀 것이기 때문에 그 평균값은 0이 되며 표준편차는 동일하다.

• 다음으로 각 데이터의 수를 표준편차로 나눈다는 것은 표준편차의 역수 $\frac{1}{표준편차}$ 를 곱하기 때문에 평균은 0 * $\frac{1}{표준편차}$ = 0 이 되며, 표준 편차는 표준편차 $\times$ $\frac{1}{표준편차}$ = 1 이 된다.