Node와 Edge로 이루어진 자료구조
Tree의 특성을 이해하자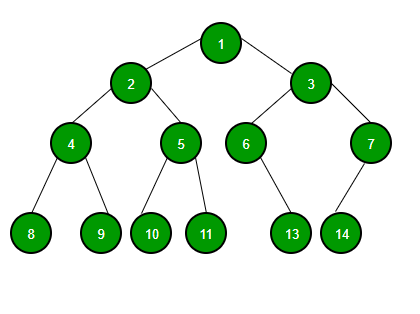
트리는 값을 가진 노드(Node)와 이 노드들을 연결해주는 간선(Edge)으로 이루어져있다.
그림 상 데이터 1을 가진 노드가 루트(Root) 노드다.
모든 노드들은 0개 이상의 자식(Child) 노드를 갖고 있으며 보통 부모-자식 관계로 부른다.
아래처럼 가족 관계도를 그릴 때 트리 형식으로 나타내는 경우도 많이 봤을 것이다. 자료구조의 트리도 이 방식을 그대로 구현한 것이다.

트리는 몇 가지 특징이 있다.
- 트리에는 사이클이 존재할 수 없다. (만약 사이클이 만들어진다면, 그것은 트리가 아니고 그래프다)
- 모든 노드는 자료형으로 표현이 가능하다.
- 루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.
- 노드의 개수가 N개면, 간선은 N-1개를 가진다.
가장 중요한 것은, 그래프와 트리의 차이가 무엇인가인데, 이는 사이클의 유무로 설명할 수 있다.
사이클이 존재하지 않는 그래프라 하여 무조건 트리인 것은 아니다 사이클이 존재하지 않는 그래프는 Forest라 지칭하며 트리의 경우 싸이클이 존재하지 않고 모든 노드가 간선으로 이어져 있어야 한다
## 트리
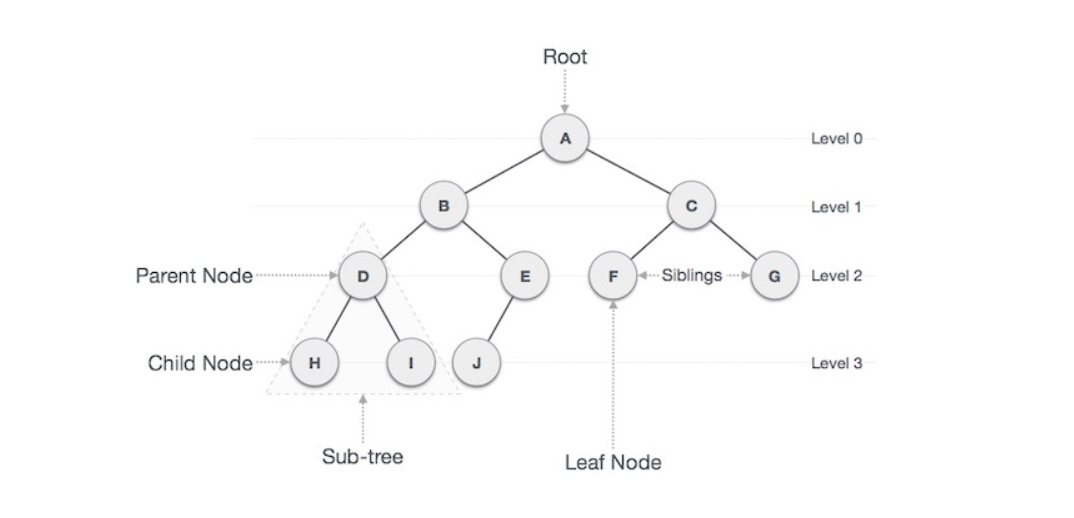
노드 (Node)
트리를 구성하고 있는 기본 요소
노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있음.
A, B, C, D, E, F, G, H, I, J
간선 (Edge)
노드와 노드 간의 연결선
루트 노드 (Root Node)
트리 구조에서 부모가 없는 최상위 노드
root node : A
부모 노드 (Parent Node)
자식 노드를 가진 노드
H, I에 부모 노드는 D
자식 노드 (Child node)
부모 노드의 하위 노드
노드 D의 자식 노드는 H, I
형제 노드 (Sibling node)
같은 부모를 가지는 노드
H, I는 같은 부모를 가지는 형제 노드
외부 노드(external node, outer node), 단말 노드 (terminal node), 리프 노드(leaf node)
자식 노드가 없는 노드
H, I, J, F, G
내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node)
자식 노드 하나 이상 가진 노드
A, B, C, D, E
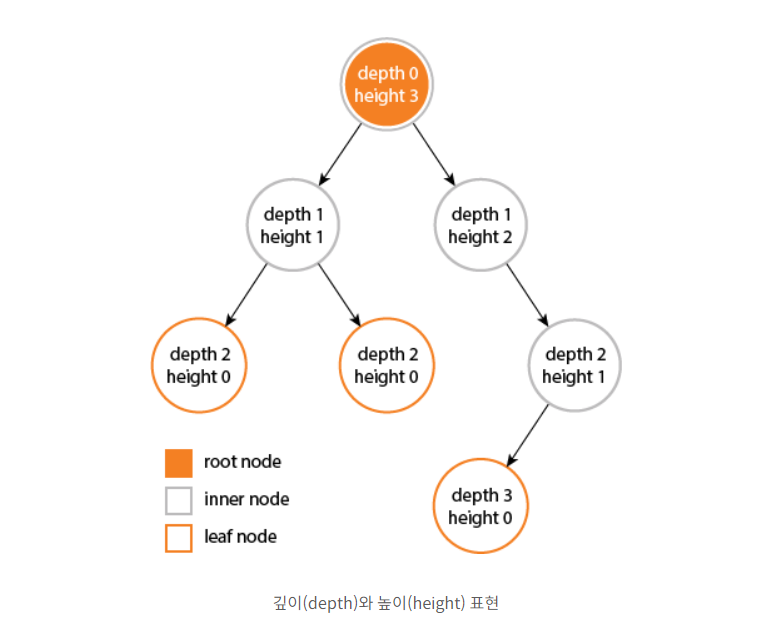
깊이 (depth)
루트에서 어떤 노드까지의 간선(Edge) 수
루트 노드의 깊이 : 0
D의 깊이 : 2
높이 (height)
어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
리프 노드의 높이 : 0
A 노드의 높이 : 3
Level
루트에서 어떤 노드까지의 간선(Edge) 수
Degree
노드의 자식 수
Leaf node의 degree : 0; A의 degree : 2
Path
한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
A & H 경로 : A-B-D-H
Path Length
해당 경로에 있는 총노드의 수
A & H 경로 길이 : 4
Size
자신을 포함한 자손의 노드 수
노드 B의 size : 6
Width
레벨에 있는 노드 수
Level 2 width : 4
Breadth
리프 노드의 수
Breadth : 5
Distance
두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
D와 J의 Distance : 3
Order
부모 노드가 가질 수 있는 최대 자식의 수
Order 3 : 부모 노드는 최대 3명의 자식을 가질 수 있다.
트리 순회 방식
트리를 순회하는 방식은 총 4가지가 있다. 위의 그림을 예시로 진행해보자

-
전위 순회(pre-order)
각 부모 노드를 순차적으로 먼저 방문하는 방식이다.
(부모 → 왼쪽 자식 → 오른쪽 자식)
1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14
-
중위 순회(in-order)
왼쪽 하위 트리를 방문 후 부모 노드를 방문하는 방식이다.
(왼쪽 자식 → 부모 → 오른쪽 자식)
8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7
-
후위 순회(post-order)
왼쪽 하위 트리부터 하위를 모두 방문 후 부모 노드를 방문하는 방식이다.
(왼쪽 자식 → 오른쪽 자식 → 부모)
8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1
-
레벨 순회(level-order)
부모 노드부터 계층 별로 방문하는 방식이다.
1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14
Code
public class Tree<T> {
private Node<T> root;
public Tree(T rootData) {
root = new Node<T>();
root.data = rootData;
root.children = new ArrayList<Node<T>>();
}
public static class Node<T> {
private T data;
private Node<T> parent;
private List<Node<T>> children;
}
}