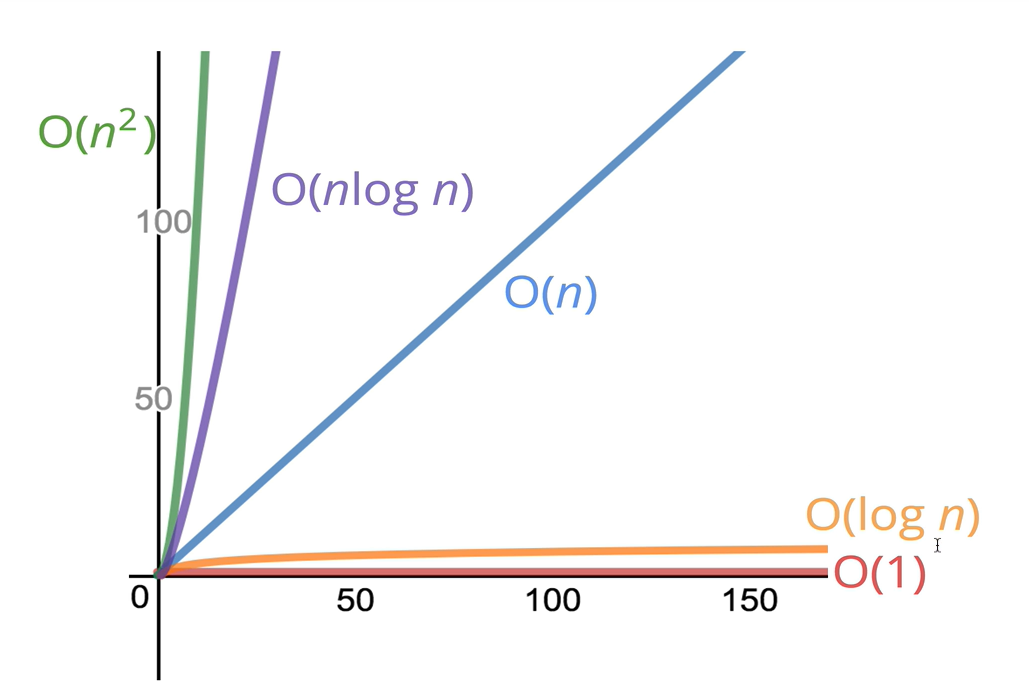
Big-O 표기법
문제 해결을 위한 방법으로 수십개의 해결책이 있는데,
이 많은 해결법중에 어떠한 해결법이 가장 뛰어난지 알 수 있는가?
이러한 여러가지 코드를 서로 비교하고 성능을 평가하는 가장 핵심적인 목표가 Big-O 표기법이라 할 수 있다. 그만큼 알고리즘을 연구할 때, 떼래야 뗄 수 없는 부분이기 때문에 이 부분의 대한 개념을 먼저 숙지하고 넘어가야 할 것이다.
- 정식으로 입력된 내용이 늘어날 수록 알고리즘에 실행 시간이 어떻게 변하는지 설명하는 공식적인 방식
- 대략적으로 숫자를 세는 것의 붙인 공식적인 표현
- 빅오는 어떤 함수의 입력값이 늘어나는 것과 함수 실행 시간이 변하는 관계를 의미
- 오로지 변하는 것의 전반적인 추세에만 주목
- 빅오 표기법에 따른 네가지의 경우의 수

1. 함수의 매개변수값에 비례해서 시간이 늘어나는 경우
- 바로 #1 알고리즘과 같은 경우. input에 따라 걸리는 시간이 비례하여 증가하기 때문에 해당 알고리즘을 사용 할 경우 실행 시간이 오래 걸릴 수 있다.
2. 함수의 매개변수값에 비례해서 시간이 제곱하여 늘어나는 경우
- 해당 알고리즘은 input에 비례해서 시간이 비례해서 증가하기 때문에 해당 알고리즘 사용에 대해서 고려해 볼 필요성이 있다.
3. 함수의 매개변수값에 상관없이 시간이 일정한 경우
- #2 알고리즘 같은 경우. 연산해야 되는 갯수가 매개변수가 증가하더라도 일정하기 때문에 시간 역시 일정하다. 해당 알고리즘을 사용 할 경우 실행 시간이 일정하게 빠를 수 있다.
4. 위의 세가지 경우와 다른 경우
- log 사용 등 다른 방식으로 알고리즘을 사용 한 경우이다.
# 1
function addUpTo(n) {
let total = 0;
for (i = 1; i <= n; i++) {
total += i;
}
return total;
}
addUpTo(n);
# 2
function addUpTo(n) {
return n * (n+1) / 2;
}
addUpTo(n)해당 두 알고리즘의 걸리는 시간을 표로 나타나게 되면
#1 알고리즘

- n이 증가한 양에 비례해서 걸리는 시간 또한 늘어난다.
#2 알고리즘
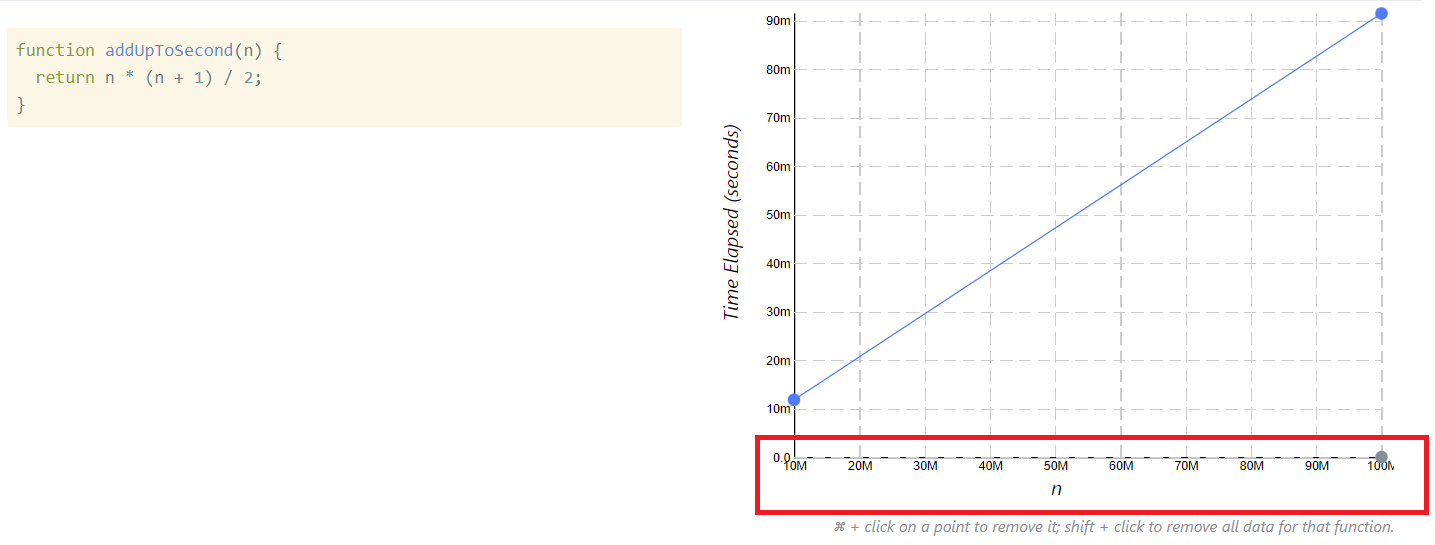
- n이 증가하여도 해당 알고리즘이 실행하는 시간이 비례해서 증가하지 않는다.
즉, #2 알고리즘 함수를 사용했을 때, 실행 시간이 훨씬 짧아 지므로 두번째 알고리즘을 채택하는 것이 바람직!
Another Examples
1. 2*O(n)

- 해당 함수를 살펴보면 for 구문으로 인해 O(n)이 2번 쓰인다. 그래서 2*O(n)으로 n에 비례해 시간이 더욱 증가한다고 생각 할 수 있으나, 결국 큰 틀은 O(n) 이다.
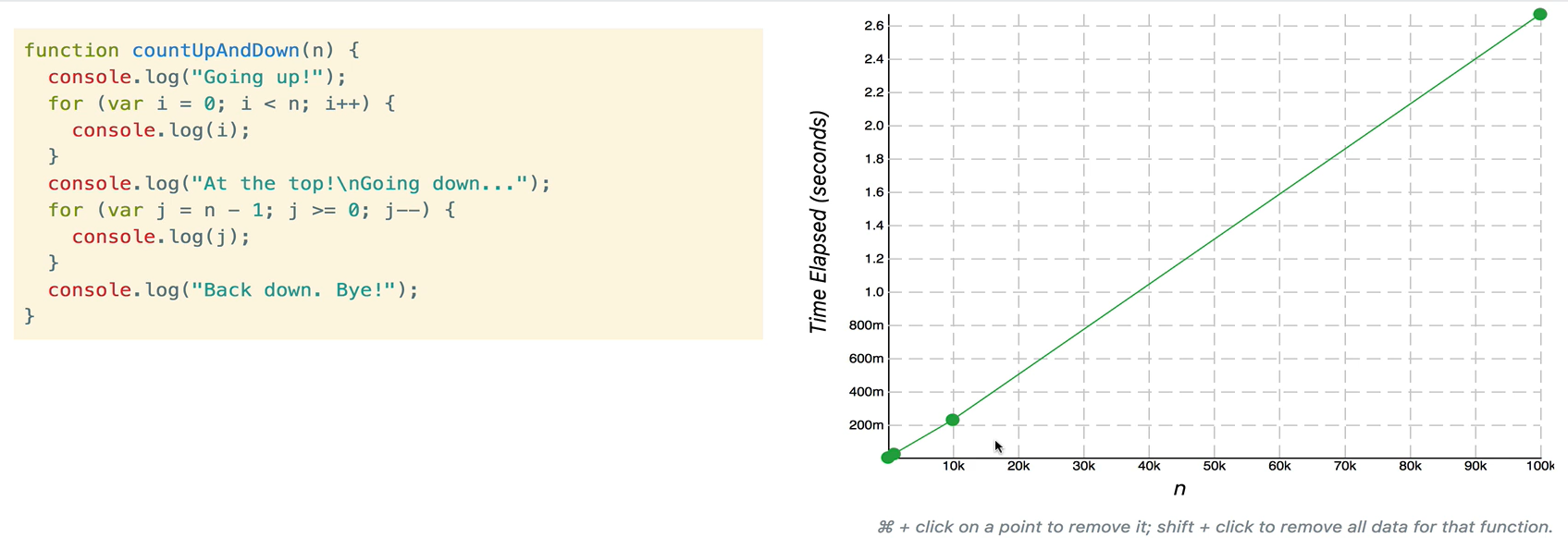
- 해당 그래프를 살펴보면 2*O(n) 역시 매개변수 n에 따라 실행 시간이 일정한 모습을 볼 수 있다.
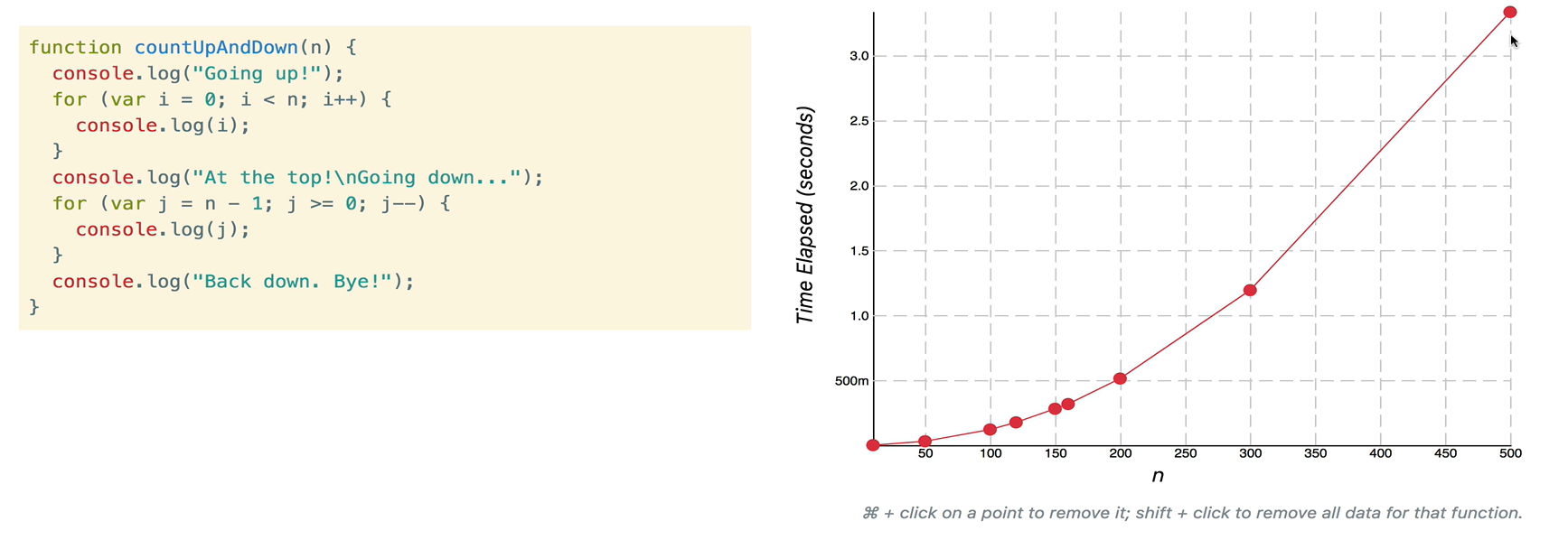
2. O(n2) - N중첩일 경우

- 해당 함수를 살펴보면 for 구문 안에 for 구문이 들어있는 형태로 O(n2)의 형태를 띄게 된다.
따라서 매개변수에 비례해 걸리는 시간이 제곱으로 증가하므로 실행시간이 제곱으로 늘어나게 될 것이다.
빅오 표기법에 따른 그래프 형식