힙(Heap)

힙(Heap)이란?

데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)

• 완전 이진 트리 : 노드를 삽입할 때 최하단 왼쪽 노드부터 차례로 삽입하는 트리

힙을 사용하는 이유

배열에 데이터를 넣고, 최대값과 최소값을 찾으려면 O(n)이 걸림
반면, 힙에 데이터를 넣고 최대값과 최소값을 찾으려면, O(logn)이 걸림
우선순위 큐와 같이 최대값 혹은 최소값을 빠르게 찾아야하는 자료구조 및 알고리즘 구현에 활용

힙(Heap)의 구조

최대 힙(Max Heap)과 최소 힙(Min Heap)으로 분류해볼 수 있음

• 최대 힙(Max Heap) : 부모 노드 >= 자식 노드
• 최소 힙(Min Heap) : 부모 노드 <= 자식 노드

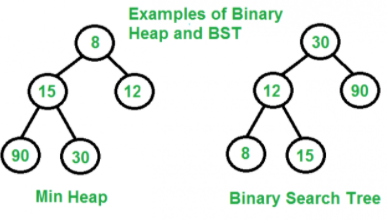
힙 VS 이진 탐색 트리

공통점 :
힙과 이진 탐색 트리는 모두 "이진트리"이다

차이점 :

힙은 최대/최소값 검색을 위한 구조
힙은 각 노드의 값이 자식 노드보다 크거나 같다(Max Heap)
힙은 각 노드의 값이 자식 노드보다 작거나 같다(Min Heap)
힙의 자식 노드 값은 왼쪽이 클 수도 있고, 오른쪽이 클 수도 있음

이진 탐색 트리는 탐색을 위한 구조
이진 탐색 트리는 왼쪽 자식 노드 값이 가장 작고, 그 다음은 부모노드, 그 다음 오른쪽 자식 노드 값이 가장 큼

이미지 출처

힙(Heap)과 배열

일반적으로 힙 구현시 배열 자료구조를 활용
배열은 인덱스가 0번 부터 시작하지만, 0번을 None으로 비워두고 root 노드 인덱스를 1번 으로 지정하면 구현이 좀더 쉬움

부모 노드 인덱스 번호      = 자식 노드 인덱스 번호 // 2
왼쪽 자식 노드 인덱스 번호  = 부모 노드 인덱스 번호 * 2
오른쪽 자식노드 인덱스 번호  = 부모 노드 인덱스 번호 * 2 + 1

이미지 출처