[알고리즘/Python] 동적 프로그래밍(Dynamic Programming)

📌 동적 프로그래밍이란?

동적 프로그래밍(Dynamic Programming)은 어떤 문제를 해결하는 방법 중 하나로, 큰 문제를 작은 하위 문제로 나누어 해결하는 알고리즘 설계 기법입니다. 이러한 하위 문제들은 한 번만 계산하고, 그 결과를 메모리에 저장해두었다가 필요할 때 재사용하여 중복 계산을 피할 수 있습니다. 이를 통해 시간 복잡도를 줄이고 효율적으로 문제를 해결할 수 있습니다.

그렇다면 어떤 문제에 DP를 사용하면 될까요?🧐
두가지의 조건을 만족하는지 확인해보세요!

1. 큰 문제를 작은 문제로 나눌수 있는지?
2. 동일한 작은 문제를 반복적으로 작동시켜야 하는지?

예를 들어서 설명해볼께요. DP 알고리즘의 대표 문제는 피보나치 수열 문제가 있습니다.

피보나치 수를 각각 구해보면 아래와 같습니다:

n	피보나치 수열
0	0
1	1
2	1
3	2
4	3
5	5
6	8

여기서 하나의 규칙을 발견할 수 있습니다. 앞에 있는 두 수를 더하면 피보나치를 수를 구할수 있습니다.이러한 규칙 또는 관계식을 저희는 "점화식"이라고 부르게 됩니다. 피보나치의 점화식을 구하면 다음과 같습니다.

• $A_1=1$ (시작 항)
• $A_2=1$ (시작 항)
• $A_n = A_(n-1)+ A_(n-2)$

피보나치 수열의 규칙을 다르게 나타내면 다음과 같습니다.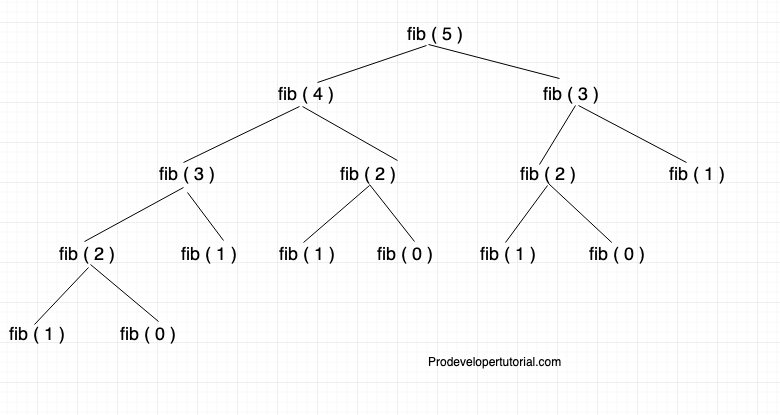

📌 동적 프로그래밍 종류

앞서 언급한 피보나치 수열을 DP로 푸는 방법은 두가지가 있습니다. 동적 프로그래밍은 크게 "탑다운 방식(메모이제이션)"과 "보텀업 방식(테이블 사용)"으로 구현할 수 있습니다.

탑다운 방식(메모이제이션)

• 재귀적으로 큰 문제를 작은 문제들로 나누어 해결하면서, 중간 결과들을 메모리에 저장하여 중복 계산을 피합니다.
• 메모이제이션(memoization)은 계산한 값을 저장하는 캐시를 의미합니다.
• 이미 계산한 하위 문제의 결과를 저장해두고, 같은 하위 문제를 다시 만났을 때 이전에 계산한 결과를 사용합니다.
• 재귀적인 호출로 구현되므로, 스택 오버플로우가 발생할 수 있습니다.

N = int(input())
seq = [0, 1, 1] + [0] * (N - 2)

def fibonacci(x):
    if seq[x]:   
        return seq[x]
    seq[x] = fibonacci(x - 1) + fibonacci(x - 2)
    return seq[x]
print(fibonacci(x))

보텀업 방식(테이블 사용)

• 작은 문제부터 차례대로 해결하면서 결과를 테이블에 저장합니다.
• 작은 문제의 결과를 이용해 큰 문제를 점진적으로 해결합니다.
• 반복문을 사용하여 구현되므로 스택 오버플로우의 위험은 없습니다.
• 보텀업 방식은 일반적으로 더 선호되는 방식입니다.

N = int(input())
seq = [0, 1, 1] + [0] * (N - 2)

def fibonacci(x):
    for i in range(3, x+1):
        seq[i] = seq[i-1] + seq[i-2]
    return seq[x]
print(fibonacci(x))

---

📌 실전 문제

• 프로그래머스 - 문제1
• 프로그래머스 - 문제2