[ML] 10주차-1 : Batch / Stochastic / Mini-batch gradient descent, 학습률

k_dah·2022년 1월 1일

MachineLearning_AndrewNg

목록 보기

29/32

Machine Learning by professor Andrew Ng in Coursera

Gradient Descent with Large Datasets

1) Learning With Large Datasets

학습알고리즘이 이전보다 더 잘 동작하는 이유는 학습알고리즘을 훈련시킬 수 있는 데이터셋이 커졌기 때문이다.
데이터셋이 커지면 왜 성능이 좋아질까?

Machine learning and data

이전에 배웠던 성능이 좋은 학습 알고리즘을 얻는 방법 중 하나는 low bias 알고리즘을 크기가 큰 데이터셋으로 훈련시키는 것이었다.

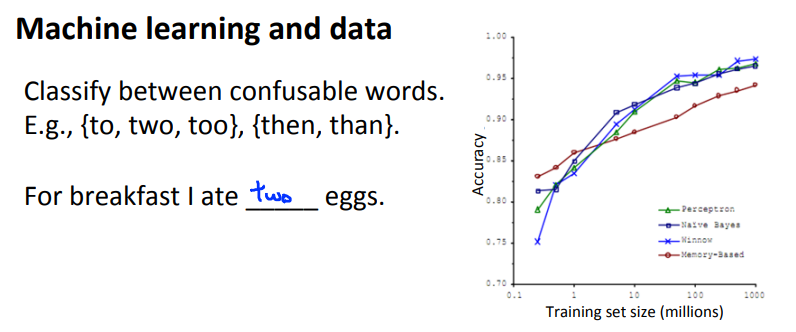
Learning with large datasets

크기가 큰 데이터셋으로 학습할 때에 연산비용과 관련한 문제점이 발생한다.

훈련 세트의 크기 m이 아래와 같다고 할 때.

m = 100,000,000

\theta_j := \theta_j - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)} - y^{(i)})x_j^{(i)}

$\theta_j$ 하나를 계산할 때마다 매번 100,000,000 개의 값을 더하는 과정이 필요하며, 이 계산 비용은 꽤 크다.
이후의 강의에서 이 과정을 좀 더 효율적으로 바꿔줄 방법에 대해 배운다.
100,000,000개의 데이터를 전부 다 활용하지 않고 그 중 랜덤으로 1000개만을 뽑아서 사용하는 방법도 있다.
우선 1000개만으로 학습을 해본 뒤,
learning curve를 그려보고 전체 데이터셋을 사용하지 않아도 충분한 학습이 가능한지 확인한다.

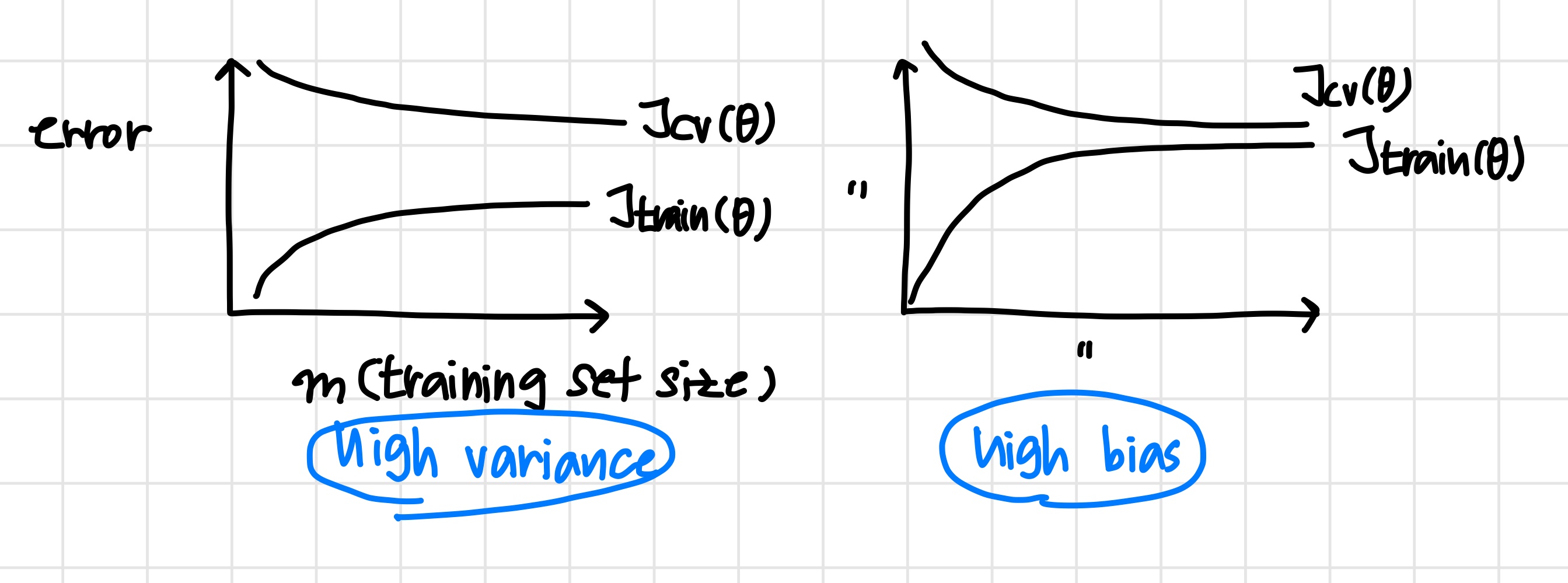
High bias 라면 데이터를 더 늘리는 것이 의미가 없다.

2) Stochastic Gradient Descent

데이터셋이 클 경우 경사하강법 연산 비용이 커지게 된다.

Linear regression with gradient descent

경사하강법을 사용해서 Linear regression을 훈련하고자 할 때 가설과 비용함수는 아래와 같으며, 비용함수의 그래프는 활 모양을 띈다.

h_\theta(x) = \sum_{j=0}^{n}\theta_jx_j

J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)} - y^{(i)})^2

경사하강법 수행은 다음과 같다.

\text{Repeat} \{ \theta_j := \theta_j - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \text{( for every j=0, ... , n) }\}

이때 m의 크기가 크다면 derivative term ( $\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}$ )의 연산비용이 커지게 된다.

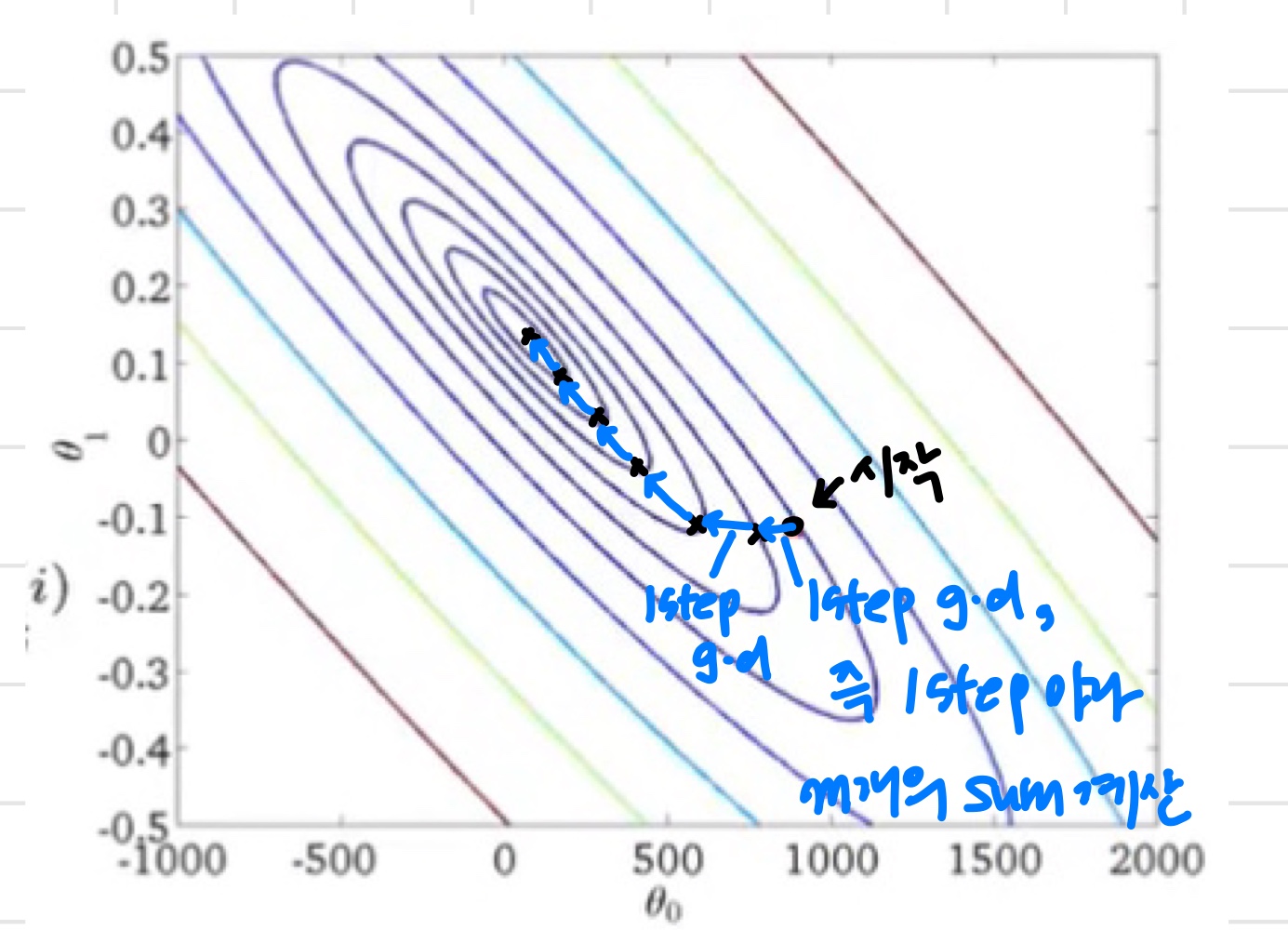
derivative term에서 m의 값을 전체 훈련 세트로 설정해두고 계산하는 것을 Batch gradient descent라고 한다.
매 iteration마다 훈련세트 전체를 고려하지 않는 것은 Stochastic gradient descent.

Stochastic gradient descent

Stochastic의 경우 Batch와 달리 전체 훈련세트를 훑고 $\theta_j$ 를 업데이트 하는 것이 아니기 때문에 최적값에 도달하는 과정에서 아래 그림과 같이 방향 전환이 많이 발생한다. 하지만 이때 속도는 더 빠르다.

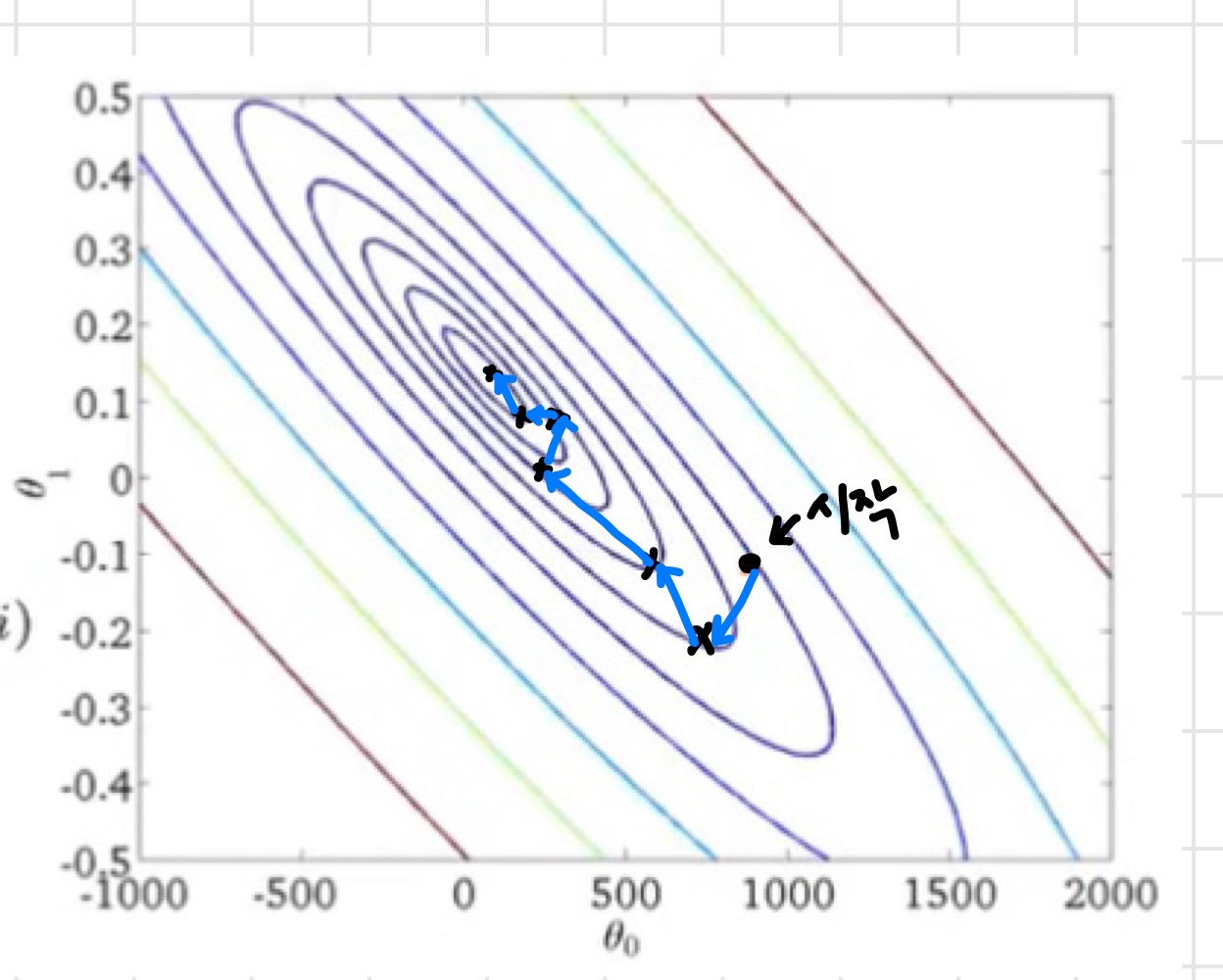
GD : 전체 데이터셋 , SGD : 샘플 1개

3) Mini-Batch Gradient Descent

Batch gradient descent : Use all $m$ examples in each iteration
Stochastic gradient descent : Use 1 example in each iteration
Mini-batch gradient descent : Use $b$ examples in each iteration
이때 $b$ 를 mini-batch size 라고 한다.

Mini-Batch Gradient Descent

mini-batch vs stochastic
mini-batch는 stochastic 보다 더 많은 샘플들을 살펴봐야 하지만 벡터를 이용한다면 오히려 더 빠른 연산이 가능하다.

4) Stochastic Gradient Descent Convergence

Checking for convergence

각각의 경사하강법들에서 convergence를 확인하는 방법.

Plot $cost(\theta, (x^{(i)}, y^{(i)})),$ averaged over the last 1000(say) examepls

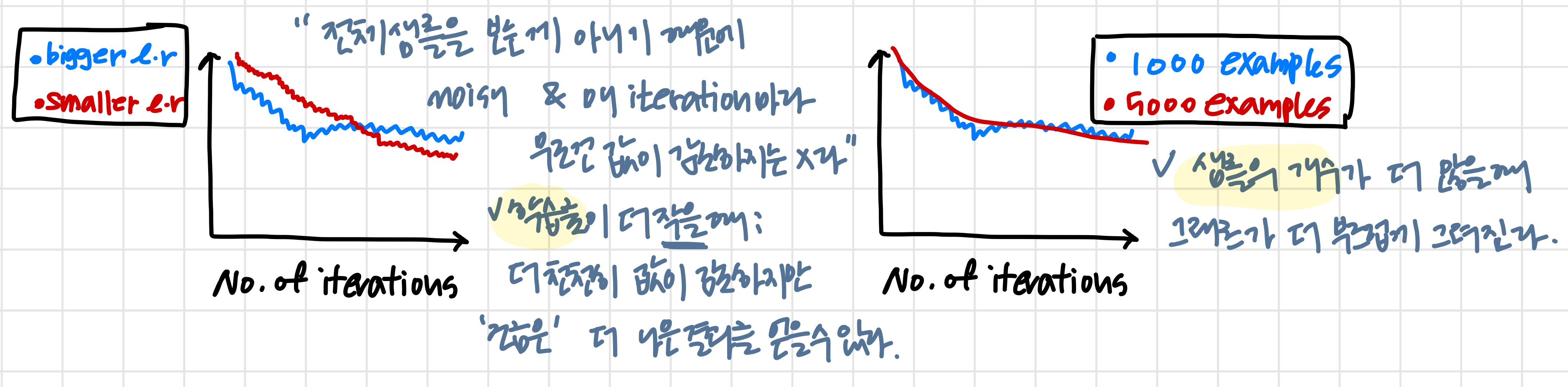
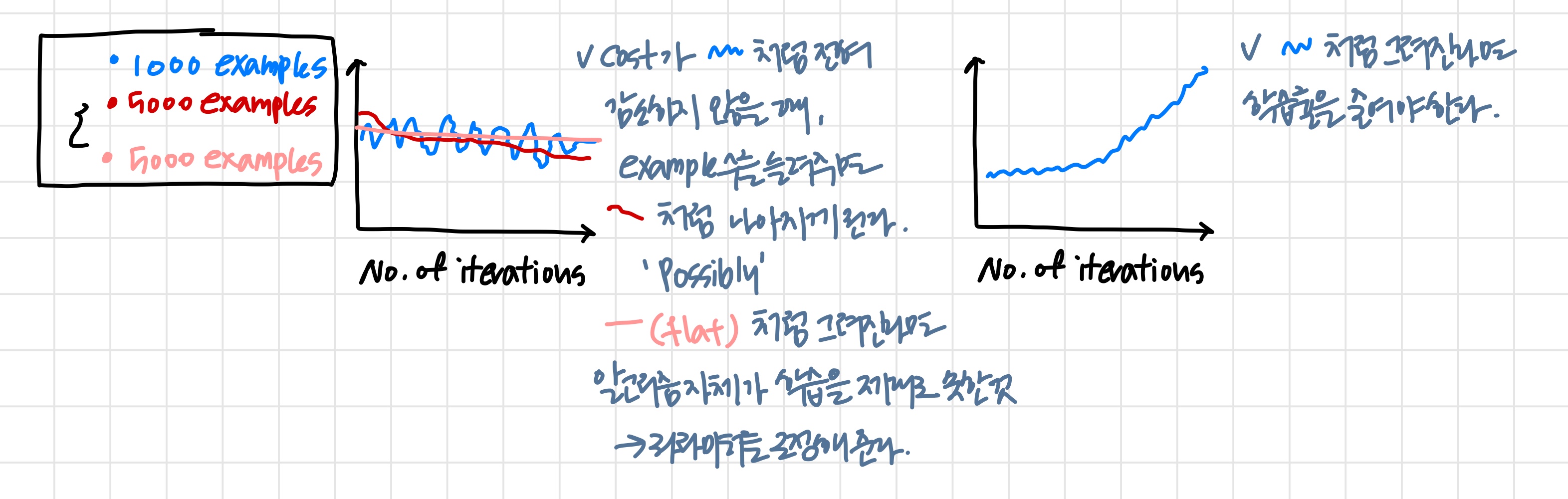
Stochastic gradient descent

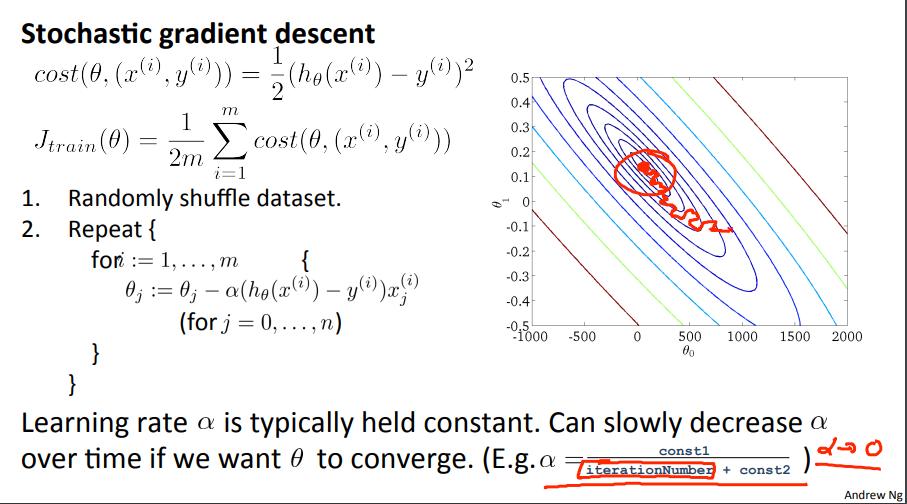
학습률의 값을 위와 같이 점점 감소시키면 같은 값을 유지한 것보다 더 좋은 결과를 얻을 수 있다.
If we reduce the learning rate α (and run stochastic gradient descent long enough), it’s possible that we may find a set of better parameters than with larger α.

비용 함수를 최적화하는 관점에서 stochastic gradient descent를 모니터링하는 방법에 대해 배웠다.
이 방법은 훈련 세트 전체가 아닌 일부만 이용한다.
이 방법으로 stochastic gradient descent가 제대로 동작하고 있는지, 즉 최적값으로 잘 수렴하고 있는지 확인할 수 있고 또한 학습률 α를 조정할 수 있다.