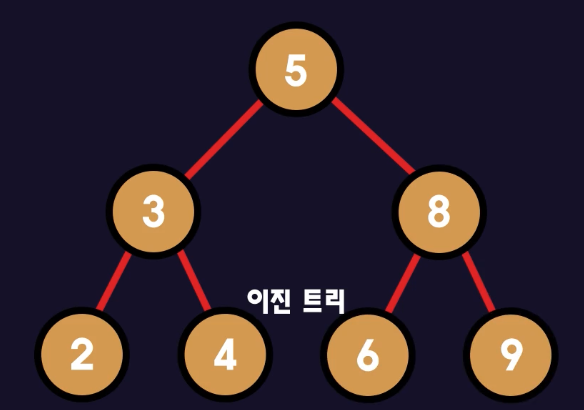
이진 탐색 트리

이진 탐색 트리

• 기본적으로 이진트리의 구조를 갖고있음.
• 데이터삽입, 제거, 검색이 빠름
• 중복된 노드가 없어야함
• 특정 노드의 왼쪽 자식노드는 그 노드의 값보다 항상 작은 값들로만 이루어짐
• 특정 노드의 오른쪽 자식노드는 그 노드의 값보다 항상 큰 값들로만 이루어짐
• 모든 자식 트리에도 위의 모든 규칙이 적용되어야 함

이진탐색트리의 기능

• 데이터 삽입
• 데이터 제거 (상대적으로 복잡함.)
• 데이터 탐색

이진탐색트리 추상자료형

이진탐색트리의 삽입

1. 루트노드값과 삽입할 노드의 값을 비교
2. 작다면 왼쪽 & 크다면 오른쪽으로 이동
3. 노드가 존재하지 않을 때까지 진행(null을 만날때까지)

구현코드

import { BinaryTree } from "./binaryTree.mjs";

class BinarySearchTree{
    constructor(rootNode = null){
        this.root=rootNode;
    }
    insert(data){
        // 이진탐색트리에 노드가 하나도 없을 떄
        if(this.root == null){
            this.root = new BinaryTree(data);
            return;
        }
        // 이진탐색트리에 노드가 이미 존재할 때
        let currentNode = this.root;
        let parentNode = null;

        while(currentNode != null){
            parentNode = currentNode;
            if (currentNode.getData() > data){
                currentNode = currentNode.getLeftSubTree();
            } else if (currentNode.getData() < data){
                currentNode = currentNode.getRightSubTree();
            }else{
                return;
            }
        }
        let newNode = new BinaryTree(data);
        if (parentNode.getData() > data){
            parentNode.setLeftSubTree(newNode);
        }else {
            parentNode.setRightSubTree(newNode);
        }
    }
    search(targetData){
        let currentNode = this.root;
        while(currentNode != null){
            if (currentNode.getData() == targetData){
                return currentNode;
            }else if (currentNode.getData() > targetData){
                currentNode = currentNode.getLeftSubTree();
            } else {
                currentNode=currentNode.getRightSubTree();
            }
        }
        // 데이터가 없는 경우
        return null;
    }
}

이진탐색트리의 제거

1. 터미널노드를 제거하는 경우