[자료구조] 트리 (Tree)

💁‍♀️ 트리 (Tree)

트리는 나무의 형태를 가진단방향 노드 기반 자료구조이다. 메모리 주소와 인덱스를 알면 데이터를 찾을 수 있는 배열 자료구조와 달리, 노드 기반 자료구조는 서로 인접하지 않은 메모리 셀 묶음으로 이뤄진다. 서로 인접하지 않은 각 데이터를 노드라고 한다. 트리 자료구조에는 아래와 같은 다양한 개념의 노드들이 있다.

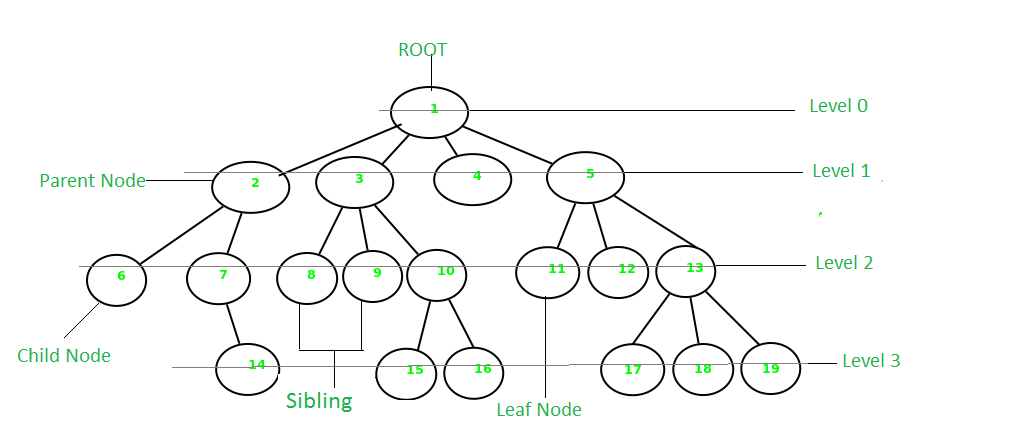
• 루트(Root): 트리의 꼭대기에 있는 가장 상위 노드.

• 부모 노드(Parent Node): 하위 계층으로 연결된 노드가 있는 상위 노드.

• 자식 노드(Child Node): 상위 계층에 연결된 노드가 있는 하위 노드.

• 리프 노드(Leaf Node): 자식 노드가 없는 노드.

위 그림을 보면 알 수 있듯이 트리 자료구조는 깊이에 대한 개념도 있다.

• 깊이 (Depth): 루트로부터 하위 계층의 특정 노드까지의 깊이. (위 이미지에서 노드2~5의 깊이는 1.)

• 레벨 (Level): 같은 깊이를 가지고 있는 노드를 묶어서 레벨로 표현. (루트의 레벨은 1, 노드2~5의 레벨은 2.)

• 높이 (Height): 리프 노드를 기준으로 루트까지의 높이. (노드7의 높이는 1.)
  

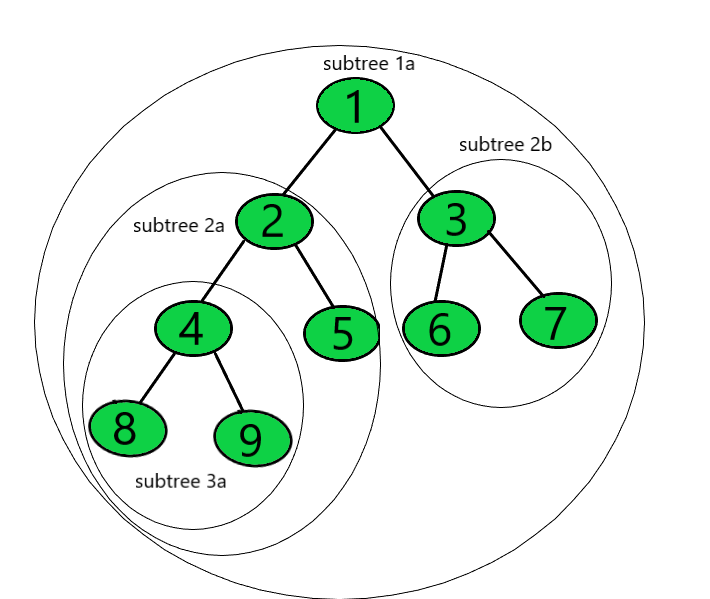
• 서브 트리(Sub tree): 큰 트리 내부에, 트리 구조를 갖춘 작은 트리.

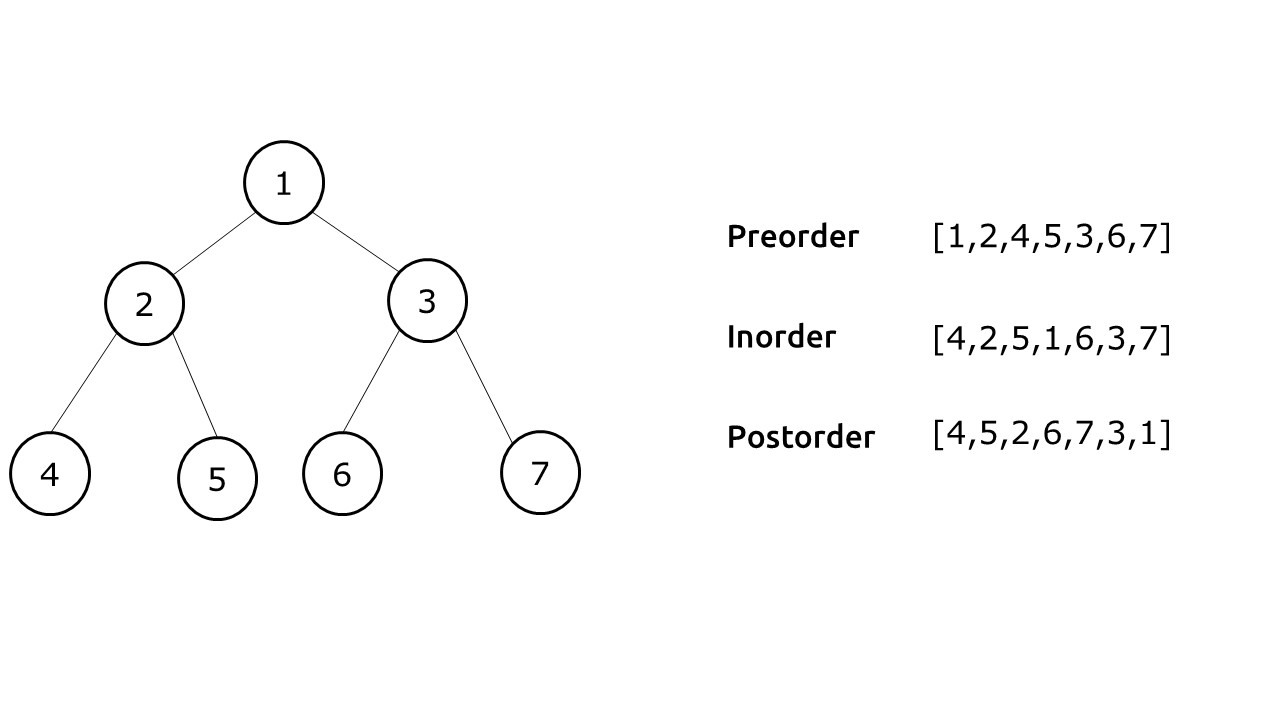
🌀 순회 방법

• 전위 (pre-order): 부모 노드를 먼저 방문하는 순회 방식. (순서: 부모->왼->오)

• 중위 (in-order): 왼쪽 노드를 방문하고 부모 노드를 방문하는 순회 방식. (순서: 왼->부모->오)

• 후위 (post-order): 하위/자식 노드를 방문하고 부모 노드를 방문하는 순회 방식. (순서: 왼->오->부모)

👉 메서드

트리와 노드 클래스의 대표적인 메서드는 다음과 같다.

메서드	설명
void addLeft()	현재 노드의 좌측에 노드 연결 정보 추가
void addRight()	현재 노드의 우측에 노드 연결 정보 추가
void deleteLeft()	현재 노드의 좌측에 노드 연결 정보 삭제
void deleteRight()	현재 노드의 우측에 노드 연결 정보 삭제
Node addNode(Object data)	현재 스택에 포함된 모든 데이터 삭제
void preOrder(Node node)	전위 순회 방법으로 출력
void inOrder(Node node)	중위 순회 방법으로 출력
void postOrder(Node node)	후위 순회 방법으로 출력

✨ 트리 구현

class Run {
    public static void main(String[] args) {
        // Tree 생성
        TreeExercise2 tree = new TreeExercise2();

        // 노드 생성
        TreeExercise2.Node node0 = tree.addNode(0);
        TreeExercise2.Node node1 = tree.addNode(1);
        TreeExercise2.Node node2 = tree.addNode(2);
        TreeExercise2.Node node3 = tree.addNode(3);
        TreeExercise2.Node node4 = tree.addNode(4);
        TreeExercise2.Node node5 = tree.addNode(5);
        TreeExercise2.Node node6 = tree.addNode(6);

        // 연결 관계 생성
        node0.addLeft(node1);
        node0.addRight(node2);
        node1.addLeft(node3);
        node1.addRight(node4);
        node2.addLeft(node5);
        node2.addRight(node6);

        // 트리 모양:
        //    0
        //  1   2
        // 3 4 5 6

        // 순회
        tree.preOrder(node1);
        System.out.println(); // 1 3 4
        tree.inOrder(node1);
        System.out.println(); // 3 1 4
        tree.postOrder(node1);
        System.out.println(); // 3 4 1

        // 노드 삭제
        node1.deleteLeft();
        node2.deleteRight();

        // 순회
        System.out.println(); // 1 4
        tree.preOrder(node1);
        System.out.println(); // 1 4
        tree.inOrder(node1);
        System.out.println(); // 4 1
        tree.postOrder(node1);
        System.out.println(); // (null)
    }
}
public class TreeExercise2 {
    int count;

    public TreeExercise2() {
        count = 0;
    }
    public class Node {
        Object data;
        Node left;
        Node right;

        public Node(Object data) {
            this.data = data;
            left = null;
            right = null;
        }
        public void addLeft(Node node) {
            left = node;
            count++;
        }
        public void addRight(Node node) {
            right = node;
            count++;
        }
        public void deleteLeft() {
            left = null;
            count--;
        }
        public void deleteRight() {
            right = null;
            count--;
        }
    }
    public Node addNode(Object data) {
        Node n = new Node(data);
        return n;
    }
    public void preOrder(Node node) {
        if (node == null) {
            return;
        }
        System.out.println(node.data + " ");
        preOrder(node.left);
        preOrder(node.right);
    }
    public void inOrder(Node node) {
        if(node == null) {
            return;
        }
        inOrder(node.left);
        System.out.println(node.data + " ");
        inOrder(node.right);
    }
    public void postOrder(Node node) {
        if(node == null) {
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.data+ " ");
    }

}

참고 자료
『 누구나 자료 구조와 알고리즘』