Shannon's Information Theory

Entropy

엔트로피는 정보량의 평균이다.

정보량은 낮은 확률의 사건이 일어날수록 유의미한 정보를 담고 있다는 가정이다.
단순한 1:1의 비율의 사건은 어떠한 일이 발생되는 놀랍지 않으나, 10000000:1의 비율로 특정 사건이 발생한 경우 이는 매우 큰 정보량을 가지게 된다.

단순히 정보량을 확률의 역수로 정의하면 해결될 것처럼 보이지만 그렇지 않다. 정보량의 평균을 위해선 단조 증가 함수로 인해 Log2를 사용하여 표시해야 한다.

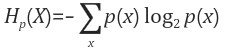
결국 Entropy는 정보량에 확률를 곱하고 더하여, 평균 값을 계산한 것이다.
어떠한 확률 분호 p(x)에서 일어날 수 있는 모든 사건들의 정보량에 평균, 즉 자체가 보유한 정보의 량을 뜻한다.

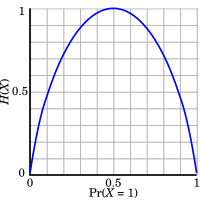
Shannon Entropy

Shannon이 제시한 Information Theory에서 Entropy는 확률 변수 기반의 Uncertainty에 대한 척도라 볼 수 있다. 이는 정보량에 대한 기댓값이며 Bit를 단위로 사용한다.

Discrete Data에 대한 Entropy를 Shannon Entropy라 시스템에서 유의미한 정보를 얻는데 필요한 기대 비용의 최소값이라 볼 수 있다.

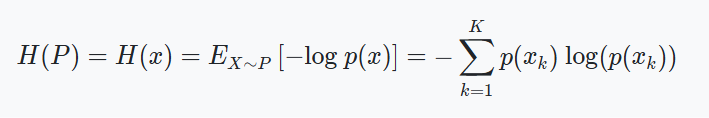
Entropy -> 이론적 확률 X 최적의 조건으로 실험 수행 비용 = 기대 비용의 최소값

Joint Entropy

확률 p(x)와 p(y)가 동시에 작용되어 일어날 확률은 p(x,y), 교집합을 통해 확장이 가능하다. Entropy도 동일하게 교집합을 통해 두 사건에 대한 교차된 Entropy를 구할 수 있다.

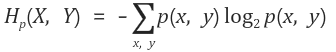
쉽게 보면 기존 Entropy에서 사건 2개에 대해서만 확장하였기에 p(x), P(y)가 된다.