해시 테이블
키와 값으로 구성된 검색 시스템
해시 테이블은 해시 함수를 사용해 검색을 수행한다. 보통 문자열인 키를 해시함수에 입력하면, 다음과 같이 배열의 인덱스에 매핑된 해시값이 생성된다.
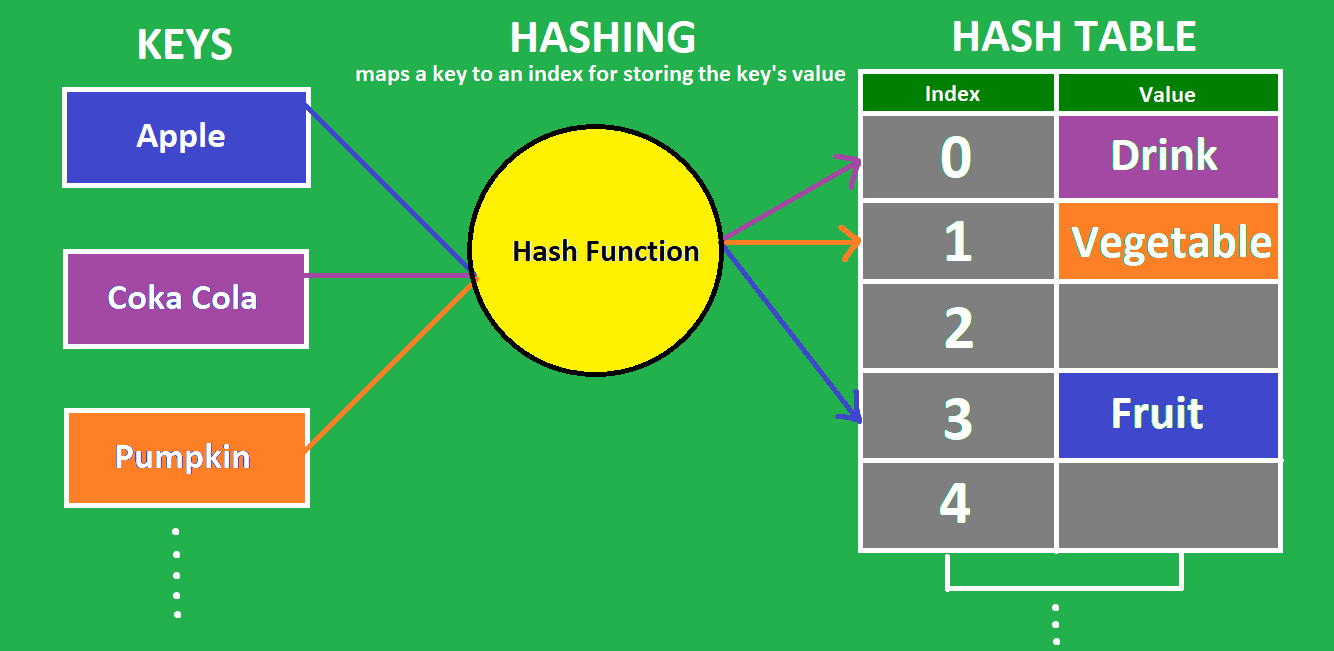
각 키와 값은 하나와 연결되어 있으므로 키를 알면 연결된 값을 즉시 찾을 수 있다. 따라서, 배열은 요소를 검색할때 O(N)의 시간복잡도를 갖는 것과 다르게 해시 테이블에서 요소를 검색할때 시간 복잡도가 O(1)이다.
해시충돌과 해결방법
해시 테이블은 효율적으로 검색할 수 있지만, 단점이 있다. 해싱에 사용되는 해시함수는 입력받은 키로 해시값을 생성하는데, 이때, 서로 다른 키를 입력했지만 같은 해시값을 리턴할 수 있다. 이것을 해시 충돌이라고 한다.
다음과 같은 방법으로 해시충돌을 해결할 수 있다.
Seperate Chaining (개별 체이닝)
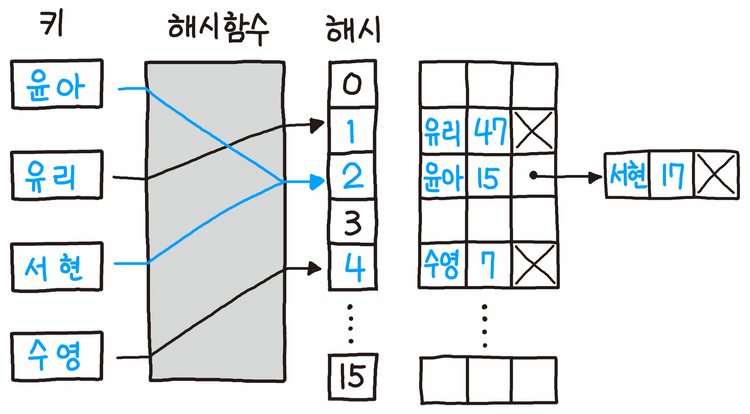
이미지 출처: 파이썬 알고리즘 인터뷰 p.286, 책만, 2020
체이닝은 배열의 요소에 연결리스트를 저장하는 방식이다. 테이블의 각 인덱스에 할당된 것은 값이 아니라 키와 값을 가진 연결리스트이다. 이 구조는 해시 충돌을 해결하는데 도움이 되지만, 연결리스트 형태로 키와 값을 저장하면 어떤 인덱스의 검색을 요청했을때 에러를 발생시키지 않고 연결리스트를 검색해서 원하는 데이터를 찾을 수 있다.
하지만, 체이닝을 사용하면 연결리스트가 길어졌을때, 해시 테이블의 검색 시간복잡도가 O(n)으로 증가할 수 있다.
Open Addressing
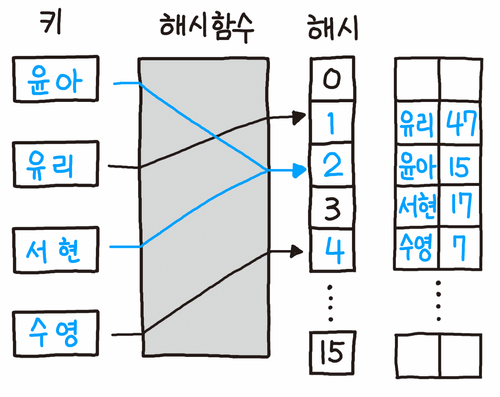
이미지 출처: 파이썬 알고리즘 인터뷰 p.287, 책만, 2020
오픈 어드레싱은 충돌이 발생했을때, 빈 공간을 탐사하는 방식이다. 이 방법에서 값은 모두 해시 테이블 자체에 저장되며 (체이닝 방식에서 키값이 연결리스트에 저장되는 것과는 다르다) 테이블의 크기는 키 개수보다 항상 커야한다.
가장 간단한 오픈 어드레싱 방법은 선형 탐사(linear probing)이며, 충돌이 발생할 경우 해당 위치부터 순차적으로 빈 공간을 탐사한다. 다른 방법으로는 제곱탐사 (quadaratic probing)가 있다.
예를 들어, 사이즈가 10인 해시테이블이 있고, 우리가 사용하는 hash함수는 키를 입력받아 인덱스값으로 3을 리턴한다고 가정해보자. 즉, [hash(x)%10] = 3 (여기서 10은 해시 테이블의 사이즈)인 함수인 경우이다. 그런데, 인덱스 3이 이미 찼다면, 선형탐사는 [3%10+1] = 4를 리턴해 4번째 인덱스에 값을 저장할 것이다.
제곱탐사는, [(3+1*1)%10] = 4를 리턴하고, 만약 4번째 인덱스도 차있다면, [(3+2*2)%10] = 7을 리턴해 7번째 인덱스에 값을 저장할 것이다.
충돌을 해결해도 결과적으로 충돌로 인한 성능 저하는 막을 수 없다. 수용률이 일정량을 넘어서면 저장과 조회 성능이 모두 떨어지며 아예 리스트 크리를 키운 뒤 재배열하는 방법을 사용한다. 이 과정은 비용이 많이 들고, 실시간으로 데이터를 처리하는 환경에는 적용하기 어렵다.
다른 방법으로는 Consistent hashing이라고 불리는 해시의 비트수를 늘이는 방법도 있다. 항목이 적을 때에는 적은 비트수의 해시와 작은 저장공간을 사용하다가 충돌이 잦아지면 비트수를 1비트 늘리고, 저장 공간도 2배로 늘린다.
해시에 대해 유튜브 영상을 찾아보던 중 consistent hashing을 사용한 load balancing에 대해 알게되었다. 아직 consistent hashing이 무엇인지 정확히 이해하지는 못했지만, 다음 주제로 이에 대해 정리해보면 좋을 것 같다.
reference