
ECDSA(Elliptic Curve Digital Signature Algorithm)의 타원 곡선 함수에 개인키 값을
대입하여 공개키를 얻는다.
K=k*G(k:개인키,G:상수)
이렇게 얻어진 공개키는 타원곡선 상의 한쌍의 좌표 x,y 이다.
이좌표의 x값과 y값을 이어 붙인 형식을 비압축형 공개키라고 한다
이경우에는 다른형식의 공개키와 구분하기 위해 값의 앞에 0x04를 추가한다.
그리고 압축형 공개키는 비압축형의 경우 520바이트의 저장공간이 필요하기때문에
공간을 줄이기 위해 압축한다 압축형 공개키는 x값으로만 공개키를 표현한다 . y
값은 생략하게 되고 다음 수식을 통해 도출할 수 있기 때문이다.
y^2=x^3+7
해당 함수 값에 대입하면 y값이 도출된다. y가 양수일 경우 K값 앞에 0x02를 음수일 경우
0x03을 추가하여 이를 구분한다.
이건 전에 내가 알아 보았던 타원곡선 함수다
Elliptic curve digital signature algorithm
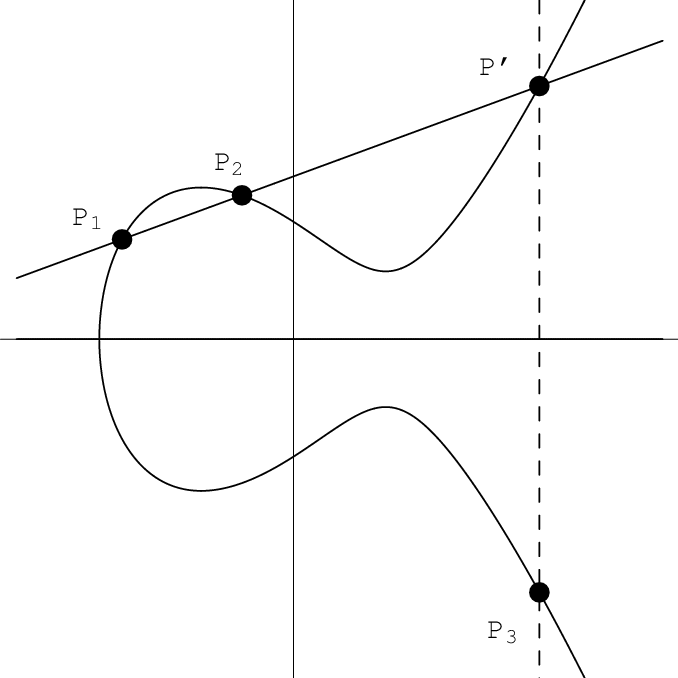
타원곡선의 성질
타원 곡선의 성질은 그래프가 생긴것이 타원은 아니지만
타원곡선 함수라 한다. 다음과 같이 정의 할수있다 .
타원곡선의 P1,P2,P3를 이은 직선을 다음과 같이 진행된다
P3 =P1 + P2 ( 여기서 p3는 음수를 양수화 한것 x축만 대칭해서 위치시켜준것)
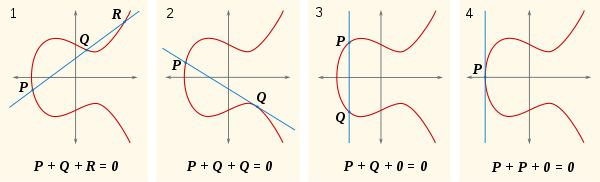
그리고 P1과 P2 여기선 P 와 Q,R로 나와있다 P와 Q 이은 직선이
이러한 모양을 보여줄 때도 있다 1번 그림과 같은 경우에는
직선을 이어 R을 만날수있지만 2,3,4번과 같은경우는 타원 곡선이 무한히
있는점에서 직선을 이었을때 만나지 못할수도 있다 이렇대는 0으로 값이 나온다.
공개키(Public key) (K=k(갠키)*G)
형식 1 비압축형
비압축형 좌표값 각각 256비트 x,y한쌍의 좌표이다 .
x와 y 거기에 비압축형은 04를 붙여 준다
-> K=04+x+y
형식 2 압축형
압축형 공개키는 x값만 공개키를 표현한다고한다 . y값은 생략하는데
y값은 다음과같이 나올수있다고 한다
그리고 y가 양수일경우 02 ,음수일 경우 03을 추가해 구분해준다
-> K = (02 or 03)+x
-> (y^2 = x^3+7) y값을 구하는 수식
개인키로부터 구한 공개키로 주소를 만든다
