[Java] 프로그래머스 - 사칙연산 (4단계)

📝 문제

프로그래머스 > 코딩테스트 연습 > 동적계획법(Dynamic Programming) > 사칙연산

---

📝 답안

📌 작성 코드

import java.util.*;
class Solution {
    int[][] min, max;
    public int solution(String arr[]) {
        int size = arr.length/2+1;
        min = new int[size][size];
        max = new int[size][size];
        
        int[] list = new int[size];
        
        for (int i = 0; i < arr.length; i+=2) {
            int num = Integer.parseInt(arr[i]);
            if (i == 0) {
                list[i/2] = num;
            } else {
                list[i/2] = arr[i-1].equals("+") ? num : -num;
            }
        }
        
        for (int i = size-1; i >= 0; i--) {
            for (int j = i; j < size; j++) {
                if (i == j) {
                    min[i][j] = list[i];
                    max[i][j] = list[i];
                } else {
                    min[i][j] = Integer.MAX_VALUE;
                    max[i][j] = Integer.MIN_VALUE;
                    
                    for (int k = i; k < j; k++) {
                        boolean value = k == i ? true : false; 
                        func(min[i][k], min[k+1][j], i, j, value);
                        func(min[i][k], max[k+1][j], i, j, value);
                        func(max[i][k], min[k+1][j], i, j, value);
                        func(max[i][k], max[k+1][j], i, j, value);
                    }
                }
            }
        }
        return max[0][size-1];
    }
    
    public void func(int a, int b, int x, int y, boolean value) {
        if (value && a < 0) {
            min[x][y] = Math.min(min[x][y], Math.min(a-b,a+b));
            max[x][y] = Math.max(max[x][y], Math.max(a-b,a+b));
        } else {
            min[x][y] = Math.min(min[x][y], a+b);
            max[x][y] = Math.max(max[x][y], a+b);
        }           
    }
}

---

✔ 정확성 테스트

테스트 1 〉 통과 (0.27ms, 74.8MB)
테스트 2 〉 통과 (0.21ms, 78.2MB)
테스트 3 〉 통과 (0.18ms, 73.2MB)
테스트 4 〉 통과 (0.28ms, 76.7MB)
테스트 5 〉 통과 (0.20ms, 72.4MB)
테스트 6 〉 통과 (0.23ms, 72.8MB)
테스트 7 〉 통과 (0.29ms, 78.3MB)
테스트 8 〉 통과 (0.20ms, 75.7MB)
테스트 9 〉 통과 (0.07ms, 74.6MB)
테스트 10 〉 통과 (0.04ms, 75MB)

✔ 효율성 테스트

테스트 1 〉 통과 (27.13ms, 54MB)
테스트 2 〉 통과 (29.36ms, 54.2MB)
테스트 3 〉 통과 (20.13ms, 54MB)
테스트 4 〉 통과 (36.63ms, 63.4MB)
테스트 5 〉 통과 (19.52ms, 53.1MB)
테스트 6 〉 통과 (23.50ms, 53.5MB)
테스트 7 〉 통과 (29.64ms, 54MB)
테스트 8 〉 통과 (26.98ms, 53.1MB)

---

📌 풀이 예시

테스트 케이스 ① 번으로 예시를 든다면

["1", "-", "3", "+", "5", "-", "8"]를 표로 표시한 것이 아래의 표이다.

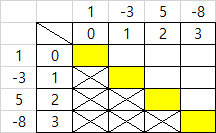
• 노란색으로 칠해진 곳은 해당 위치의 숫자를 넣으면 됨
• X자로 채워진 곳은 값 채울 필요 없음
• 그래서 내부 for문의 범위가 i부터 끝까지 감

for (int i = size-1; i >= 0; i--) {
     for (int j = i; j < size; j++) {

• 그리고 뒤에서부터 채우기 때문에 i는 점점 작아지는 식으로 구성

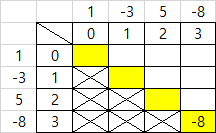
• i = 3 일 때 j = 3 일 때 [3][3] = -8
  => [3][3]의 최솟값, 최댓값은 -8

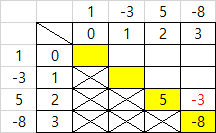
• i = 2 일 때 j = 2 일 때 [2][2] = 5 → 그리고 이 때를 기준으로 부호를 체크함
  => [2][2]의 최솟값, 최댓값은 5
• j = 3 일 때 [2][3] = [i][j-1] + [i+1][j] = 5 + -8 = -3
  => [2][3]의 최솟값, 최댓값은 -3

※ 기준 부호가 +일 경우에는 계산 시 부호의 변동이 발생하지 않아 최솟값과 최댓값은 동일하게 계산이 됨

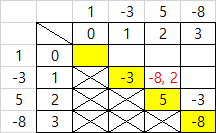
• i = 1 일 때 j = 1 일 때 [1][1] = -3 → 그리고 이 때를 기준으로 부호를 체크함
  => [1][1]의 최솟값, 최댓값은 -3
• j = 2 일 때 [1][2] = [i][j-1] + [i+1][j] = -3 + 5
  => 기준 부호가 -이므로 두 가지 방식으로 계산이 가능함 -(3+5) 또는 -3+5
  => [1][2]의 최솟값은 -8, 최댓값은 2

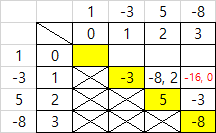
• j = 3 일 때 [1][3] = [i][j-2] + [i+1][j], [i][j-1] + [i+2][j]로 계산할 수 있음

[i][j-2] + [i+1][j]를 해석하면 [1][1]인 -3과 [2][3]인 (5 - 8)을 계산해서 나온 최솟값/최댓값을 이용하여 구하는 계산식임
=> 즉, -3 + (5-8) 이기 때문에 -3+(5-8)과 -(3+(5-8))로 계산식을 만들 수 있음
=> 두 계산식으로 구한 값 : -6, 0

[i][j-1] + [i+2][j]를 해석하면 [1][2]인 (-3+5)를 계산해서 나온 최솟값/최댓값과 [3][3]인 -8을 이용하여 구하는 계산식임
=> 즉, (-3+5)-8 이기 때문에 (-3+5)의 최솟값과 최댓값인 -8과 2를 이용하여 (-8)-8과 (2)-8의 계산식을 만들 수 있음
=> 두 계산식으로 구한 값 : -16, -6

• [1][3]의 최솟값 : -16, 최댓값 : 0

※ 기준 부호가 -이지만, 괄호를 활용하여 계산식을 구하는 문제이기 때문에 구분을 해줘야 함. 즉, -(3+5)-8과 -3+5-8로 계산을 해야하기 때문에 -8-8이라고 해서 -(8-8)의 계산식으로 만들면 안 됨.

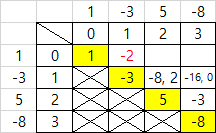
• i = 0 일 때 j = 0 일 때 [0][0] = 1 → 그리고 이 때를 기준으로 부호를 체크함
  => [0][0]의 최솟값, 최댓값은1
• j = 1 일 때 [0][1] = [i][j-1] + [i+1][j] = 1 -3
  => [0][1]의 최솟값, 최댓값은 -2

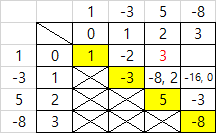
• j = 2 일 때 [0][2] = [i][j-2] + [i+1][j], [i][j-1] + [i+2][j]로 계산할 수 있음

[i][j-2] + [i+1][j]를 해석하면 [0][0]인 1과 [1][2]인 (-3+5)를 계산해서 나온 최솟값/최댓값을 이용하여 계산식을 만들어야 함
=> 즉, [1][2]의 최솟값은 -8, 최댓값은 2이므로 (1-8)과 (1+2)의 계산식을 만들 수 있음
=> 두 계산식으로 구한 값 : -7, 3

[i][j-1] + [i+2][j]를 해석하면 [0][1]인 (1-3)를 계산해서 나온 최솟값/최댓값과 [2][2]인 5을 이용하여 계산식을 만들어야 함
=> 즉, [0][1]의 최솟값/최댓값은 -2이므로 (-2)+5의 계산식을 만들 수 있음
=> 계산식으로 구한 값 : 3

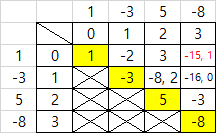
• j = 3 일 때 [0][3] = [i][j-3] + [i+1][j], [i][j-2] + [i+2][j], [i][j-1] + [i+3][j]로 계산할 수 있음

[i][j-3] + [i+1][j]를 해석하면 [0][0]인 1과 [1][3]인 (-3+5-8)을 계산해서 나온 최솟값/최댓값을 이용하여 계산식을 만들어야 함
=> 즉, [1][3]의 최솟값은 -16, 최댓값은 0이므로 (1) + (-16)과 (1) + (0)의 계산식을 만들 수 있음
=> 두 계산식으로 구한 값 : -15, 1

[i][j-2] + [i+2][j]를 해석하면 [0][1]인 (1-3)의 최솟값/최댓값과 [2][3]인 (5-8)를 계산해서 나온 최솟값/최댓값을 이용하여 계산식을 만들어야 함
=> 즉, [0][1]의 최솟값과 최댓값은 동일하게 -2, [2][2]의 최솟값과 최댓값 역시 동일하게 -3이므로 (-2) + (-3)의 계산식을 만들 수 있음
=> 계산식으로 구한 값 : -5

[i][j-1] + [i+3][j]를 해석하면 [0][2]인 (1-3+5)의 최솟값/최댓값과 [3][3]인 -8를 이용하여 계산식을 만들어야 함
=> 즉, [0][2]의 최솟값과 최댓값은 동일하게 3, [3][3]은 -8이므로 (3) + (-8)의 계산식을 만들 수 있음
=> 계산식으로 구한 값 : -5

• [0][3]의 최솟값 : -15, 최댓값 : 1

---

📌 후기

정확도 테스트의 케이스 1번만 계속 실패라고 떠서 진짜 2시간은 끙끙 앓았는데 결국 풀어낸 내 자신.. 칭찬해..☆★