아니 프로그래머스 Lv.2 .. 정녕 이것들이 Lv.2가 맞습니까..?!
고렙존에서 초보자용 몽둥이 들고 있는 느낌이 들지만
어찌저찌 때려 맞힌 문제 중 하나 공유합니다
문제는 여기에서 확인하시면 됩니다
정답만 보고싶으시면 아래로 가주세요
핵심 로직
const foo = (n) => {
return foo(n-1)*4 - foo(n-2)
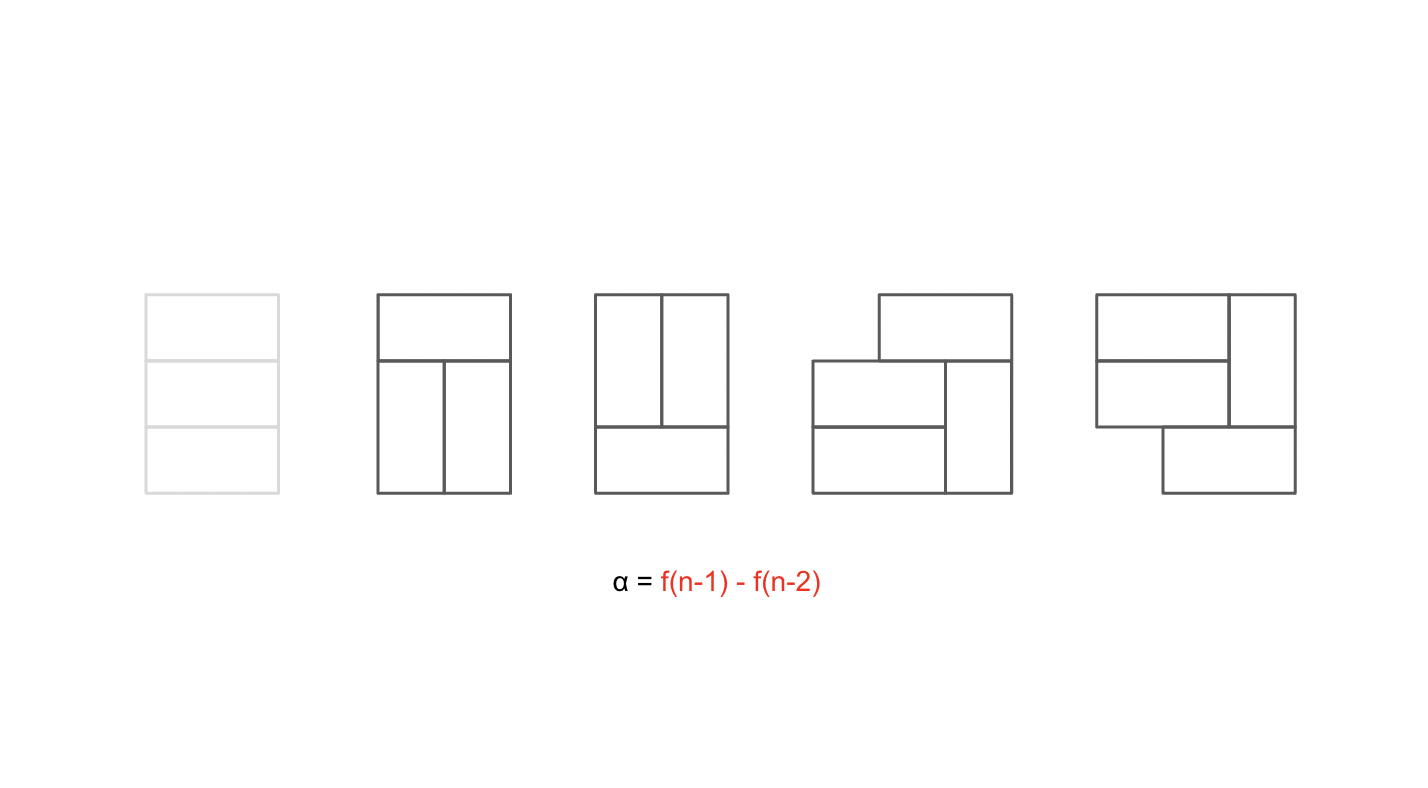
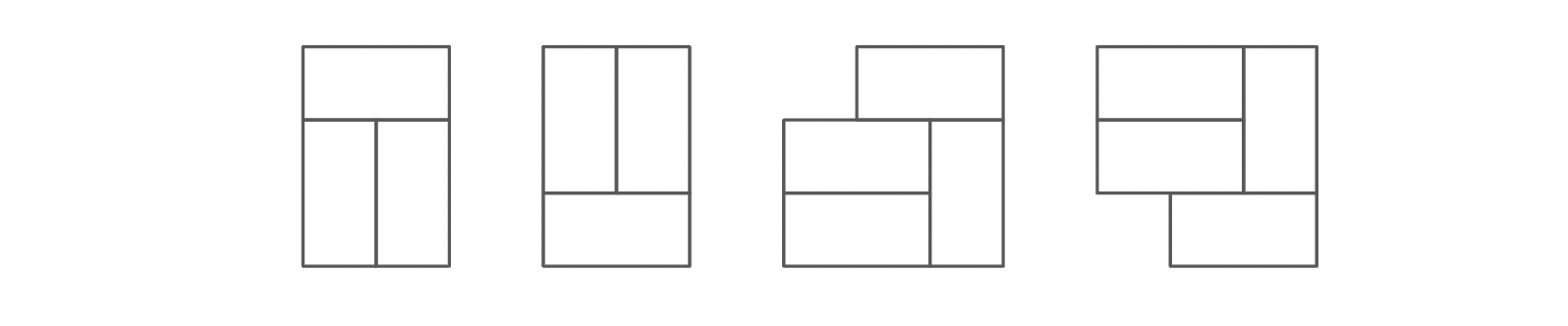
}3X2의 타일은 다음 세 가지의 경우의 수를 갖습니다
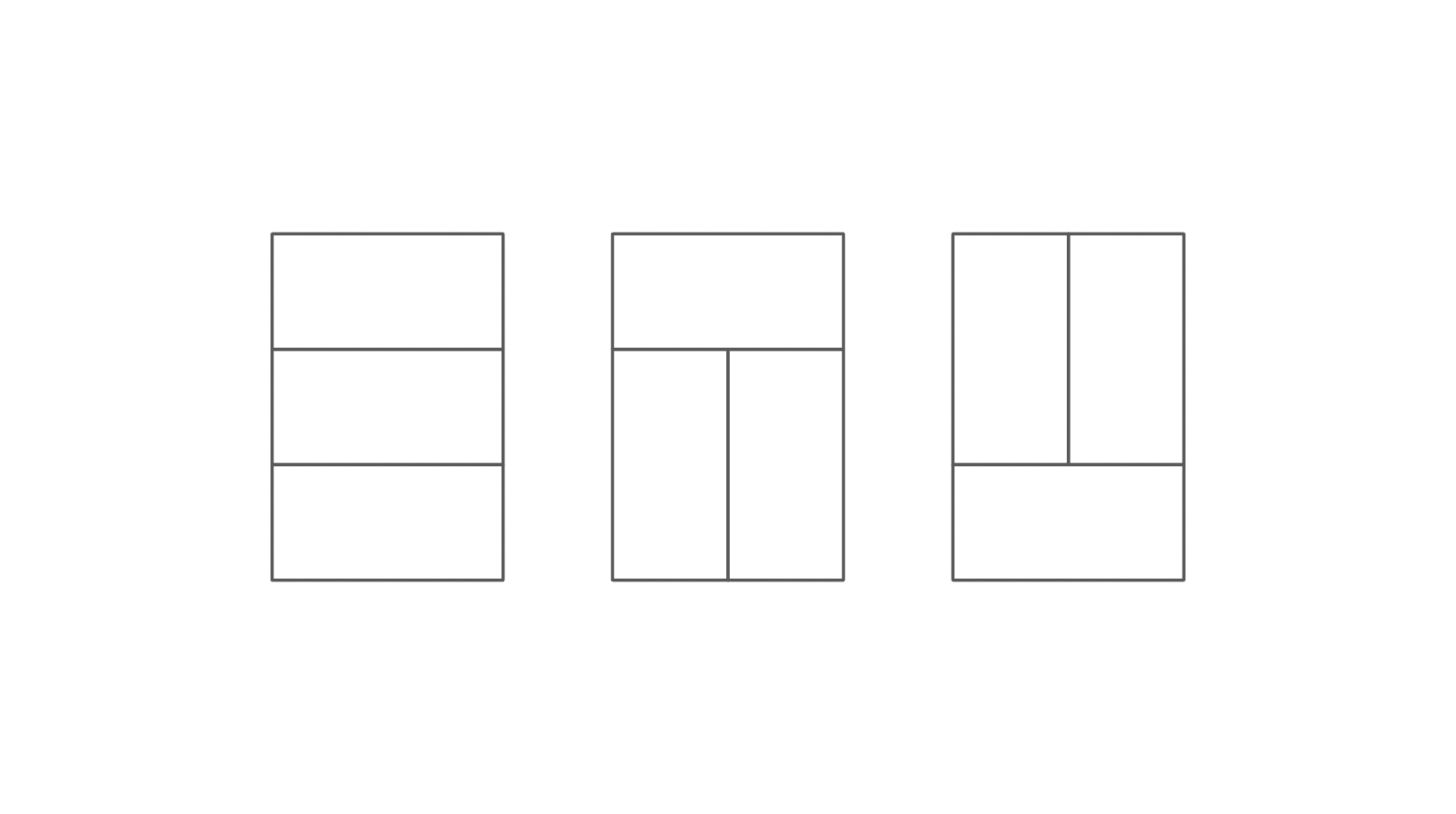
그렇다면 타일이 추가될 때 경우의 수가 3배가 된다고 생각했습니다
하지만 더 추가될 수 있는 경우의 수가 있습니다
이 경우를 특수 케이스라고 지칭하고 +α로 표기했습니다
+α 는 마지막 타일들이 다음과 같이 배치될 경우를 위해 존재합니다
마지막 타일들은 위와 같이 두 가지 모양으로 고정되지만,
앞 타일들의 경우의 수를 계산해야 합니다
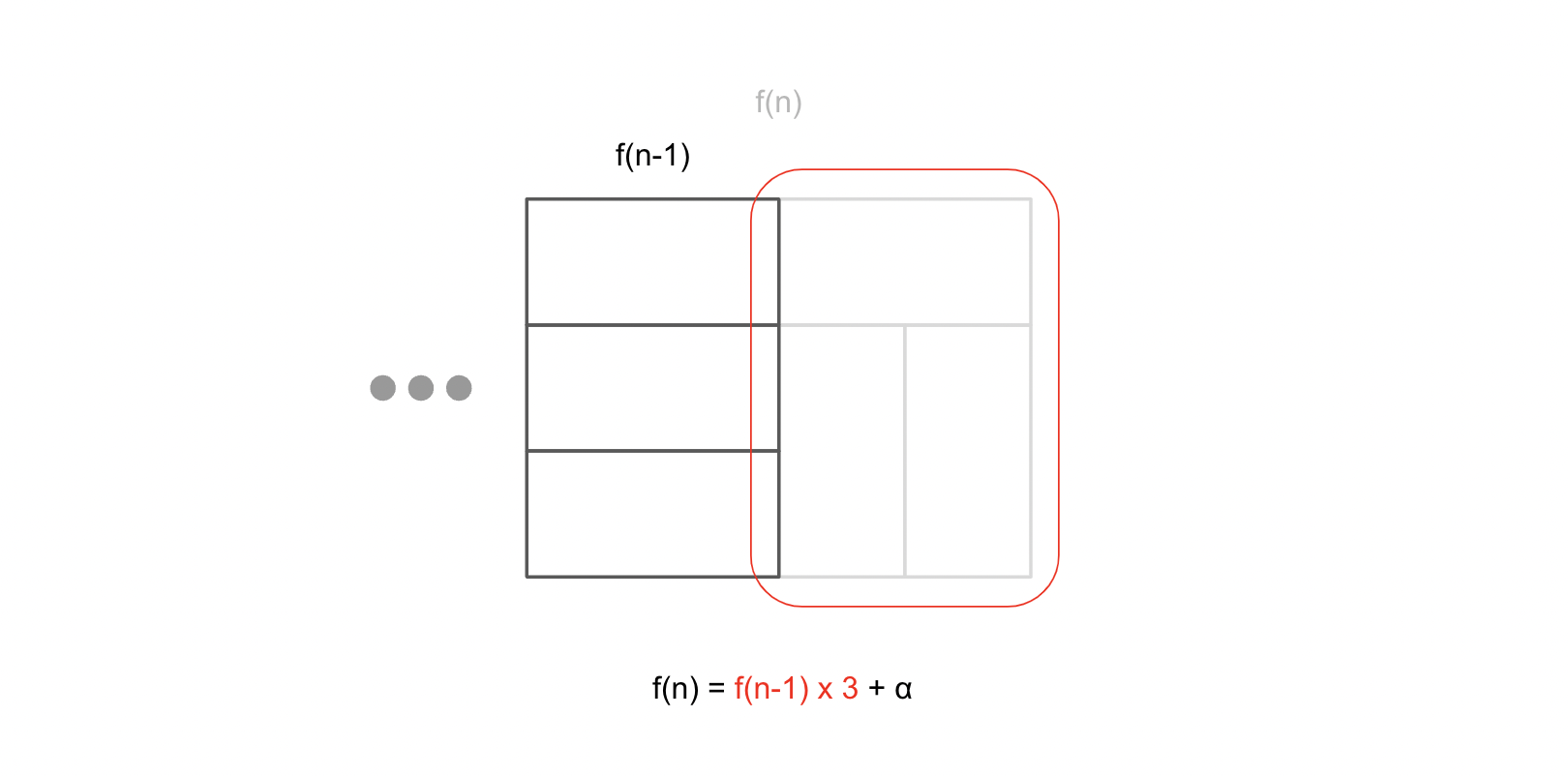
마지막 타일들을 지우고 생각해 보려고 노력했고
아래와 같이 붉은색 타일이 고정된 경우와 같다고 생각하게 됐습니다
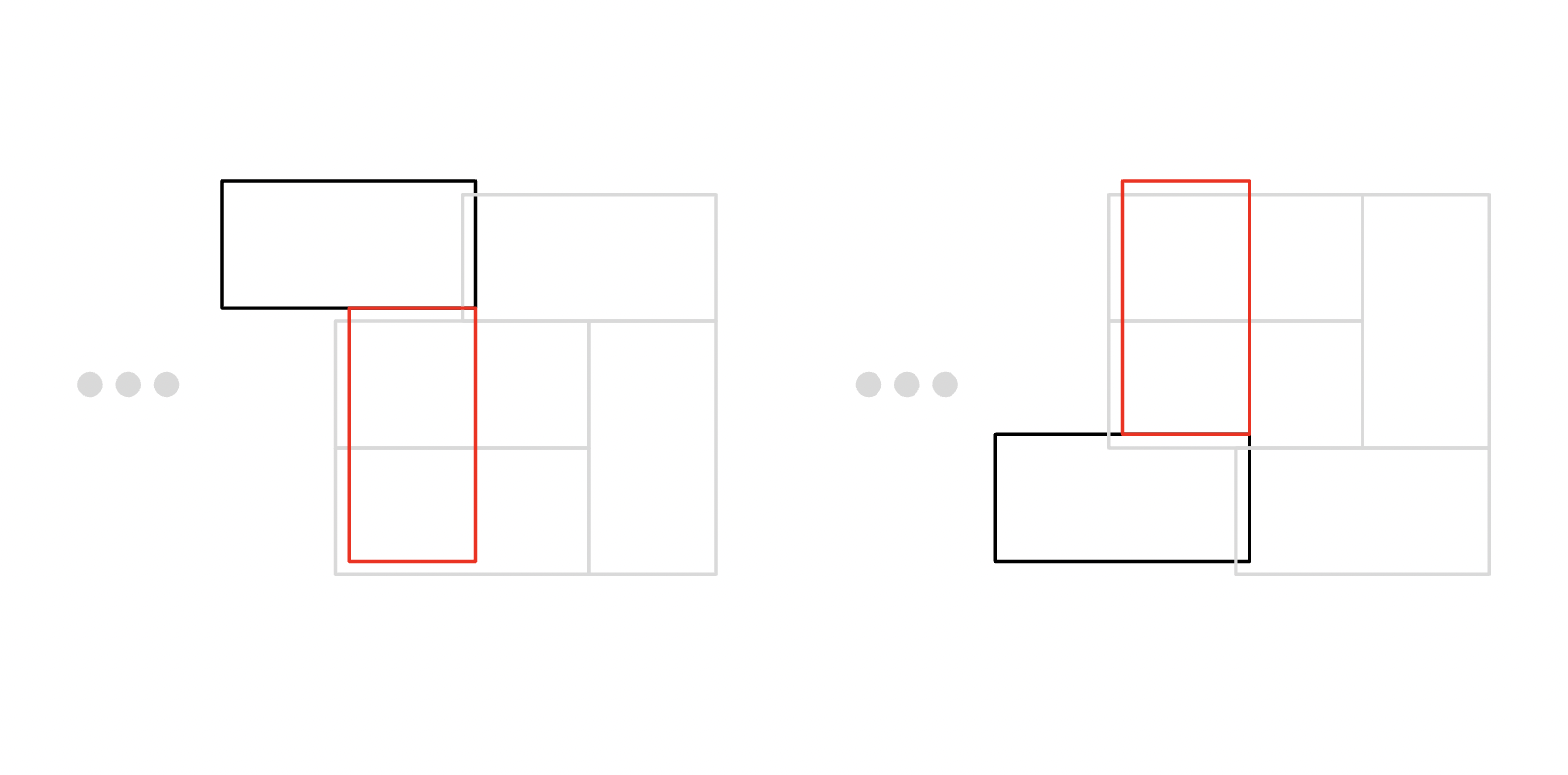
하지만 이 때의 경우의 수를 세자니 n - 1 의 타일들도 특수 케이스를 갖고 있을 것이고
규칙성을 찾기 어려울 것 같았습니다
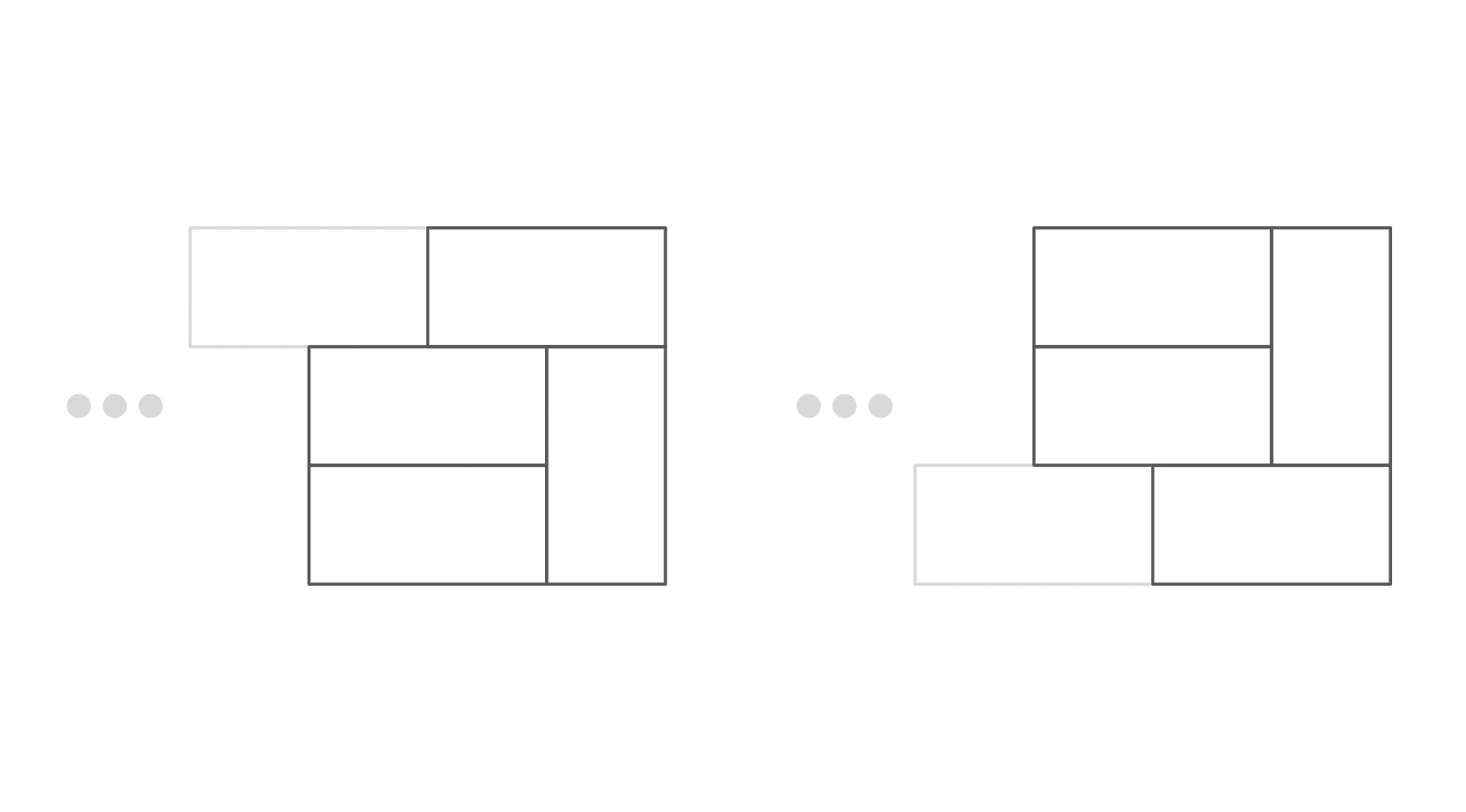
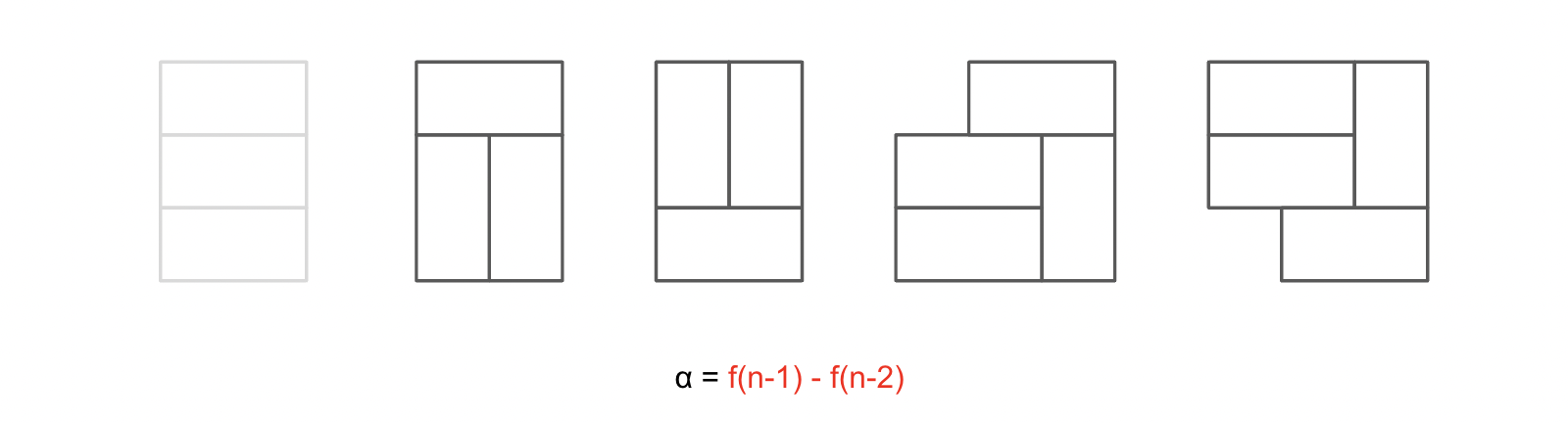
다음 네 가지 경우의 합을 세기 어렵다면
남은 유일한 경우의 수를 제외하는 것은 어떨까요
이 경우의 수는 아주 쉽게 특정지을 수 있습니다
바로 n - 2 의 타일들의 경우의 수와 같죠

그래서 +α 는 이렇게 됩니다
결국 아래와 같은 식이 도출되고,
f(n) = f(n-1)*3 + (f(n-1) - f(n-2))
축약하면 이렇게 됩니다
f(n) = f(n-1)*4 - f(n-2)
함수로 표현하면 다음과 같이 표현할 수 있겠죠
const foo = (n) => {
return foo(n-1)*4 - foo(n-2)
}제출 과정
풀이 과정이 맞는지 확인하기 위해 일단 제출합니다 ( 두근두근 )
function solution(n) {
let mod = 1_000_000_007;
return foo(n/2) % mod;
}
const foo = (n) => {
if(n === 1) {
return 3;
}else if(n === 2){
return 11;
}else {
return foo(n-1) * 4 - foo(n-2);
}
}이런 젠장, 타임아웃이 반기네요
아마도 재귀함수 탓인것 같습니다
수정합니다
function solution(n) {
let mod = 1_000_000_007;
let arr = [1, 3];
for(let i = 1 ; i < n/2; i ++){
arr = [arr[1], arr[1] * 4 - arr[0]];
}
return arr[1] % mod;
}타임아웃은 벗어났지만 이번에도 통과하지 못합니다
혹시 숫자가 너무 큰가 싶어서 solution(1000) 을 찍어보니
NaN 이 찍히네요
다음과 같이 수정하고, 통과했습니다
function solution(n) {
let mod = 1_000_000_007n;
let arr = [1n, 3n];
for(let i = 1 ; i < n/2; i ++){
arr = [arr[1], arr[1] * 4n - arr[0]];
}
return arr[1] % mod;
}통과한 답
function solution(n) {
let mod = 1_000_000_007n;
let arr = [1n, 3n];
for(let i = 1 ; i < n/2; i ++){
arr = [arr[1], arr[1] * 4n - arr[0]];
}
return arr[1] % mod;
}p.s.
사실 이런 문제 풀이를 공유할 생각은 없었는데
이 문제를 잠깐 구글링 해 보니 입맛에 맞는 설명이 없었습니다
'다른 설명보다 내 풀이 과정이 더 이해가 잘 될 분들이 있지 않을까' 라는 생각이 들어
이렇게 공유하게 됐네요
