[프로그래머스 - Lv2] 2 x n 타일링 (JS)

3 x n 타일링 올렸으니 요놈도 한번 올려봅니다

핵심 로직

const foo = (n) => {
  return foo(n-1) + foo(n-2);
}

과정

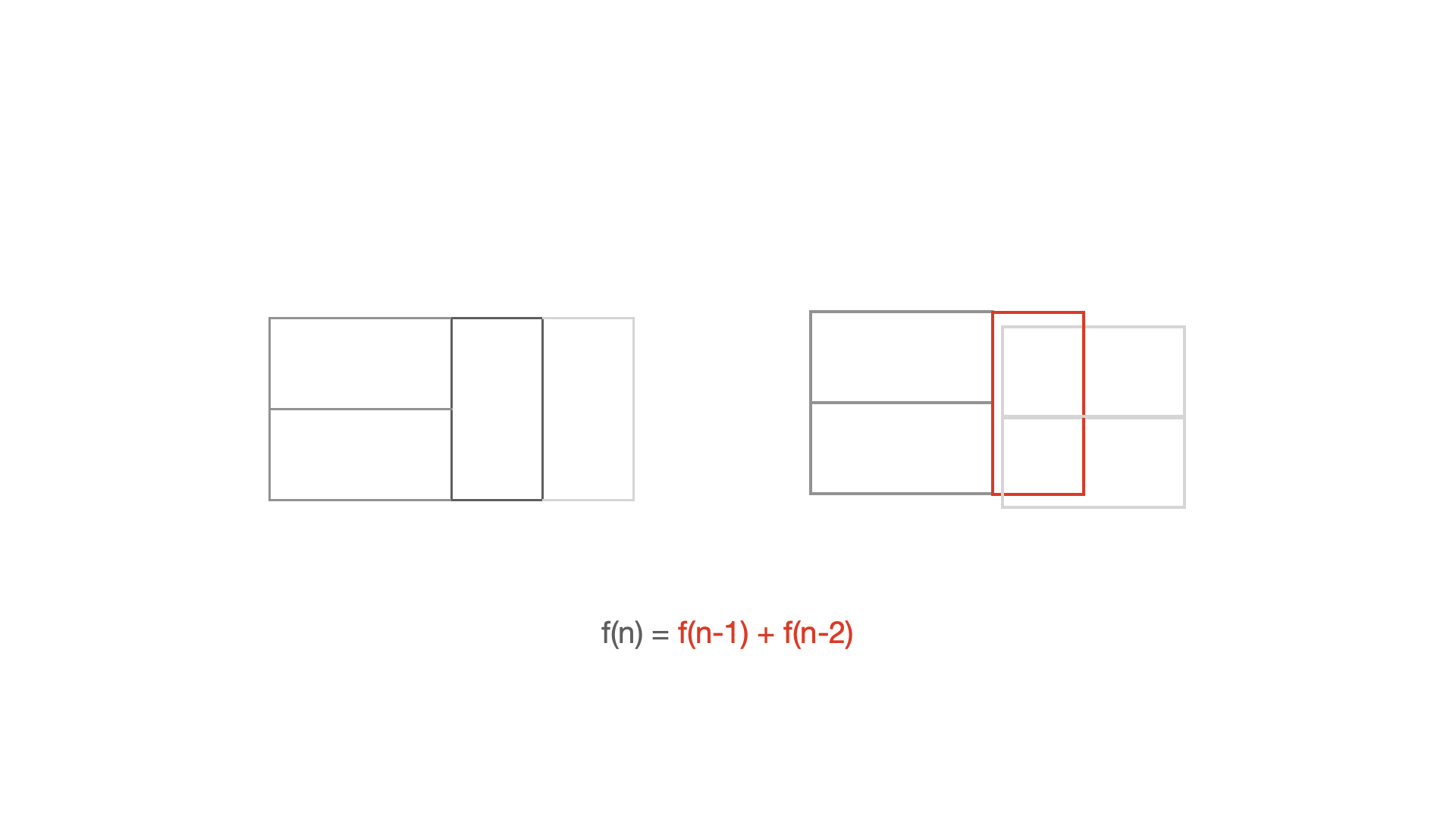
3 x n 타일링과 같은 순서로 생각해 봅니다

타일이 추가될 때 다음과 같이 경우의 수가 증가합니다

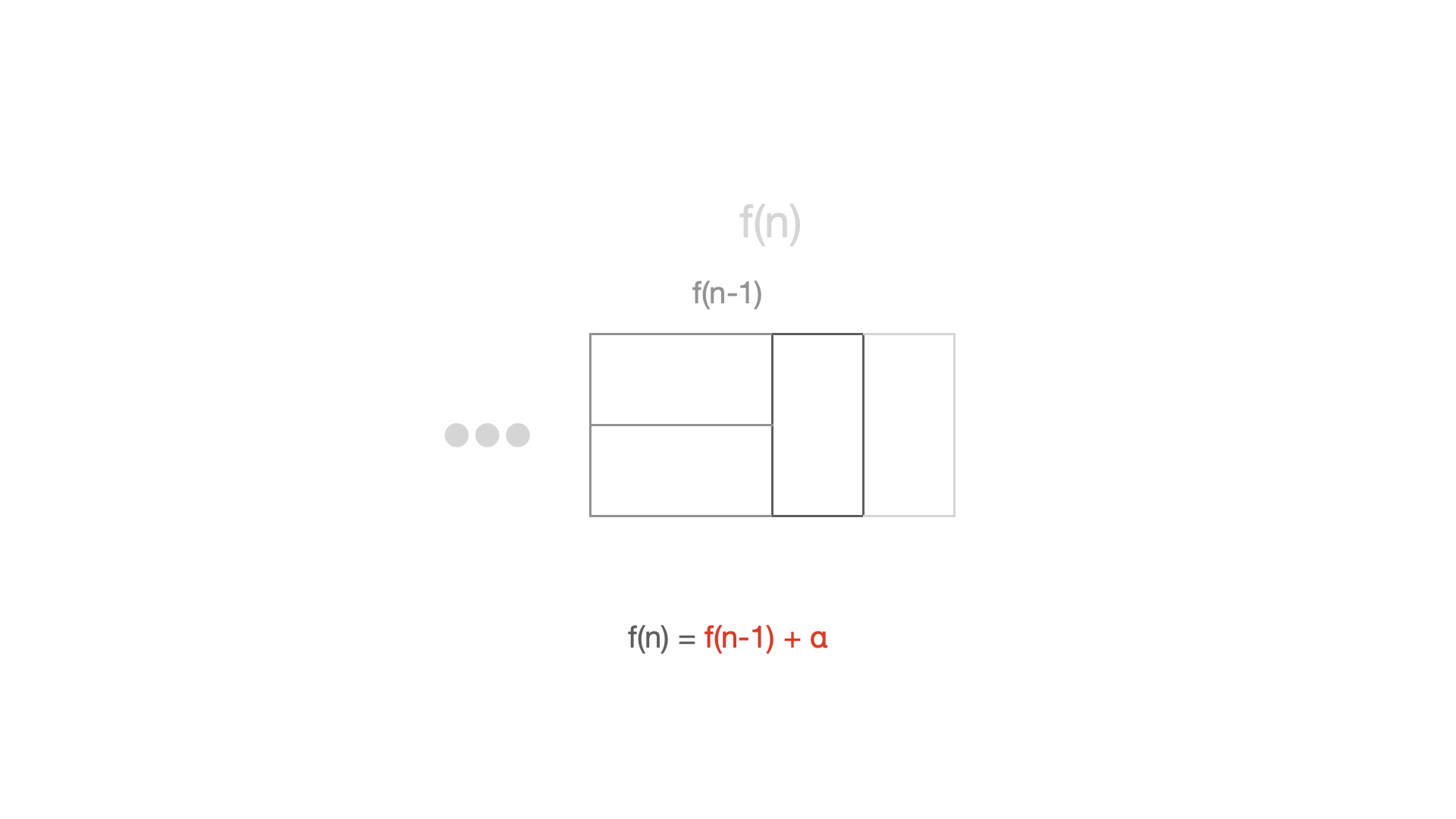
2 x n 타일링에서의 +α 는 쉽습니다

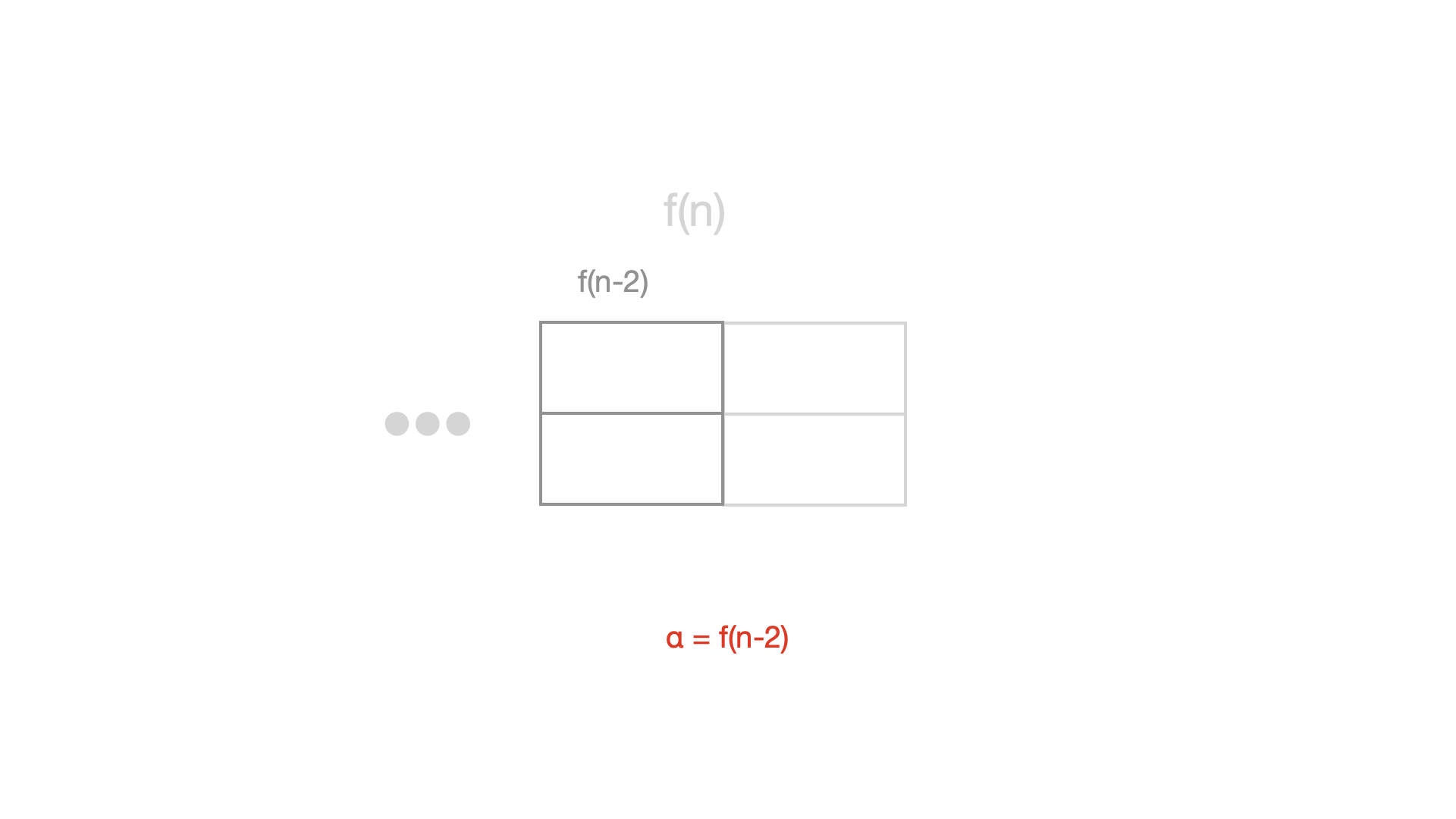
이걸 합치면 다음과 같은 식이 도출됩니다

f(n) = f(n-1) + f(n-2)

어디서 많이 보던 식이죠?

네 피보나치 수열입니다

통과한 답

function solution(n) {
    let mod = 1_000_000_007n;
    let [prev, curr] = [1n, 1n];
    
    for(let i = 1; i < n ; i++){
        [prev, curr] = [curr, (prev + curr) % mod];
    }
    
    return curr;
}