유니캐스트 라우팅

유니캐스트 라우팅에서 패킷은 포워딩 테이블을 참조하여 발신지에서 목적지까지 홉단위로 전달된다.

이때 발신지 호스트는 자신의 패킷을 로컬 네트워크의 기본 라우터에 전다랗면 되기 때문에 발신지 호스트는 포워딩 테이블이 필요 없다.
목적지 호스트 역시 로컬 네트워크에서 목적지 호스트의 기본 라우터로부터 패킷을 전송받으면 되기 때문에 포워딩 테이블이 필요하지 않다.

이것은 인터넷에서 네트워크에 있는 라우터만 포워딩 테이블이 필요하다는 것을 의미한다.

최소 비용 라우팅

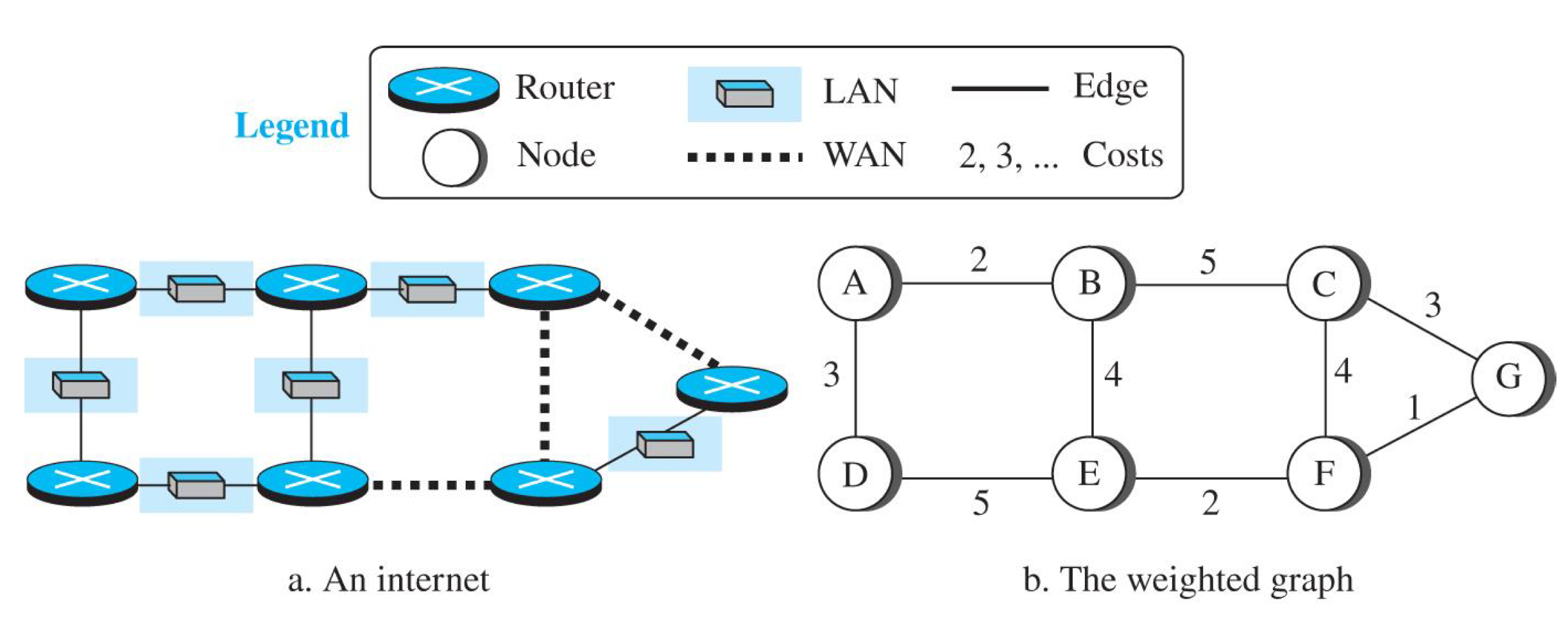
최소 비용 라우팅이란 가중치 그래프로 인터넷을 모델링할 때, 근원지 라우터부터 목적지 라우터까지의 최적 경로를 표현하는 방법 중 하나이다.

두 라우터 사이의 최소 비용(least cost)를 찾는 것이다.

위의 그림에서 A와 E의 최선의 경로는 A-B-E라는 것을 알 수 있다. 각 라우터는 최소 비용 경로를 찾아 라우팅해야한다.

최소 비용 트리

인터넷에 N개의 라우터가 있는 경우 각 라우터에서 다른 라우터까지의 최소 비용 경로는 N-1개 이다.

이는 전체 인터넷에 대해 N*(N-1) 개의 최소 비용 경로가 필요하다는 것을 의미한다.

최소 비용 트리는 이러한 모든 경로를 확인하는 방법이다.

최소 비용트리는 소스 라우터를 루트로 하여 전체 그래프에 걸쳐있고 루트와 다른 노드 사이의 경로가 가장 짧은 트리이다.

거리-벡터 라우팅

1. 각 노드의 인접한 노드들의 정보를 이용하여 최소 비용 트리를 구한다.
2. 불완전한 트리는 계속 완전한 트리가 되기위해 수정한다.
3. 각 라우터들은 자신이 가지고 있는 인터넷 정보가 불완전해도 정보들을 주위 라우터들에게 끊임없이 알려준다.

벨만-포드 방정식

$D_xy = min{(c_xa+D_ay), (c_xb+D_by), (c_xc+D_cy), ...}$

벨만-포드 방정식은 거리-벡터 라우팅의 핵심으로 거리 벡터 라우팅의 내부적으로 완전한 트리를 만들기 위해 사용되는 알고리즘이다.

이 방정식은 소스 노드와 목적지 노드 사이의 비용이 일부 중간 노드를 통해 소스 노드와 목적지 노드의 최소 비용을 찾는데 사용된다.

거리-벡터

최소 비용 트리는 트리의 루트에서부터 모든 목적지까지의 최소 비용 경로 정보를 가지고 있다.
이 정보들을 일차원 배열로 표현한 것을 거리 벡터라고 한다.

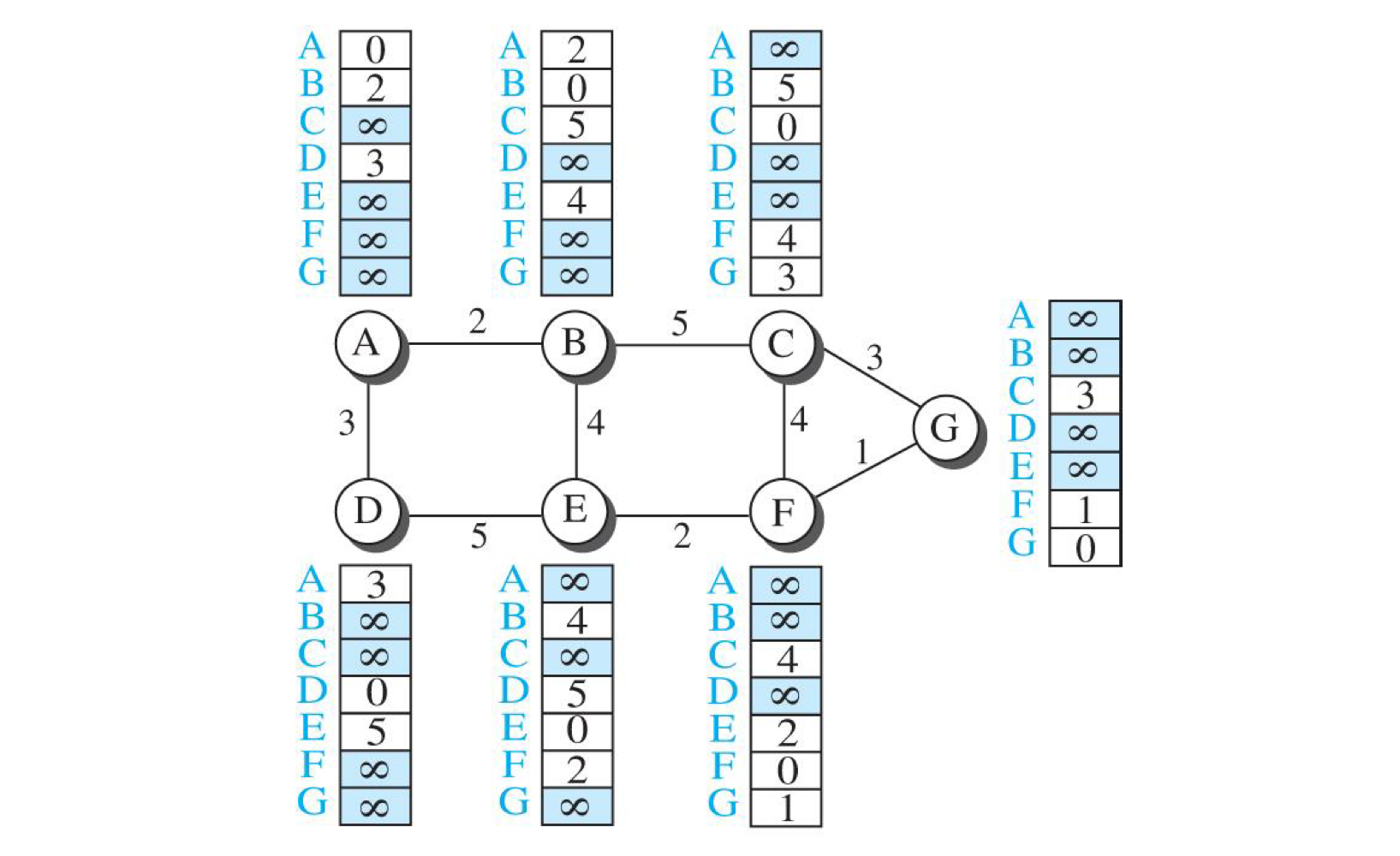
각 라우터는 주변 노드와의 비용정보를 활용하여 거리 벡터를 생성한다.
이때 초기값을 모르는 경우에는 무한대로 표시한다.

거리-벡터 갱신

불완전한 트리를 완전한 트리로 바꾸기 위해서 거리-벡터를 계속 최저 비용으로 갱신해야한다.

거리-벡터 갱신 과정

1. 모든 노드가 벡터를 만든 후 인접한 노드와 벡터 정보를 교환한다.
2. 이웃으로부터 벡터 정보를 수신한 노드는 벨만-포드 방정식을 이용하여 자신의 거리 벡터를 갱신한다. (최저 비용정보를 갱신)
3. 백터가 갱신되면 자신의 모든 이웃에게 전달한다.
4. 전역적인 최소 비용을 찾을 수 있다.

거리-벡터 라우팅의 불안정성

링크-상태 라우팅

링크 상태 정보를 모든 라우터에게 전달해 최단 경로 트리를 구성하는 라우팅 프로토콜 알고리즘입니다.
Network에 대한 전반적인 정보(Topology, path)를 가지고 라우터와 라우터 간 가능성 있는 모든 경로 정보를 교환합니다.
거리와 대역폭에 따라 경로를 계산하고 어떤 링크의 변화가 있는 경우만 정보를 전달하는 방식을 취합니다.
다익스트라(Dijkstra) 알고리즘을 사용합니다.
네트워크를 일관성 있게 파악할 수 있으나 거리 벡터 알고리즘에 비해 계산이 복잡하고 트래픽을 광범위한 범위까지 전달합니다.
대규모 네트워크에 적합합니다.
해당되는 대표적인 라우팅 프로토콜은 OSPF 입니다.

OSPF(Open Shortest Path First)

규모가 크고 복잡한 TCP/IP 네트워크에서 RIP의 단점을 개선하기 위해 자신을 기준으로 링크 상태 알고리즘을 적용해 최단 경로를 찾는 라우팅 프로토콜

다익스트라 알고리즘 사용
최단 경로 탐색에 다익스트라 알고리즘을 사용하는 내부 라우팅 프로토콜
링크 상태 라우팅 기반 메트릭 정보를 한 지역 내 모든 라우터에 변경이 가능했을 때만 보내 라우팅 테이블을 구성, 계산
네트워크 변화에 신속하게 대처
최소 지연, 최대 처리량 등 관리자가 라우팅 메트릭 지정
AS 분할 사용
자치 시스템을 지역으로 나눠 라우팅을 효과적으로 관리
홉 카운트에 제한이 없음
멀티캐스트를 사용해 정보를 전달

경로-벡터 라우팅

거리-벡터 라우팅과 링크 상태 라우팅은 최소비용을 이루는 것을 목적으로 한다.
이와 반대로 경로-벡터 알고리즘은 최소비용을 이루는것이 최우선이 아닌 경우에 사용하는 라우팅 알고리즘이다.

예를 들어 인터넷에 발신자가 자신의 패킷이 통과하는 것을 금지하고 싶은 어떤 라우터들이 있다고 가정할 때 발신자는 라우터에게 특정한 규칙을 적용시킬 수 있다.
이때 최소 비용 라우팅 알고리즘을 사용하는 경로-벡터 라우팅과 링크 상태 라우팅은 최소 비용 경로상에 이러한 라우터가 있을 때 패킷이 이 라우터를 통과하지 못하도록 하는 것이 불가능하다.

이런 경우에는 발신자가 라우터에게 특정한 규칙을 적용시킬 수 있는 경로-벡터 라우팅을 이용해야한다.

스패닝 트리

경로-벡터 라우팅은 스패닝 트리를 이용해 최적의 경로를 결정한다.
이때 스패닝 트리는 최소 비용 트리가 아닌 스패닝 트리 고유 규칙을 적용해 발신지로부터 작성되는 트리이다.
벨만-포드 방정식과 비슷하지만 최소 비용이 아닌 고유 규칙을 이용한다.

$Path(x, y) = best {Path(x, y), [(x + Path(v, y)]}$

경로-벡터 갱신

1. 부팅시 만들어 지는 경로 벡터
   

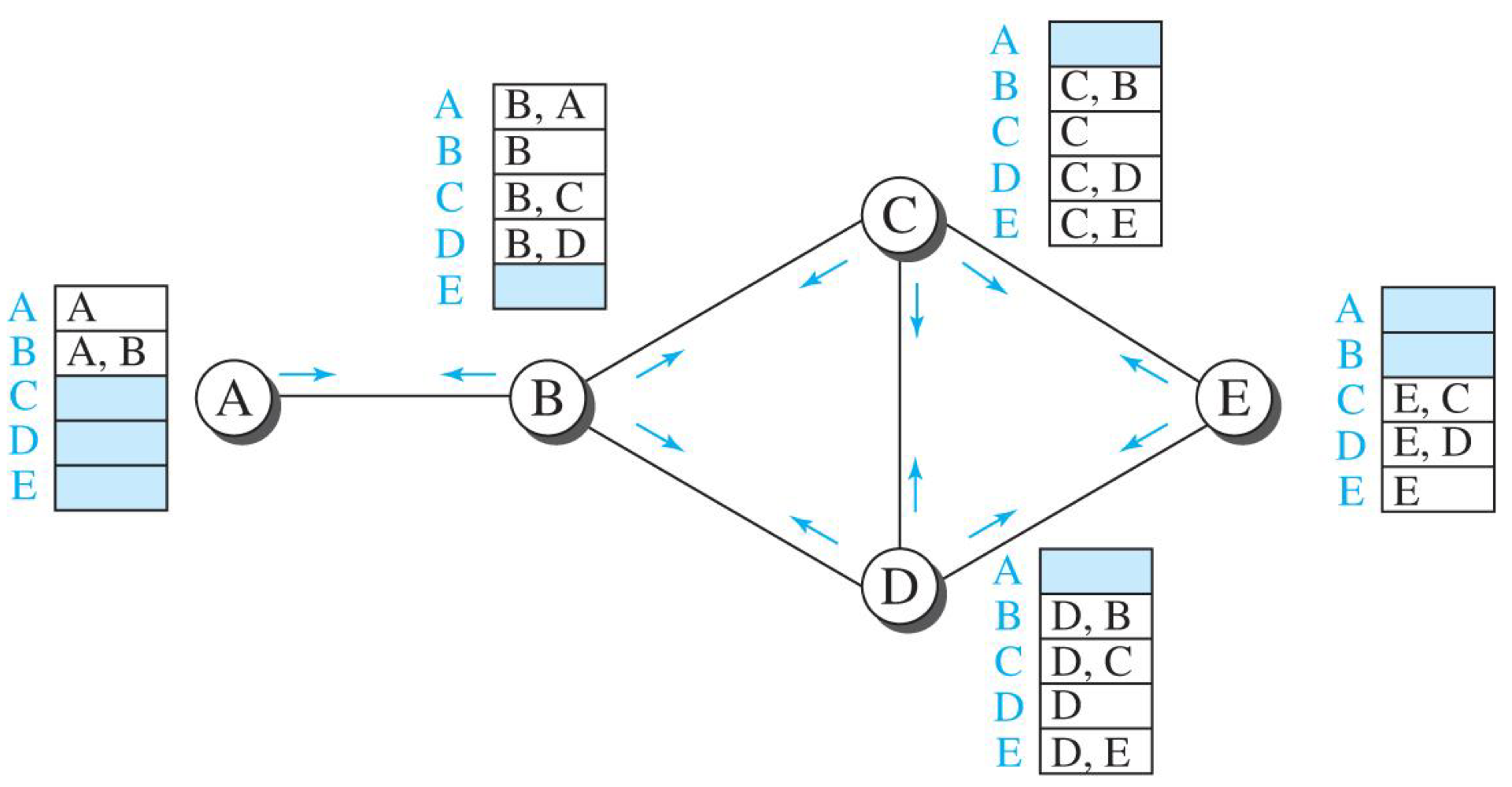
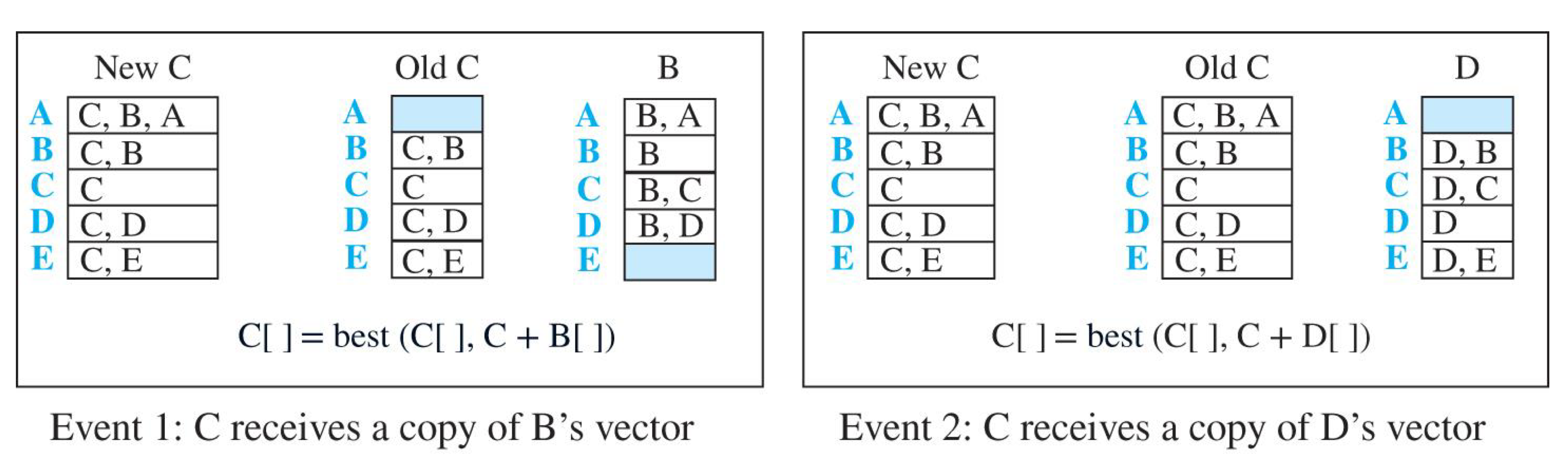
2. 경로-벡터 갱신
   인접한 노드로부터 경로-벡터 정보를 받아 갱신한다.