[알고리즘] 동적계획법 (Dynamic Programming, DP)

동적 계획법

동적계획법 이란, 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 모든 작은 문제들을 한 번만 풀어야 한다. 따라서 정답을 구한 작은 문제의 답은 어딘가에 메모해놓는다. 다시 그 보다 큰 문제를 풀어나갈 때, 똑같은 작은 문제가 나타나면 앞서 메모한 작은 문제에 대한 결과값을 이용하는 것이 DP 이다.

즉, 상향식 접근법으로, 가장 작은 부분의 해답을 구한 뒤 이를 저장하고, 저장한 값을 이용하여 상위 문제를 풀어가는 방식이라고 하면 되겠다. 이때 동적계획의 핵심은 Memoization(메모이제이션) 이라는 기법이다.

사실 일반적인 재귀(Naive Recursion) 방식은 DP와 매우 유사하다. 하지만 가장 큰 차이점은 일반적인 재귀를 단순히 사용 시 동일한 작은 문제들이 여러 번 반복 되어 비효율적인 계산될 수 있다는 것이다.

예를 들어 피보나치 수를 재귀로 구현한다면 다음과

동적계획법의 조건

동적 계획법을 적용하기 위해서는 위 정의에서 본 것처럼, 두 가지 조건을 만족시켜야 한다.

• 부분 반복 문제 (Overlapping Subproblem)
• 최적 부분 구조 (Optimal Substructure)

부분 반복 문제 (Overlapping Subproblem)

동적계획법의 등장은 피보나치 수열이라고 한다. 피보나치 수열은 대표적인 재귀함수로, 아래와 같이 표현할 수 있다.

func fibo(_ n: Int) -> {
	if n <= 1 { return n }
    fibo(n - 1) + fibo (n - 2)
}

만약 fibo(7) 을 구하는 과정을 도식화 해보면, 아래 이진 트리와 같다.

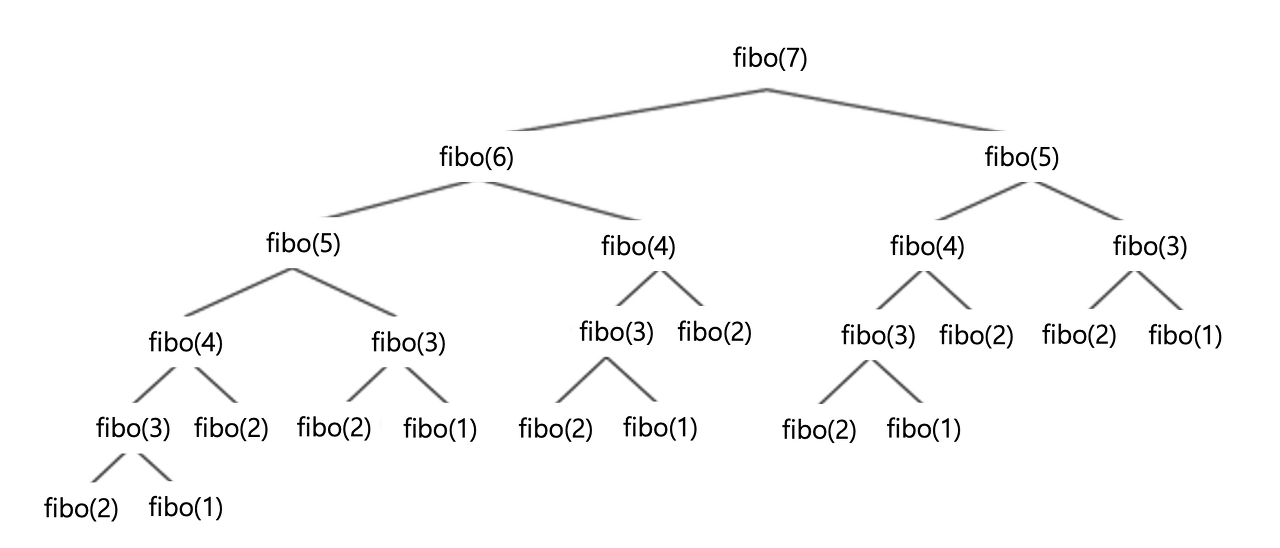
7번째 값을 구하기 위해서는 총 25번의 함수가 호출된다는 것을 알 수 있다. 이 과정에서 fibo(5), fibo(4), fibo(3)들이 이미 진행했던 연산임에도 불구하고 재귀되며 반복적으로 연산하는 것을 볼 수 있다.

이러한 반복적인 연산을 부분 반복 문제 (Overlapping Subproblem) 이라고 한다. 이는 어떤 문제가 여러 개의 부분 문제로 쪼개질 수 있을 때 사용하는 용어이다.

이때 부분문제 (subproblem) 란 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀 알고리즘을 통해 해결되는 문제를 가르킨다.

최적 부분 구조 (Optimal Substructure)

최적 부분 구조란, 작은 부분 문제에서 구한 최적의 답으로 합쳐진 큰 문제의 최적의 답을 구할 수 있어야 한다는 것이다.

만약, A - B까지의 가장 짧은 경로를 찾고자 하는 경우를 예시로 할 때, 중간에 X가 있을 때, A - X / X - B가 많은 경로 중 가장 짧은 경로라면 전체 최적 경로도 A - X - B가 정답이 된다.

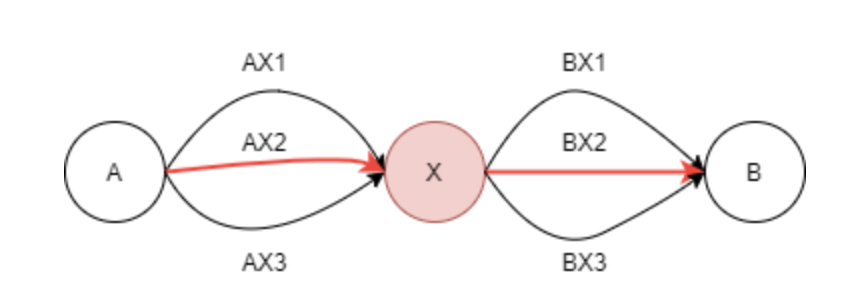
위의 그림에서 A - X 사이의 최단 거리는 AX2이고 X - B는 BX2이다. 전체 최단 경로는 AX2 - BX2이다. 다른 경로를 택한다고 해서 전체 최단 경로가 변할 수는 없다.

이와 같이, 부분 문제에서 구한 최적 결과가 전체 문제에서도 동일하게 적용되어 결과가 변하지 않을 때 DP를 사용할 수 있게 된다.

DP 구현 방법

DP는 2가지 방식으로 구현할 수 있다.

• Bottom-Up (Tabulation 방식) - 반복문 사용
• Top-Down (Memoization 방식) - 재귀 사용

Bottom-Up

Bottom-Up은 아래에서 부터 계산을 수행 하고 누적시켜서 전체 큰 문제를 해결하는 방식이다.

메모를 위해서 dp라는 배열을 만들었고 이것이 1차원이라 가정했을 때, dp[0]이 기저 상태이고 dp[n]을 목표 상태라고 한다면 Bottom-up은 dp[0]부터 시작하여 반복문을 통해 점화식으로 결과를 내서 dp[n]까지 그 값을 전이시켜 재활용하는 방식이다.

var cache = [Int](repeating: 0, count : 101)

cache[1] = 1
cache[2] = 1

func fibo(_ n: Int) -> Int {
	for i in 3...n {
    	cache[i] = cache[i-1] + cache[i-2]
    }
    
    return cache[n]
}

Top-Down

Top-Down은 dp[0]의 기저 상태에서 출발하는 대신 dp[n]의 값을 찾기 위해 위에서 부터 바로 호출을 시작하여 dp[0]의 상태까지 내려간 다음 해당 결과 값을 재귀를 통해 전이시켜 재활용하는 방식이다.

피보나치의 예시처럼, f(n) = f(n-2) + f(n-1)의 과정에서 함수 호출 트리의 과정에서 보이듯, n=5일 때, f(3), f(2)의 동일한 계산이 반복적으로 나오게 된다.

이 때, 이미 이전에 계산을 완료한 경우에는 단순히 메모리에 저장되어 있던 내역을 꺼내서 활용하면 된다. 그래서 가장 최근의 상태 값을 메모해 두었다고 하여 Memoization 이라고 부른다.

//범위보다 1크게
// cache[0] 초기값 상태 0으로 모두 채워줌
var cache = [Int](repeating: 0, count: 101)

cache[1] = 1
cache[2] = 1

//피보나치 수열
func fibo(_ n: Int) -> Int {
	if cache[n] != 0 {
    	return cache[n]
    }
    
    cache[n] = fibo(n-1) + fibo(n-2)
    return cache[n]
}