[알고리즘] 병합 정렬 (Merge Sort)

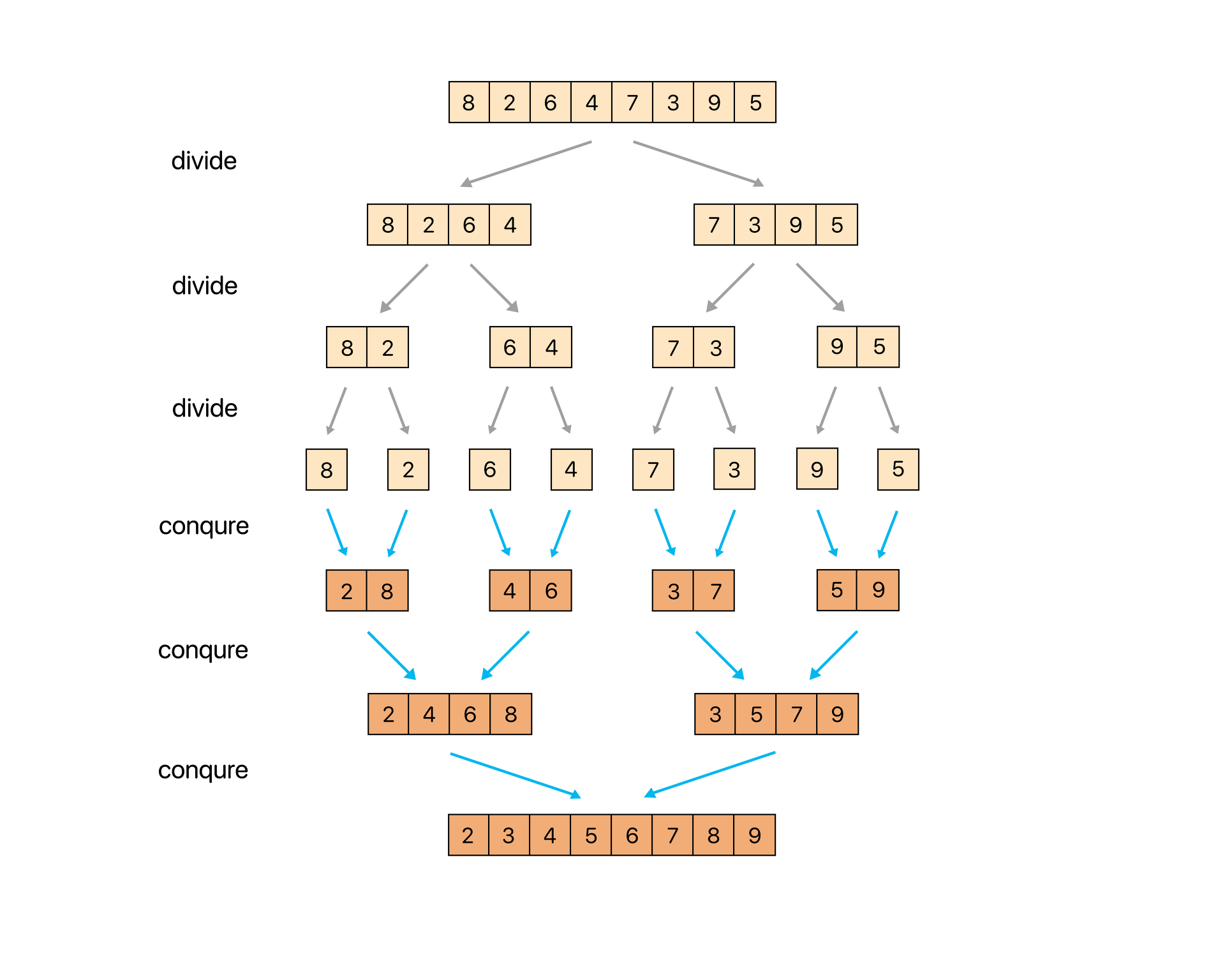
병합 정렬의 개념

병합정렬은 분할정복 알고리즘을 기반으로 정렬되는 방식이다.
병합 정렬은 우선 입력을 반으로 나눈뒤 전반부와 후반부를 각각 독립적으로 정렬하여 마지막으로 정렬된 두 부분을 합쳐서 정렬된 리스트를 얻는다.
이때 전반부와 후반부를 정렬할 때에도 반으로 나누어 정렬한 뒤 병합하는 방식을 이용한다.

요약하자면 병합정렬은 원래 크기를 절반으로 나눈 문제를 2개 푼 다음 이들을 병합하는 작업을 재귀적으로 반복한다.

병합정렬의 전체적인 과정은 다음과 같다.

• 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
• 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
• 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.

병합 정렬의 장단점

장점

• 안정적인 정렬 방법
• 데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. ($O(nlog₂n)$로 동일)
• 만약 레코드를 Linked List로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
• 제자리 정렬(in-place sorting)로 구현할 수 있다.
• 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 병합 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.

단점

• 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.
• 제자리 정렬(in-place sorting)이 아니다.
• 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.

시간복잡도

구현

#include <iostream>
#include <vector>
using namespace std;

vector<int> temp(7);
vector<int> arr = {38, 27, 43, 9, 3, 82, 10};

void merge(int start, int end) {
  int mid = (start + end) / 2;
  // lIdx: 왼쪽 부분배열의 인덱스, rIdx: 오른쪽 부분배열의 인덱스, k: 현재까지 병합 한 인덱스
  int lIdx = start, rIdx = mid + 1, k = start;

  while (k <= end) {
    if (lIdx > mid) {
      temp[k++] = arr[rIdx++];
      continue;
    }
    if (rIdx > end) {
      temp[k++] = arr[lIdx++];
      continue;
    }
    if (arr[lIdx] <= arr[rIdx])
      temp[k++] = arr[lIdx++];
    else
      temp[k++] = arr[rIdx++];
  }
  for (int i = start; i <= end; i++) arr[i] = temp[i];
}

// 더 이상 분할 되지 않을 때까지 분할한 후 merge 함수를 호출하여 병합한다.
void merge_sort(int start, int end) {
  if (start >= end) return;
  int mid = (start + end) / 2;
  merge_sort(start, mid);
  merge_sort(mid + 1, end);
  merge(start, end);
}
// 모든 원소 출력
void print() {
  for (const int &n : arr) cout << n << ' ';
}

int main() {
  // 병합정렬 수행
  merge_sort(0, 6);
  // 결과 출력 : 3 9 10 27 38 43 82
  print();

  return 0;
}