[알고리즘] 시간복잡도와 Big-O 표기법

어떤 문제를 해결하는데 있어서 나오는 알고리즘은 다양할 수 있다.
간단한 예로 주어진 정수 n의 절대값을 구하라는 문제가 있을 때,

1. 정수 n을 제곱한 뒤, 그 값에 다시 루트를 씌운다.
2. 정수 n이 음수인지 확인하고, 조건이 참이면 그 값에 -1을 곱한다.

이처럼 간단한 문제에서도 다양한 풀이 방법이 존재한다.
다양한 풀이 방법들 중 어느 알고리즘이 더 좋은지 분석하기 위해 복잡도를 정의하고 계산한다.
즉, 복잡도 계산은 가장 빠르게 실행되는 알고리즘을 찾는 방법이라고 볼 수 있다.

알고리즘 복잡도(Complexity) 표현 방식

알고리즘의 복잡도를 표현하는 방식에는 크게 두 가지가 있다.

• 시간 복잡도
  문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가리킨다.
  쉽게 말해 알고리즘의 실행 속도(성능)을 계산하는 표현 방법이다.

• 공간 복잡도
  알고리즘에서 사용하는 메모리 크기.
  과거에는 메모리 가격이 비싸기 때문에 얼마나 적은 메모리를 차지하면서 알고리즘이 수행되는지가 중요했었다. 현재는 공간 복잡도보다 시간 복잡도가 더 중요하기 때문에 시간 복잡도에 대해 이해하고 계산할 수 있어야 한다.

알고리즘 시간 복잡도에 영향을 주는 주요 요소는 반복문이다. 반복되는 횟수가 많아질수록, 여러 반복문이 중첩될수록 시간 복잡도는 올라가게 된다.

알고리즘 성능 표기법

• Big-O 표기법: O(n)
  알고리즘 최악의 실행 시간을 표기한다. 가장 많이 그리고 가장 일반적으로 사용하는 표기법이다. 아무리 최악의 상황이라도 최소 이정도의 성능은 보장한다는 의미이기 때문에 Big-O 표기법을 가장 많이 쓴다.

• Big-Ω 표기법: Ω(n)
  오메가 표기법은 알고리즘 최상의 실행 시간을 표기한다.

• Big-θ 표기법: θ(n)
  세타 표기법은 알고리즘 평균 실행 시간을 표기한다.

이 중 Big-O(빅 오) 표기법을 가장 많이 쓴다.

Big-O 표기법

O(n)으로 표기하고 입력되는 n에 따라 결정되는 시간 복잡도 함수이다.
$O(1)$, $O(logn)$, $O(n)$, $O(nlogn)$, $O(n^2)$, $O(2^n)$, $O(n!)$ 등으로 표기한다.
입력되는 n의 크기에 따라 시간 복잡도가 기하급수적으로 늘어날 수 있다.

시간 복잡도 크기 순서
$O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)$

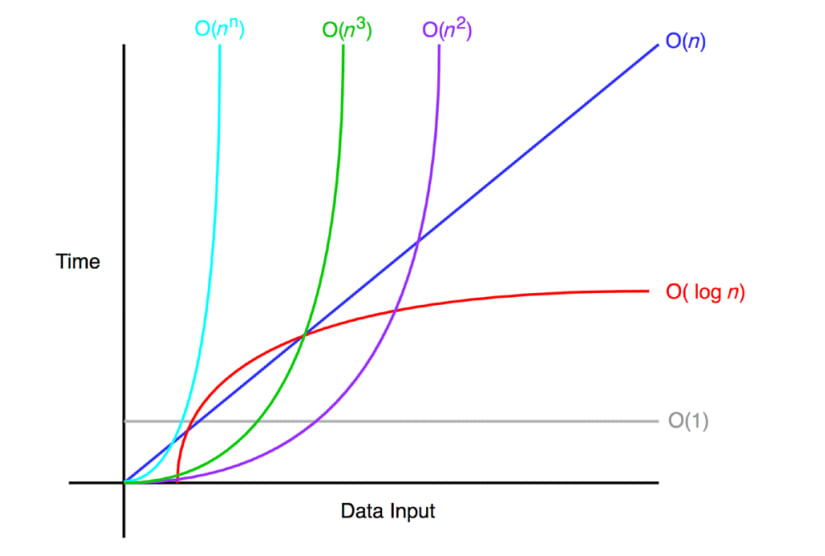
시간복잡도 계산

시간복잡도에서 중요한 것은 가장 큰 영향을 미치는 n의 단위이다.

$1$                            $O(1)$ -->  상수
$2n + 20$              $O(n)$ -->  n이 가장 큰영향을 미친다.
$3n^2$                       $O(n^2)$ -->  $n^2$이 가장 큰영향을 미친다.