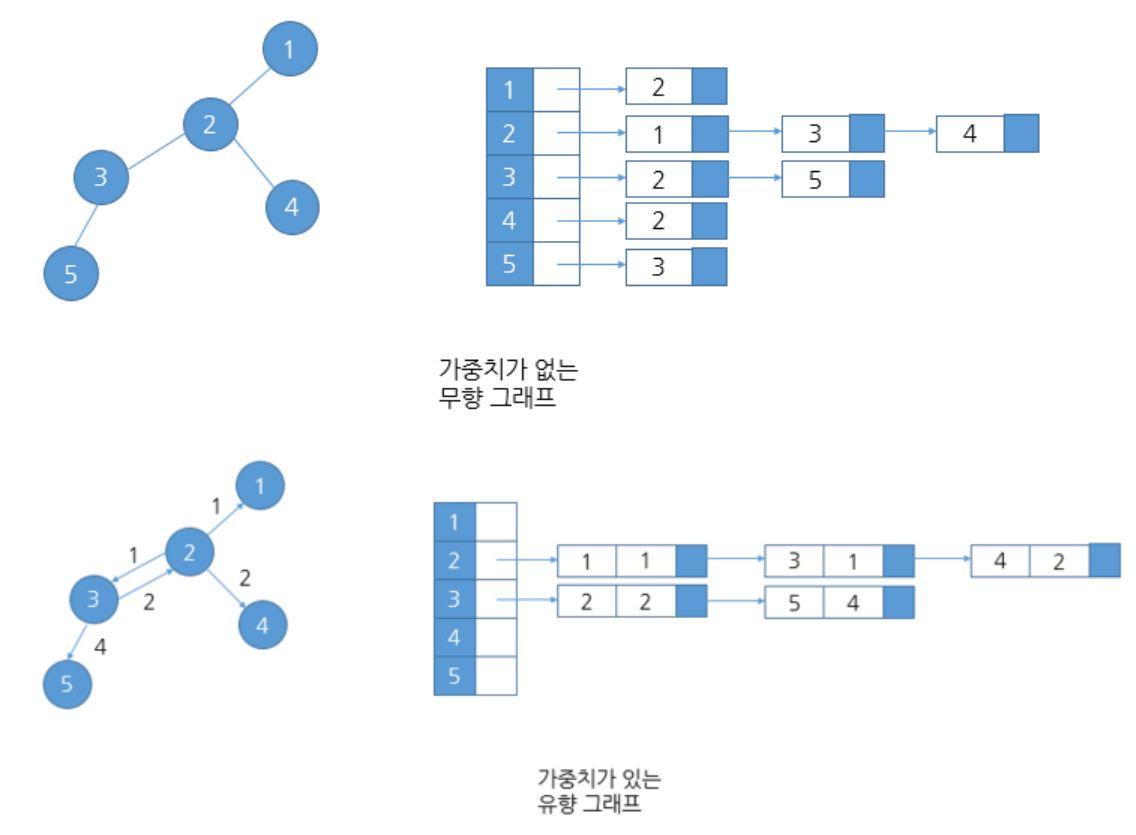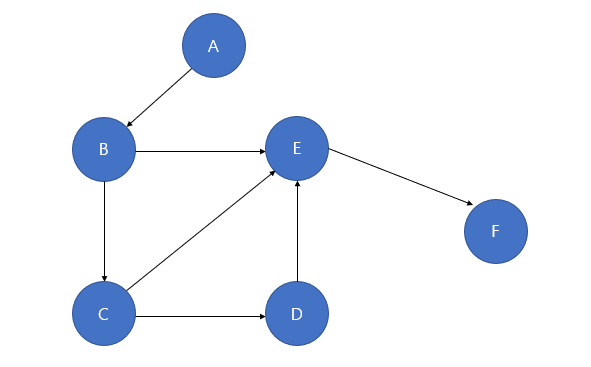
그래프는 노드(N, node)와 그 노드를 연결하는 간선(E, edge)을 하나로 모아 놓은 자료 구조로 원소간의 다대다 관계를 표현한 자료구조이다.
그래프 관련 용어
- vertex (정점) : 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소이다.
- edge (간선) : 링크(link)라고도 하며 정점 간의 관계를 나타낸다.
- degree (차수) : 정점에 연결된 간선의 수
- in-degree : 내부로 향하는 간선의 수
- out-degree : 외부로 향하는 간선의 수
- cycle : 시작 정점과 종료 정점이 같은 단순 경로
- path (경로) : 간선을 따라갈 수 있는 길
- length (경로의 길이): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로 (simple path): 경로 중에서 반복되는 간선이 없는 경로
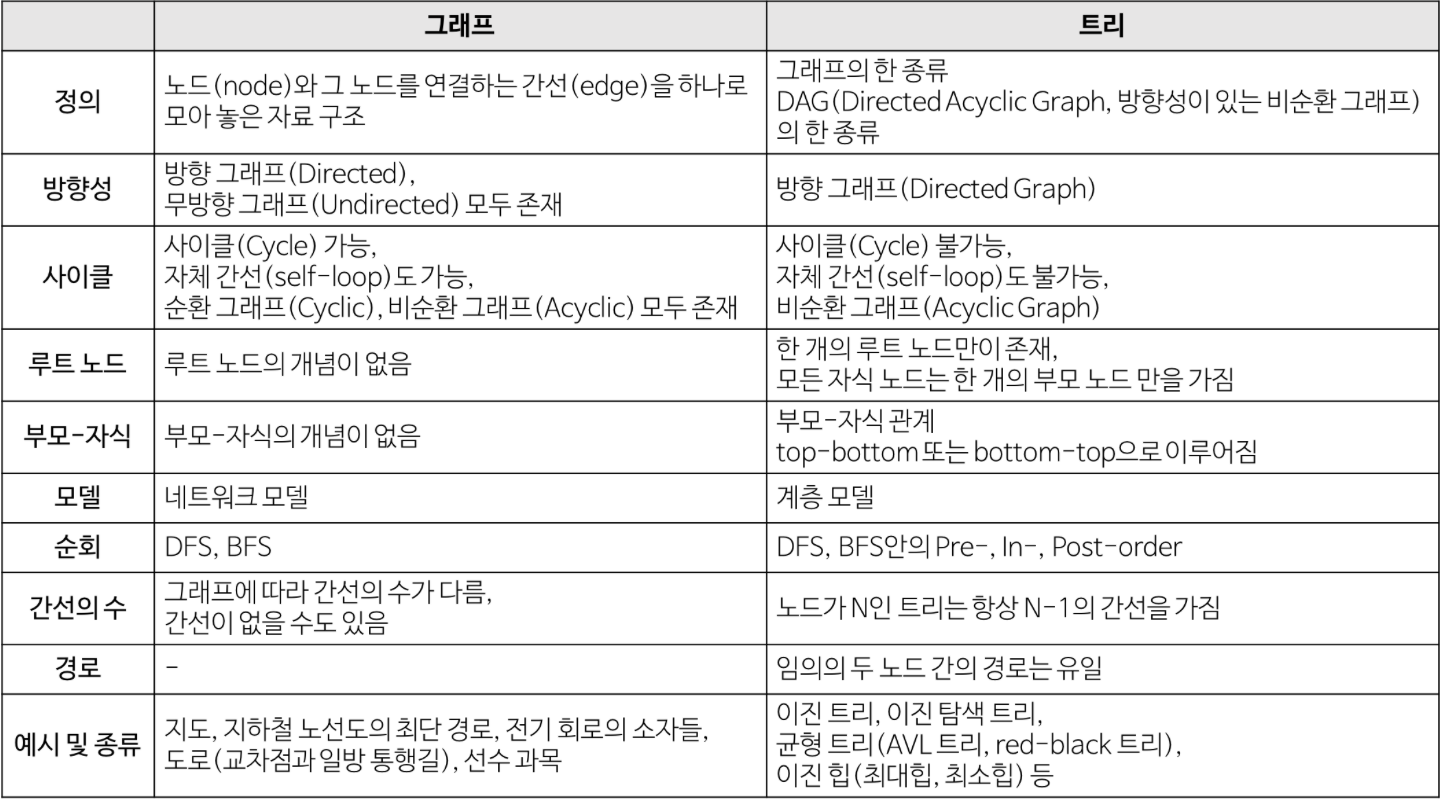
그래프와 트리의 차이점
트리는 그래프의 한 종류이며, 그 중 사이클(cycle)이 허용되지 않는 그래프를 말한다.
또한 트리는 루트 노드가 존재하지만 그래프에는 루트 노드의 개념이 없다.
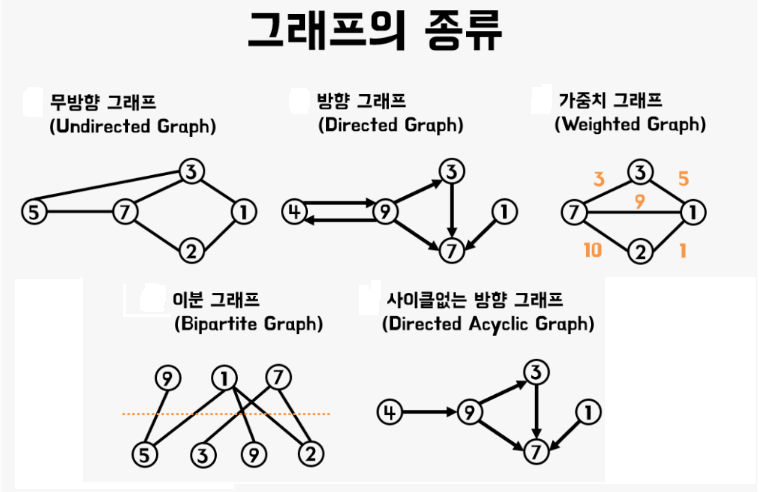
그래프 종류
-
무방향 그래프(Undirected Graph)
간선에 방향이 없는 그래프이다
노드와 간선으로 이루어져 있으며, 노드 사이의 관계는 양방향이다. -
방향 그래프(Directed Graph)
간선에 방향이 있는 그래프이다.
노드와 간선으로 이루어져 있으며, 노드 사이의 관계는 일방향이다. -
가중치 그래프(Weighted Graph)
간선에 가중치(weight)가 있는 그래프이다.
가중치는 간선의 비용, 거리, 시간 등을 나타낸다. -
이분 그래프(Bipartite Graph)
무방향 그래프에서, 노드를 두 그룹으로 나누었을 때, 같은 그룹 내의 노드는 서로 인접하지 않고, 다른 그룹의 노드와만 인접하는 그래프이다. -
비순환 그래프(Acyclic Graph)
사이클이 없는 그래프이다.
방향 그래프에서, 유향 비순환 그래프(Directed Acyclic Graph, DAG)라고도 한다.
-
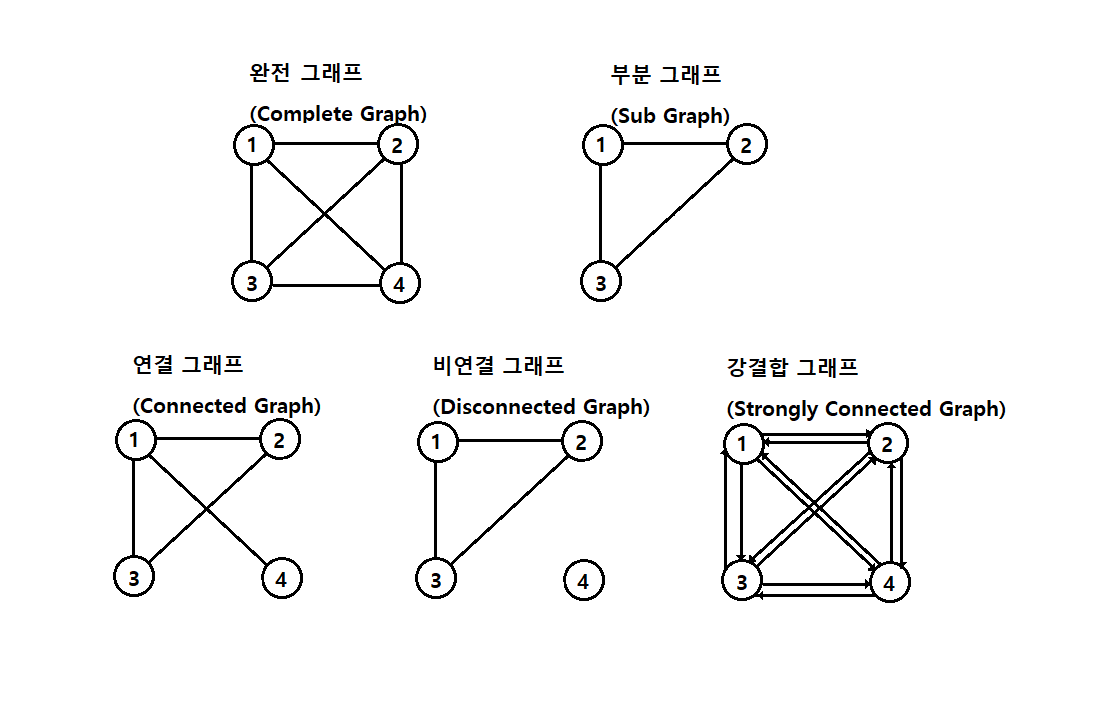
완전 그래프(Complete Graph)
모든 노드가 서로 연결된 그래프이다.
노드 수가 n일 때, 간선 수는 n(n-1)/2 입니다.
완전 그래프는 항상 연결그래프를 포함한다. -
부분 그래프(Subgraph)
주어진 그래프의 일부 노드와 간선으로 이루어진 그래프이다. -
연결 그래프(Connected Graph)
무방향 그래프에서, 모든 노드 사이에 경로가 존재하는 그래프이다. -
비연결 그래프(Disconnected Graph)
무방향 그래프에서, 연결 그래프가 아닌 그래프이다. -
강결합 그래프(Strongly Connected Graph)
방향 그래프에서, 모든 노드 사이에 양방향 경로가 존재하는 그래프이다.
구현
그래프를 구현하는 방법에는 배열을 사용하는 방법과 연결리스트를 사용하는 방법이 있다.
인접행렬은 정점과 간선의 정보를 행렬로 표현하는 방법으로 간선과 상관없이 모든 정점을 표현해야 하기 때문에 정점의 수가 많을수록 메모리 사용량이 늘어난다.
반면에 인접리스트는 정점과 간서의 정보를 리스트로 표현하는 방법으로 연결된 것만 표시하면 되기 때문에 인접행렬에 비해 간단하다.
인접행렬 (Adjacency matrix)
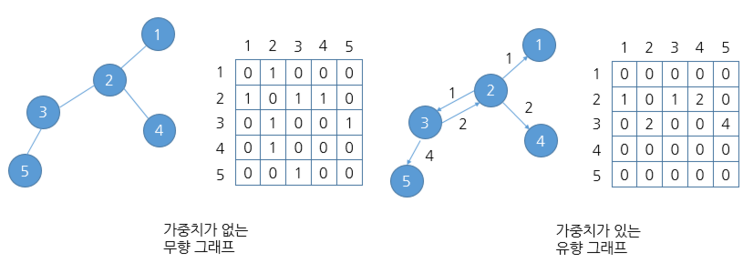노드의 개수가 n이라면 n*n 형태의 2차원 배열로 그래프의 연결 관계를 표현한다.
인접 행렬에서 행과 열은 노드를 의미하며, 각각의 원소들은 노드 간의 간선을 나타낸다.
adj[i][j] : 노드 i에서 노드 j로 가는 간선이 있으면 1, 아니면 0
장점
- 두 노드의 간선 정보를 확인하는것이 빠르다. O(1)
- 새로운 간선을 추가하고 제거하는것이 빠르다. O(1)
단점
- 간선의 개수와 상관없이 배열의 크기는 항상 N*N 개이다. (N은 노드의 개수)
- 위 그래프에서 노드가 4개이기 때문에 배열의 원소 개수는 (4 x 4) = 24 개
O(N^2) 의 메모리를 사용 - 특정한 노드에 인접한 노드를 찾기위해서 모든 노드를 순회해야 한다.
- 노드를 추가 하거나 제거하는데 오래 걸린다. O(N^2)
- 그래프의 모든 간선의 수를 찾는데 O(N^2) 인접 행렬은 상대적으로 노드의 개수가 적고 간선의 수가 많을때 사용하는것이 좋다고 할 수 있다. 따라서 간선이 많은 밀집 그래프(Dense Graph)에 적합하다.
코드
#include <iostream>
using namespace std;
#define MAX_VTXS 256 // 최대 정점 개수
class AdjMatGraph{
private:
int size; // 정점의 개수
char vertices[MAX_VTXS]; // 정점의 이름
int adjMat[MAX_VTXS][MAX_VTXS]; // 인접 행렬
public:
AdjMatGraph(){
reset();
}
~AdjMatGraph(){}
char getVertex(int i){
return vertices[i];
}
int getEdge(int i, int j){
return adjMat[i][j];
}
void setEdge(int i, int j, int val){
adjMat[i][j] = val;
}
// 그래프 초기화
void reset(){
for(int i=0; i<MAX_VTXS; i++){
for(int j=0; j<MAX_VTXS; j++){
setEdge(i, j, 0);
}
}
size = 0;
}
// 정점 삽입
void insertVertex(char name){
if(isFull()){
cout << "Graph vertex full error" << endl;
return;
}
vertices[size++] = name;
}
// 간선 삽입 (무방향 그래프)
void insertEdge(int u, int v){
setEdge(u, v, 1); // 가중치 그래프에서는 1이 아닌 가중치 삽입
setEdge(v, u, 1); // 방향 그래프에서는 삭제 (<u,v>만 존재)
}
// 그래프 정보 출력
void display(){
cout << "vertex size : " << size << endl;
cout << " ";
for(int i=0; i<size; i++){
cout << getVertex(i) << " ";
}
cout << endl;
for(int i=0; i<size; i++){
cout << getVertex(i) << " : ";
for(int j=0; j<size; j++){
cout << getEdge(i, j) << " ";
}
cout << endl;
}
}
bool isEmpty(){
return size == 0;
}
bool isFull(){
return size >= MAX_VTXS;
}
};
int main(){
AdjMatGraph graph;
// 정점 삽입 (A, B, C, D)
graph.insertVertex('A'); // 0
graph.insertVertex('B'); // 1
graph.insertVertex('C'); // 2
graph.insertVertex('D'); // 3
// 간선 삽입
graph.insertEdge(0, 1); // A->B
graph.insertEdge(0, 2); // A->C
graph.insertEdge(0, 3); // A->D
graph.insertEdge(2, 3); // C->D
graph.display();
return 0;
}인접리스트 (Adjacency matrix)
그래프의 각 노드에 인접한 노드들을 연결리스트(Linked List)로 표현하는 방법이다.
즉, 노드의 개수만큼 인접리스트가 존재하며, 각각의 인접리스트에는 인접한 노드 정보가 저장된다. 그래프는 각 인접리스트에 대한 헤드포인터를 배열로 갖는다.
헤드포인터 : 연결 리스트의 맨 처음 노드를 가리키는 포인터
장점
- 존재하는 간선만 관리하므로 보다 메모리 사용이 효율적이다.
단점
- 두 노드를 연결하는 간선을 조회하거나 노드의 차수를 알기 위해서는 노드의 인접 리스트를 탐색해야 하므로 노드의 차수만큼의 시간이 필요하다.
코드
#include <iostream>
using namespace std;
#define MAX_VTXS 256 // 최대 정점 개수
struct Node{
private:
int id; // vertex id
Node* link; // next node's pointer
public:
Node(int _id, Node* _link){
id = _id;
link = _link;
}
~Node(){};
// getter/setter
int getId(){
return id;
}
void setId(int _id){
id = _id;
}
Node* getLink(){
return link;
}
void setLink(Node* _link){
link = _link;
}
};
class AdjListGraph{
private:
int size; // 정점의 개수
char vertices[MAX_VTXS]; // 정점의 이름
Node* adjList[MAX_VTXS]; // 인접 리스트
public:
AdjListGraph(){
size = 0;
}
~AdjListGraph(){}
char getVertex(int i){
return vertices[i];
}
// 그래프 초기화
void reset(){
for(int i=0; i<size; i++){
if(adjList[i] != NULL){
delete adjList[i];
}
}
size = 0;
}
// 정점 삽입
void insertVertex(char name){
if(isFull()){
cout << "Graph vertex full error" << endl;
return;
}
vertices[size] = name;
adjList[size++] = NULL;
}
// 간선 삽입 (무방향 그래프)
void insertEdge(int u, int v){
// 인접리스트에 추가
adjList[u] = new Node(v, adjList[u]); // 새로운 노드로 head pointer가 바뀜 (새로운 node는 기존의 head pointer를 link로 함)
adjList[v] = new Node(u, adjList[v]); // 방향 그래프에서는 삭제 (<u,v>만 존재)
}
// 그래프 정보 출력
void display(){
cout << "vertex size : " << size << endl;
for(int i=0; i<size; i++){
cout << getVertex(i) << " : ";
Node* head = adjList[i];
while(head != NULL){
cout << getVertex(head->getId()) << " ";
head = head->getLink();
}
cout << endl;
}
}
// 'v'번째 정점의 인접 정점 리스트 반환
Node* adjacent(int v){
return adjList[v];
}
bool isEmpty(){
return size == 0;
}
bool isFull(){
return size >= MAX_VTXS;
}
};
int main(){
AdjListGraph graph;
// 정점 삽입 (A, B, C, D)
graph.insertVertex('A'); // 0
graph.insertVertex('B'); // 1
graph.insertVertex('C'); // 2
graph.insertVertex('D'); // 3
// 간선 삽입
graph.insertEdge(0, 1); // A->B
graph.insertEdge(0, 2); // A->C
graph.insertEdge(0, 3); // A->D
graph.insertEdge(2, 3); // C->D
graph.display();
return 0;
}