Programmers: 정수 삼각형

문제

• Programmers 동적 계획법 LV3, 정수 삼각형
  

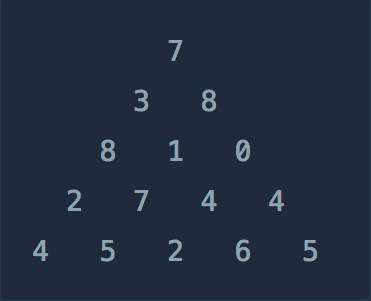
입력을 보면..

• 주어진 입력들을 보면, 위-아래로 뻗어나가는 형식
• 특히 C++은 배열이 아니라 vector<vector<int>> 형식으로 나타내므로 작업 시, 인덱스 넘어가는것 조심!
• 아래 표는 실제 인풋으로 들어오는 배열을 엑셀로 표시한 내용입니다!
  

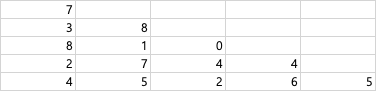
핵심!

• 이 문제는 동적 프로그래밍 문제
  • 즉, 계산을 불필요하게 다 하는 것이 아니라, 썼던거 간단하게 재활용 해서 시간을 아끼자는 취지!
• 문제 정의에 의해서 위 표의 4번째 행[2 7 4 4] 을 기준으로,
  • 2는 4와 5를 더할 수 있고,
  • 7은 5와 2를 더할 수 있고,
  • 4는 2와 6을 더할 수 있고,
  • 4는 6과 5를 더할 수 있다.
  • 문제는 "가장 큰" 수를 최종적으로 구하자는 것이니, 할 수 있는 선택 중, 최대로 큰 수를 구하자는게 이 문제의 핵심이다.
  • 가령, 2, 7, 4, 4를 계속 기준으로 삼아
    • max(4, 5) + 2,
    • max(2, 5) + 7,
    • max(2, 6) + 4,
    • max(6, 5) + 4
  • 형식이 되는 것이다.
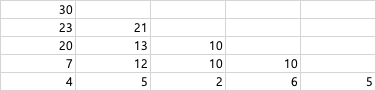
• 일반화 시키면, 첫 줄은 그냥 인풋 그대로를 가져다 쓰고, 그 윗줄부터는 자신의 아래 원소와, 아래-오른쪽 원소를 더해버리기~가 되는 것이다!
• 일반화 시킨 식을 기준으로 표를 채워가고, 표의 가장 위-첫 원소[0][0]을 리턴하면 성공!
• 아래 표는 일반화 시킨 dp배열을 손[엑셀]로 작성해 본 표 입니다.
  

코드

int solution(vector<vector<int>> triangle) {
    // Init DP Vector
    size_t bottom_size = triangle[triangle.size() - 1].size();
    size_t bottom_index = triangle.size() - 1;
    
    vector<vector<int>> dp(triangle.size());
    dp[triangle.size() - 1].reserve(bottom_size);
    
    // Init Last Line
    for (int i = 0; i < bottom_size; i++) {
        dp[bottom_index][i] = triangle[bottom_index][i];
    }
    bottom_size--;
    
    // Bottom-Up
    for (int i = bottom_index-1; i >= 0; i--) {
        for (int j = 0; j < bottom_size; j++) {
            dp[i].push_back(max(dp[i+1][j], dp[i+1][j+1]) + triangle[i][j]);
        }
        bottom_size--;
    }

    return dp[0][0];
}