Graph

그래프

정점(Vertex or Node)와 간선(Edge)으로 이루어진 자료구조

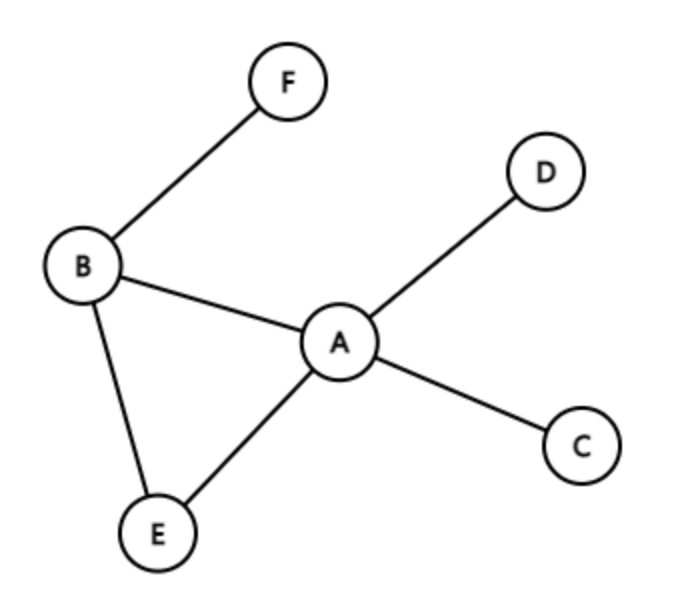
구성요소

• 노드(Vertex)

  그래프에서 데이터나 객체를 나타내는 점
  Ex) 사람, 도시 등

• 엣지(Edge)

  두 노드를 연결하는 선으로, 노드 간의 관계나 연결을 나타냄
  Ex) 도로, 친구 관계, 하이퍼링크 등

• 가중치(Weight)

  엣지에 부여된 값으로, 두 노드 간의 거리, 비용, 시간 등을 나타냄
  Ex) 도로의 길이, 통화 비용, 전송 시간 등

용어

• 차수(Degree)

종류

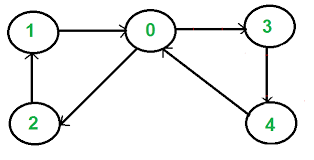
• 방향 그래프
  

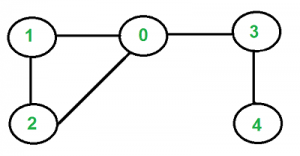
• 무방향 그래프
  

• 완전 그래프
  

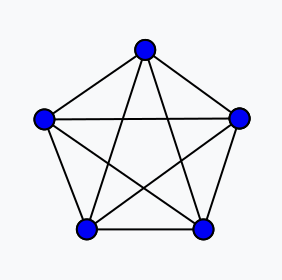
• 부분 그래프
  

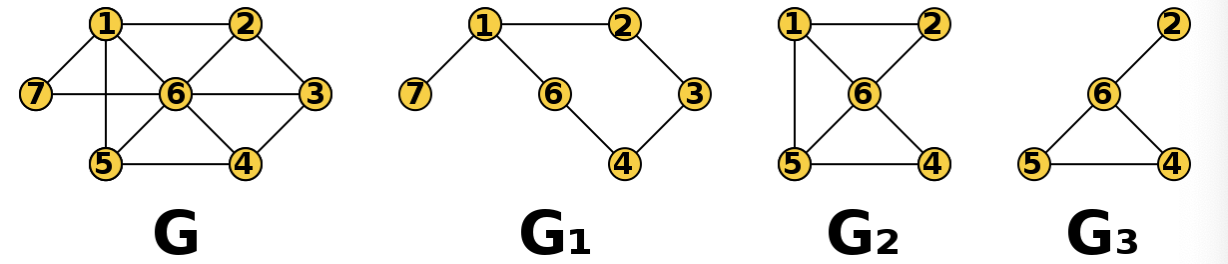
• 가중 그래프
  

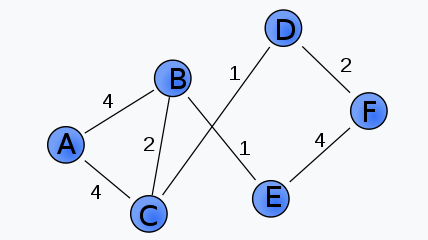
• 연결 그래프
  

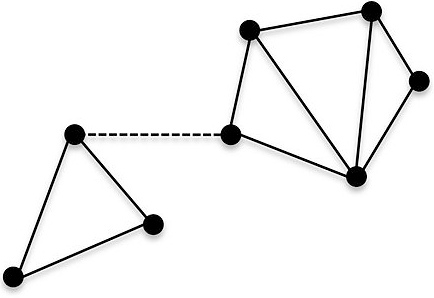
표현방법

무방향 그래프

A - B
|   |
C - D


방향 그래프

A -> B
|    |
v    v
C <- D

위의 그래프를 인접 행렬과 인접 리스트로 표현해보면 아래와 같다.

• 인접 행렬

  무방향 그래프
      A B C D
  A [ 0 1 1 0 ]
  B [ 1 0 0 1 ]
  C [ 1 0 0 1 ]
  D [ 0 1 1 0 ]
  
  방향 그래프
  
      A B C D
  A [ 0 1 1 0 ]
  B [ 0 0 0 1 ]
  C [ 0 0 0 0 ]
  D [ 0 0 1 0 ]
  

• 인접 리스트

  무방향 그래프
  A: B, C
  B: A, D
  C: A, D
  D: B, C
  
  방향 그래프
  A: B, C
  B: D
  C: 
  D: C
  

특징

• 루트 노드, 부모-자식관계 개념이 없음

• 2개 이상의 경로가 가능

• 루프가 가능

장점

• 유연한 모델링

  소셜 네트워크의 친구 관계, 도로 네트워크 등 복잡한 관계나 연결을 직관적으로 표현할 수 있다.

• 경로 탐색과 최단 경로

  다익스트라 알고리즘, Astar알고리즘 등의 그래프 알고리즘을 통해 최단 경로 탐색, 경로 존재 여부 확인 등의 문제를 효율적으로 해결할 수 있다.

• 네트워크 구조 표현

  인터넷, 전력망, 교통 시스템 등 다양한 네트워크 구조를 표현하고 분석할 수 있다.

단점

• 복잡성

  그래프의 크기가 커질수록 메모리 사용량과 연산 시간이 증가하여, 효율적인 처리가 어려울 수 있다.

• 구현의 복잡성

  특정 그래프 알고리즘은 구현과 최적화가 어렵고 특히 가중치 그래프나 방향 그래프의 경우 복잡한 연산이 필요하다.

• 높은 공간 복잡도
  인접 행렬은 $O(V^2)$, 인접 리스트는 $O(V+E)$의 공간 복잡도를 가지기 때문에 데이터 저장시 비효율적일 수 있다.

그래프의 활용

• 네트워크 분석

• 경로 탐색

• 데이터 구조 표현

---

그래프의 탐색

• 깊이 우선 탐색 (DFS)

• 넓이 우선 탐색 (BFS)

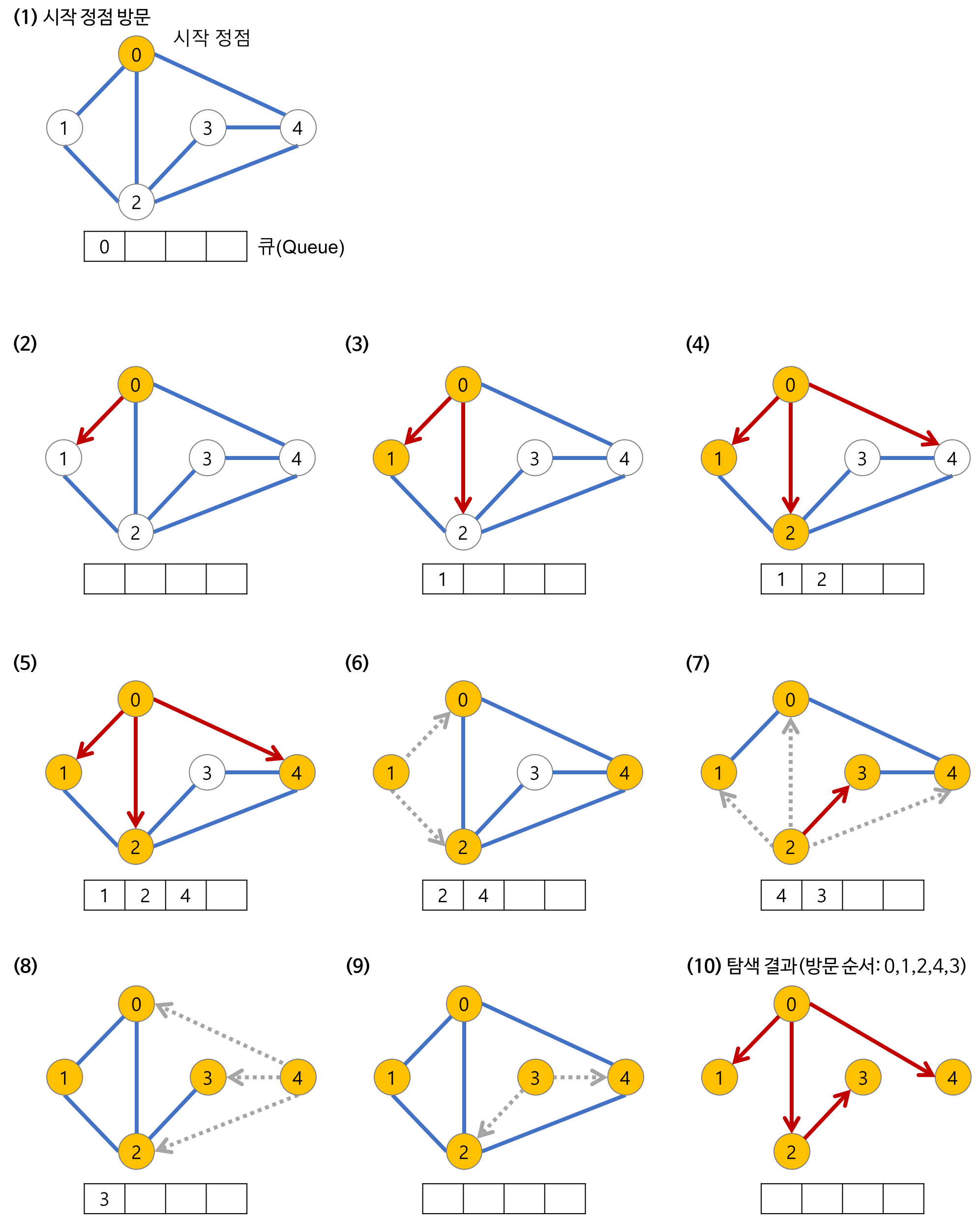
깊이 우선 탐색(Depth First Search)

그래프 완전 탐색 기법 중 하나로, 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘

• 주로 스택을 사용

• 모든 노드를 방문하고자 할 때 사용

• BFS보다 좀 더 간단하며 단순 검색 속도는 BFS보다 조금 느림

DFS 과정

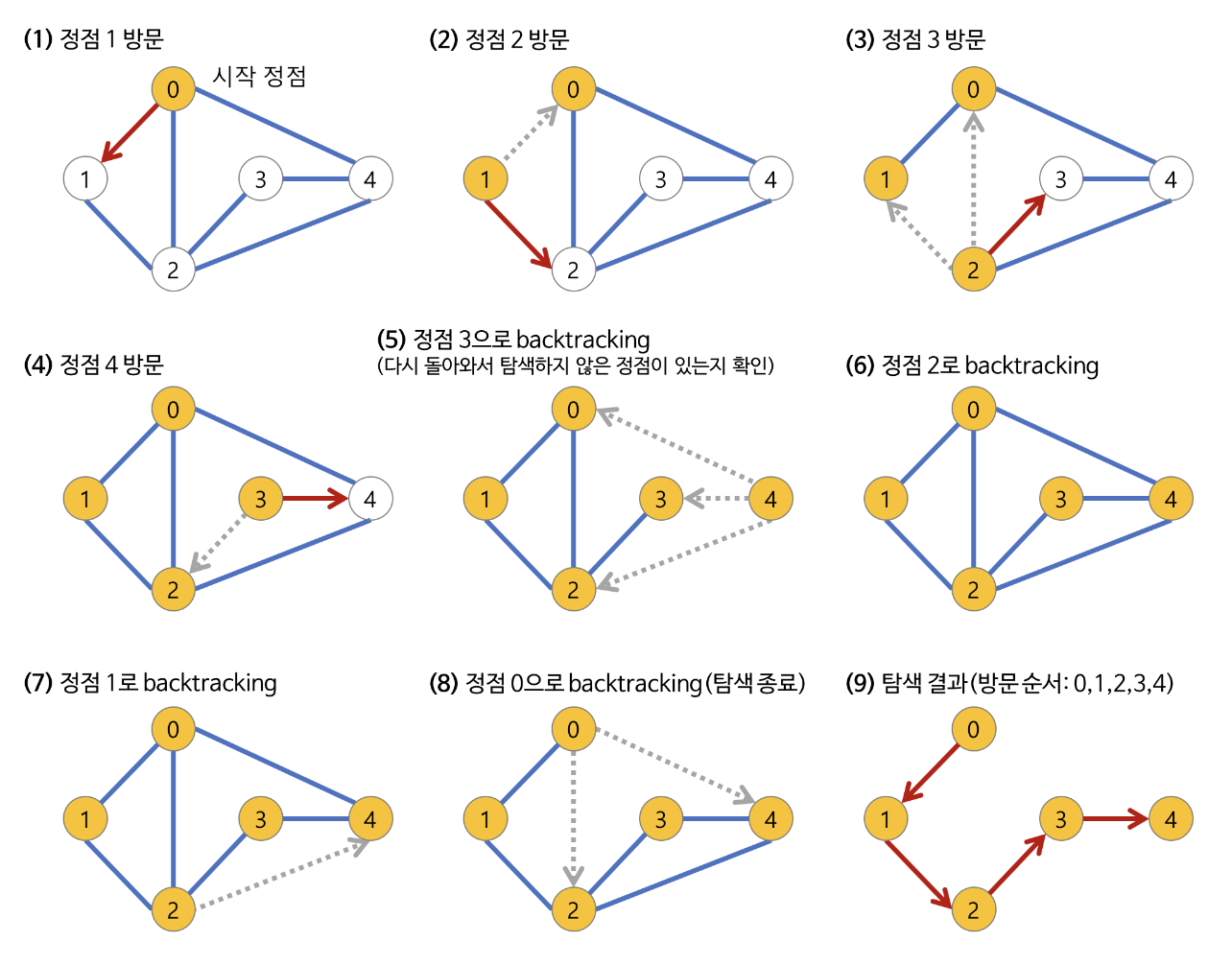
a 노드(시작 노드)를 방문한다.

• 방문한 노드는 방문했다고 표시한다.

a와 인접한 노드들을 차례로 순회한다.

• a와 인접한 노드가 없다면 종료한다.

a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.

• b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 노드들을 방문한다.

b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.

• 즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문할 수 있다는 뜻이다.

아직 방문이 안 된 정점이 없으면 종료한다. 있으면 다시 그 정점을 시작 정점으로 DFS를 시작한다.

---

넓이 우선 탐색 (Breadth-First Search)

그래프의 완전 탐색 알고리즘 중 하나로, 시작 정점에서 시작하여 인접한 모든 정점을 탐색한 후 다음 정점을 탐색하는 알고리즘.

• 주로 큐를 사용

• 무방향 그래프에서 사용시 최단 경로를 찾을 수 있음

• 구현이 비교적 간단하며 DFS에 비해 메모리를 효율적으로 사용함. 단, 깊이가 깊다면 더 많은 메모리를 사용함

BFS 과정

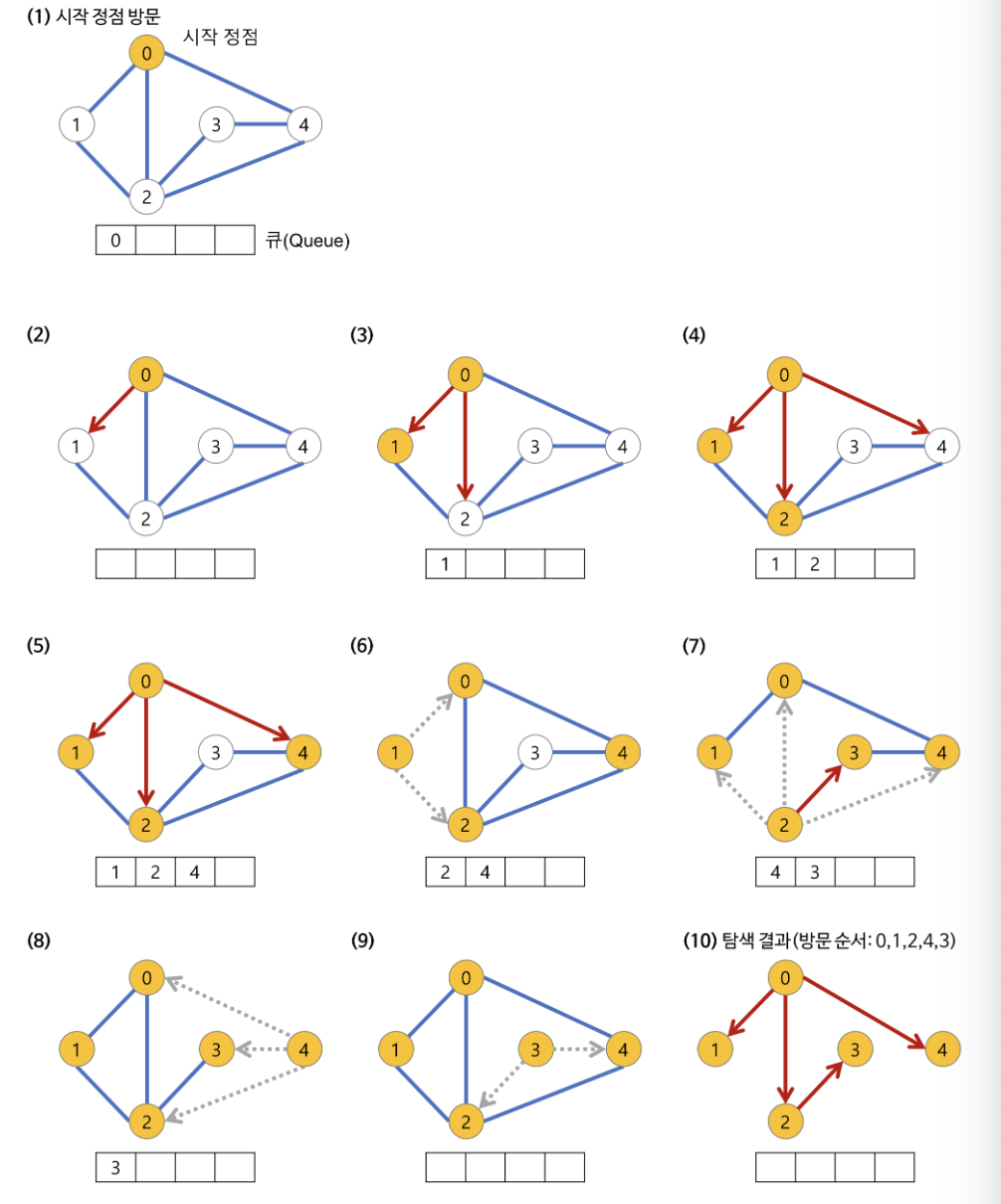
시작노드를 방문하고 방문한 노드를 체크한다.

• 큐에 시작노드의 이웃 노드들을 삽입힌다.

방문처리가 모두 끝났다면 큐에서 노드를 하나 꺼내 해당 노드의 이웃들을 방문 처리한다.

• 인접한 노드가 없다면 다음 노드를 꺼낸다.
• 있다면 해당 노드를 큐에 삽입한다.

큐가 빌 때까지 계속한다.

---

레퍼런스

• 그래프의 개념

• 깊이 우선 탐색이란

• 넓이 우선 탐색이란