Red Black Tree

Red Black Tree

이진 탐색 트리의 일종으로, 기존 이진 탐색 트리가 가진 편향성 문제를 해결하고 평균적인 성능의 확보를 위해 고안된 자가 균형 트리이다.

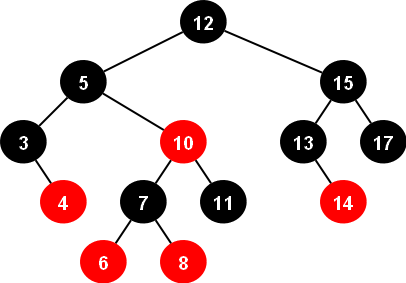
• 기본적으로 이진 탐색 트리
• 스스로 정렬하기 위한 규칙이 추가된 것

이진 탐색 트리의 문제

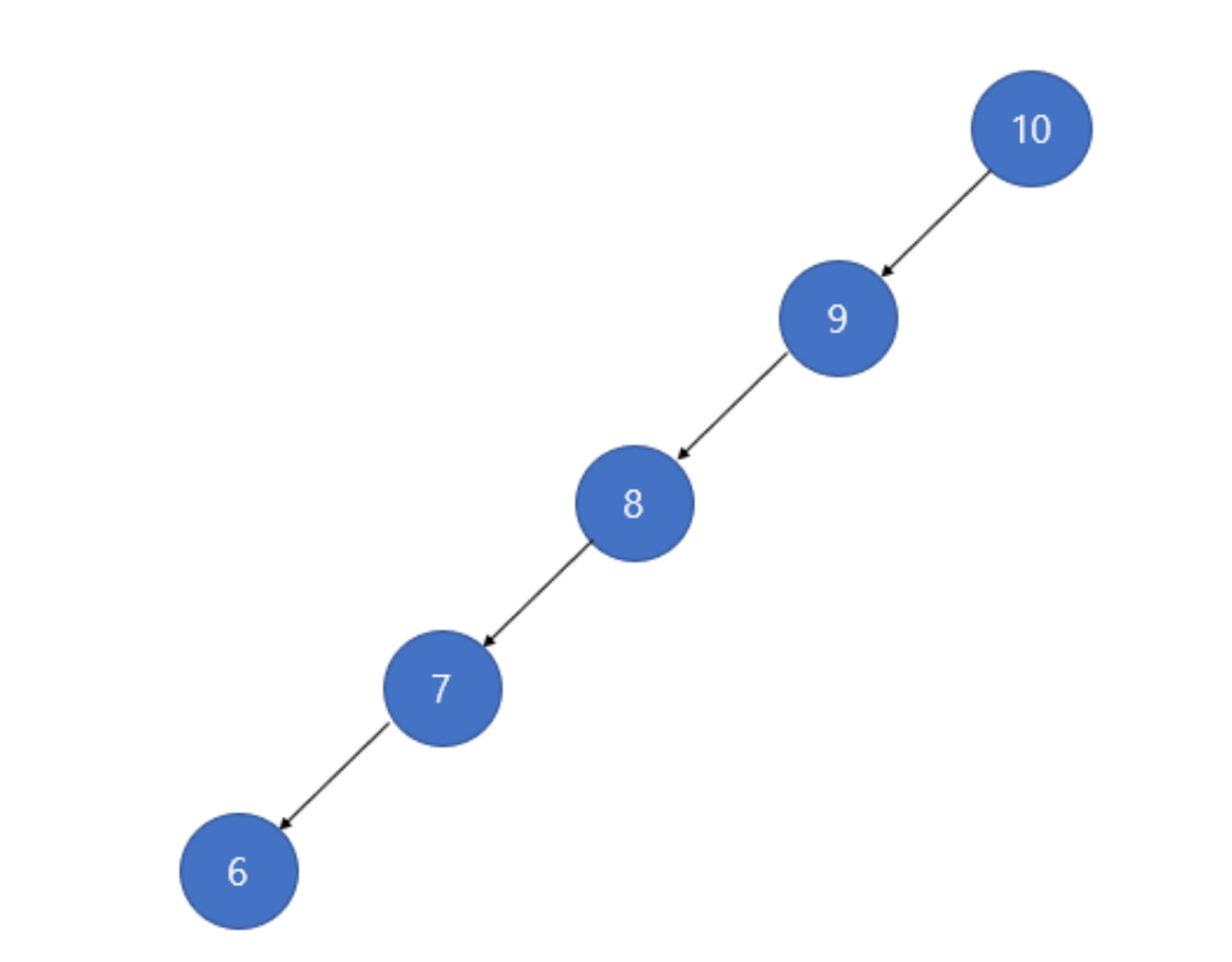
• 편향성 문제

  이진 탐색트리는 값의 크기만 가지고 데이터를 삽입하기 때문에 계속해서 큰 값이나 작은 값만 넣으면 한쪽으로 길게 늘어지는 편향성 문제가 생김

  • 최악의 경우 검색시 전체 요소를 순회해야 한다는 문제(검색 성능 저하) 발생

  -> 최선과 최악일 때의 성능 편차를 줄이고자 고안된 트리가 AVL과 Red Black같은 균형트리

레드블랙과 이진탐색의 시간복잡도

종류	삽입	삽입(최악)	검색	검색(최악)	삭제	삭제(최악)
레드블랙트리	O(log n)	O(log n)	O(log n)	O(log n)	O(log n)	O(log n)
이진탐색트리	O(log n)	O(n)	O(log n)	O(n)	O(log n)	O( n)

이진 탐색트리가 최악일 때 시간 복잡도가 O(n)가지 올라가는 반면, 레드블랙은 지속적으로 균형을 유지하기 때문에 최악의 경우에도 이진 탐색 트리의 장점을 계속해서 가져갈 수 있음

구성요소

• 이진 탐색 트리와 동일한 요소들
  
  
• NIL노드

  NIL노드는 레드블랙 트리의 균형을 맞출 때 null대신 사용하는 말단 노드로, 데이터는 없고 black이라는 색을 가짐

• 노드의 색

  균형을 맞추기 위한 레드블랙 트리의 특징적인 값으로, red, black 두 개의 값으로 이루어짐

• Extra Black

  노드가 삭제될 때 레드블랙 트리의 균형을 유지하기 위한 임시 장치로, 우선 노드에 붙이고 나중에 없애야 하는 값

균형 규칙

• 루트 노드의 색은 black이다.

• 새로 삽입되는 노드의 색은 red이다.

• double red (연속된 노드의 색이 red)가 발생하면 restructuring 또는 recoloring으로 해결한다.

• 리프 노드의 말단에는 색이 black이고 값은 없는 NIL노드가 연결된다.

• 모든 리프 노드로부터 루트 노드까지 거쳐가는 black 노드의 숫자는 같다. (black depth라 부를 예정)

---

삽입

절차

1. 위치 탐색
2. 삽입 처리
3. 균형 유지

• 위치 탐색: 이진 탐색 트리의 규칙대로 삽입할 위치를 찾는다. (루트부터 넣을 값을 비교하여 작으면 좌측, 크면 우측)

• 삽입처리: 이진 탐색 트리와 마찬가지로 찾은 위치가 비어있으면 값을 넣고 부모와 연관관계를 맺어준다.

• 균형유지: double red가 발생했다면, 해결될 때 까지 restructuring 또는 recoloring을 사용한다.

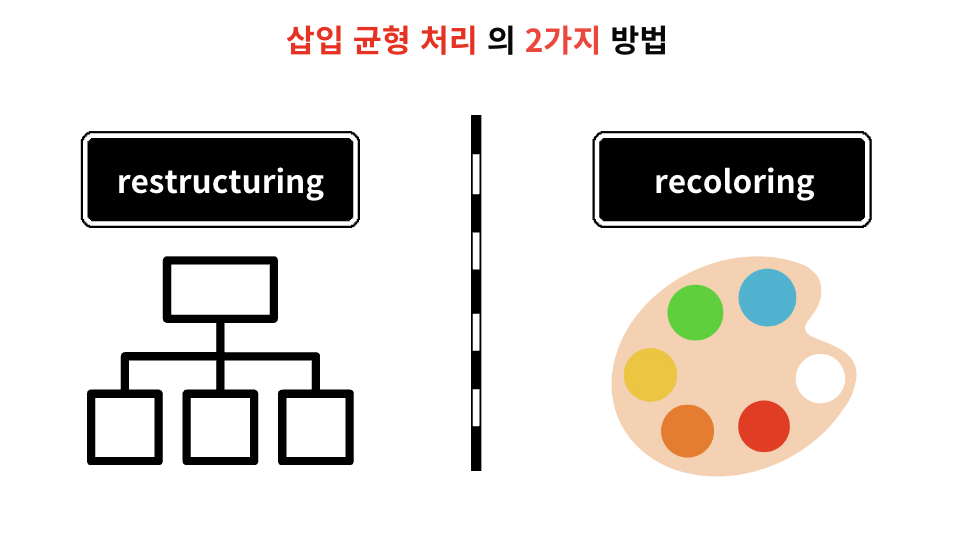
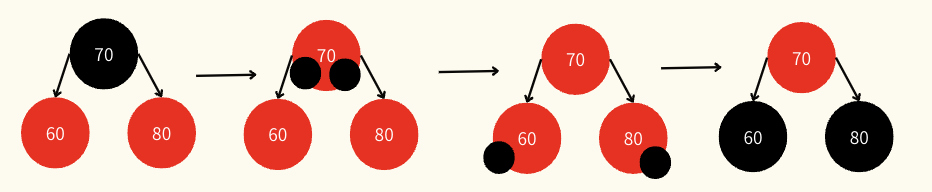
double red가 발생하면 위의 두 가지 방법을 사용하여 해결한다.

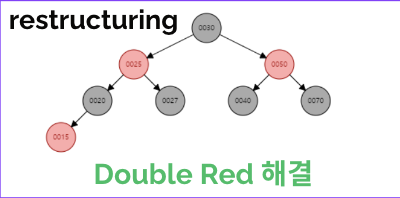
restructuring

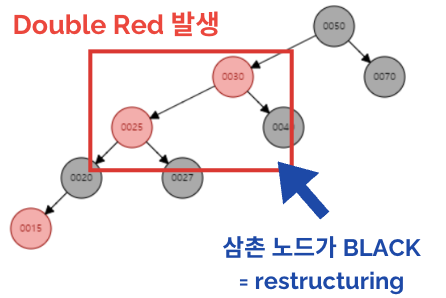
새로 삽입된 노드의 삼촌 노드(부모와 형제)가 Black인 경우

1. 새로운 노드, 부모 노드, 조상 노드를 오름차순 정렬한다
   
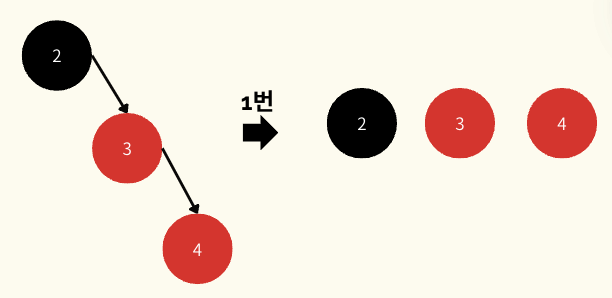
2. 중간 값을 부모로, 나머지 값 중 작은 값을 left, 큰 값을 right로 만든다
   
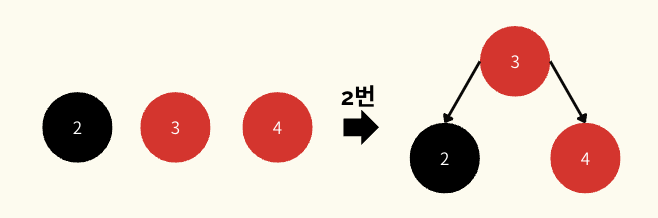
3. 새로 부모가 된 노드를 black으로, 그 자식들을 red로 바꿔준다
   

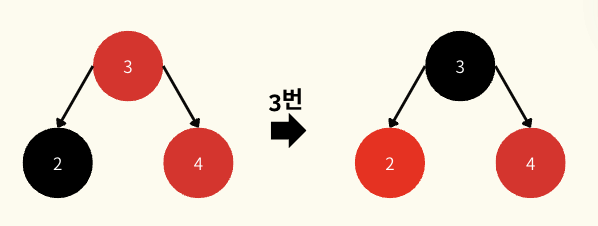
recoloring

새로 삽입된 노드의 삼촌 노드(부모의 형제)가 red인 경우 수행

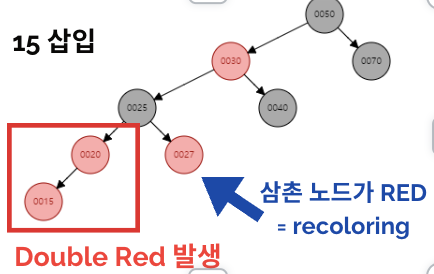
1. 새로 삽입된 노드의 부모 노드, 삼촌 노드의 색을 black으로, 조상 노드를 red로 변경

2. 조상노드가 루트이면 조상노드는 black으로 변경(루트는 black이라는 균형규칙 준수)
   

3. 조상을 red로 바꾸기 때문에 recoloring을 완료하더라도 또 double red가 발생할 수 있다. (해결될 때 까지 반복)
   

---

삭제

절차

1. 위치 찾기
2. 균형을 유지하며 삭제
3. Extra Black 처리

• 위치 찾기: 이진 탐색 트리와 같은 방법으로 삭제할 데이터가 있는 노드의 위치를 찾는다.

• 균형을 유지하며 삭제: 함부로 삭제하면 Black Depth(리프부터 루트까지의 black의 수)가 달라져 균형이 깨질수가 있기 때문에 고려하여 삭제한다.

• Extra Black 처리: 위의 과정에서 균형을 유지하기 위해 Extra Black이 사용되었다면 이를 해결한다.

삭제의 규칙

• 타겟노드, 삭제된 노드, 대체할 노드 3개를 구별해야 한다.
• 삭제된 노드가 black이면 대체할 노드에 Extra Black을 남긴다.
• Extra Black이 있다면 반드시 처리한다.

균형을 유지하며 삭제

• 타겟 노드가 자식이 1개 또는 0개일 경우
  (타겟 노드 == 삭제되는 노드)

  • 타겟 노드가 red이면 즉시 삭제 후 자식이 해당 노드 위치를 대체(자식이 없으면 대체는 없음)
    
    
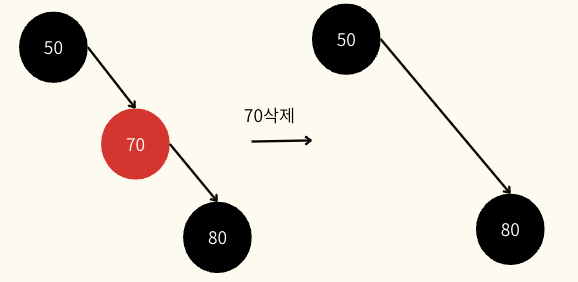
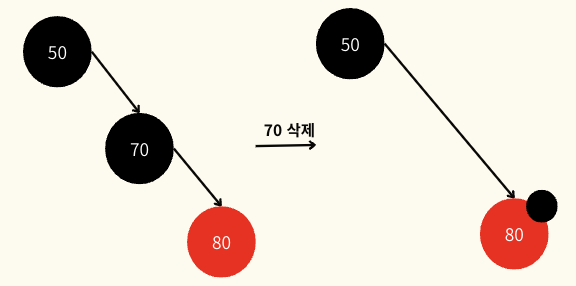
  • 타겟 노드가 black이면 삭제시 black depth가 1 줄어들고, 이를 맞춰야 하기 때문에 그 자리를 대체할 노드에 Extra Black 마크를 남긴다.
  • 자식이 없는 black을 삭제하는 경우 NIL노드를 빌려와 대체하고, Extra Black 마크를 남긴다.

  

• 타겟 노드의 자식이 2개인 경우
  (타겟노드 != 삭제되는 노드)

  • 타겟의 자식이 2개면 함부로 삭제시 균형이 깨질 가능성이 매우 높기 때문에, 이진 탐색 트리의 법칙에 맞게 값만 복사해와 대체하고 값을 빌려준 노드를 삭제한다.

  <타겟 노드: 70일 경우>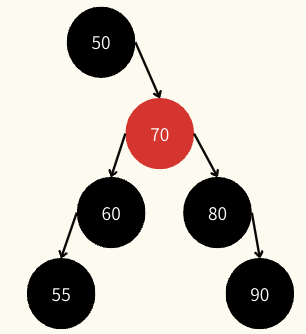왼쪽 서브트리의 최댓값 or 오른쪽 서브트리의 최솟값을 복사

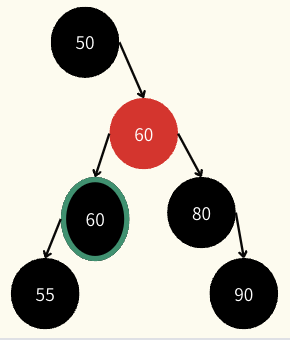  중복이 발생하면 안되기 때문에 값을 빌려준 노드(초록색표시)를 타겟대신 삭제

  이때 삭제되는 노드가 red면 black depth에 영향없기 때문에 그냥 삭제, black이면 그 자리를 대체할 노드에 Extra Black을 남겨 black depth를 유지

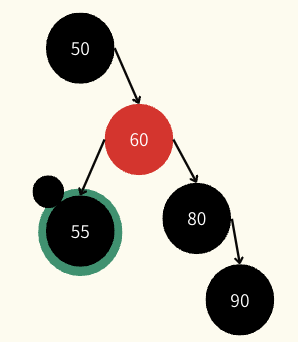
Extra Black의 처리

Extra Black은 black depth를 카운트 할때 1개로 카운트 되지만 실제 노드가 아니기 때문에 이를 없애줘야 한다.

• red - black

  red노드에 Extra Black이 붙은 상태로, red노드를 black으로 바꿔주고 Extra Black을 제거한다.
  

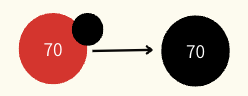
• doubly black

  black에 Extra Black이 붙은 상태로, black depth를 셀 때 2개로 세며, 이를 처리하기 위한 4가지의 경우의수가 있다.
  

doubly black의 처리

이후에 나올 4가지 CASE는 아래의 레드블랙트리의 특성을 이용하여 Extra Black을 처리하도록 정립된 방법이다.

• 하나의 black은 2개의 Extra Black으로 자식에게 나눠줄 수 있다.(단, 나눠줘도 법칙 위반이 없어야 함)

• 자식이 가진 2개의 Extra Black을 red인 부모에게 넘겨주면 Extra Black 2개가 하나로 합쳐져 이동한다.
  이후 Extra Black을 받은 부모가 red black원칙에 의해 black으로 바뀐다
  
  

CASE 1 ~ 4

위의 원리를 이용할 수 있는 상태로 red black트리의 색과 구조를 수정하는 4가지 경우의 수

핵심은 doubly black 위쪽에 red인 노드를 위치시켜 Extra Black을 올려보내 삭제시킬 수 있도록 하는 것

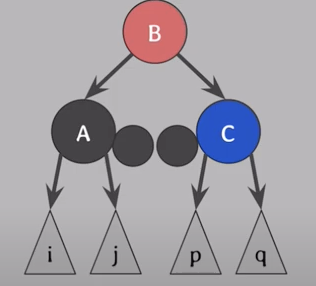
• CASE 1

  doubly black(A)의 형제가 red일 때

  doubly black(A)의 형제(D)를 black으로 만든 후 나머지 CASE중 하나로 해결
  

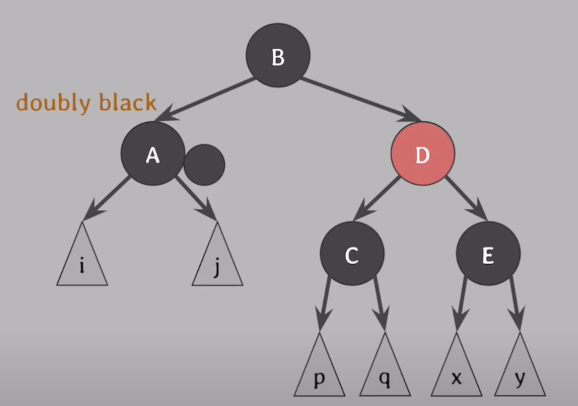
  • 해결방법

  1. 부모(B)를 기준으로 Extra Black 방향으로 회전(BST에 맞게 위치 재조정)
  2. 회전 후에도 조건 만족을 위해 부모(B)와 형제(D)의 색을 교환
  3. 아래와 같은 형태가 되면 다른 CASE들로 해결
     

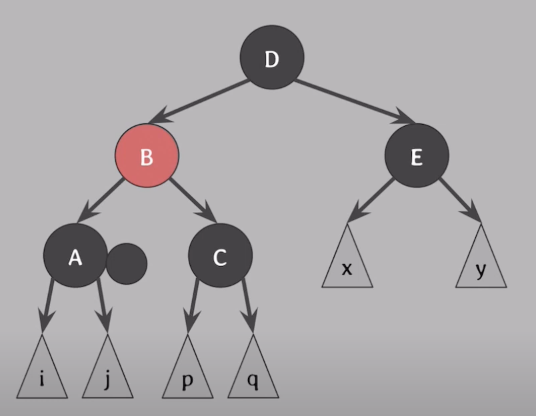
• CASE 2

  doubly black의 형제와 두 자녀 모두 black일 때
  

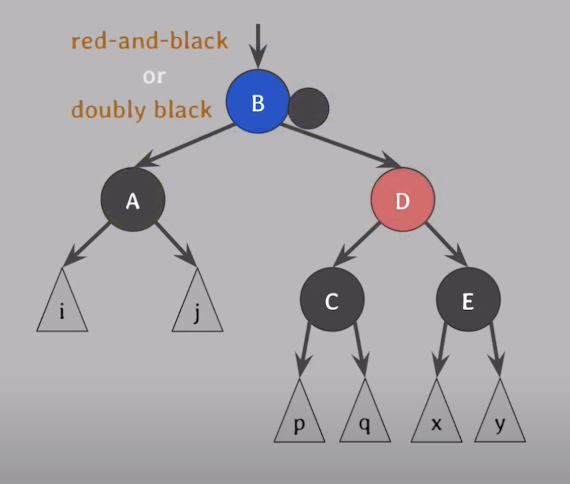
  • 해결방법

  1. doubly black(A)과 형제(D)의 black을 모아 부모(B)에게 전달
  2. 부모(B)가 red라면 black으로 바꾸고 해결, 아니라면 나머지 CASE 중 하나로 해결

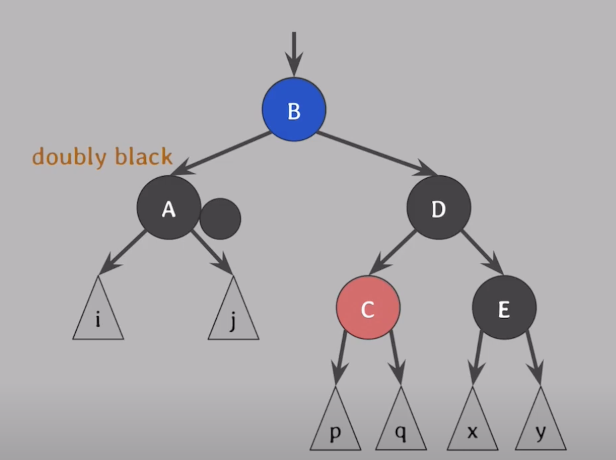
• CASE 3

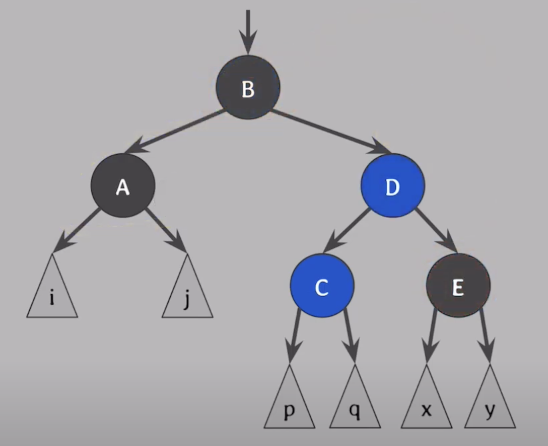
doubly black의 형제(D)가 black이고, 형제의 안쪽 자녀(C)가 red, 바깥쪽 자녀(E)는 black일 때

형제의 바깥쪽 자녀(E)를 red로 만들어 CASE4로 해결할 수 있도록 만든다

• 해결방법

1. 형제의 안쪽자녀(C)와 형제(D)의 색을 교환
2. 형제(D)를 기준으로 서브트리를 바깥방향 회전
3. CASE4의 조건을 충족하므로 CASE4로 최종 해결
   
   

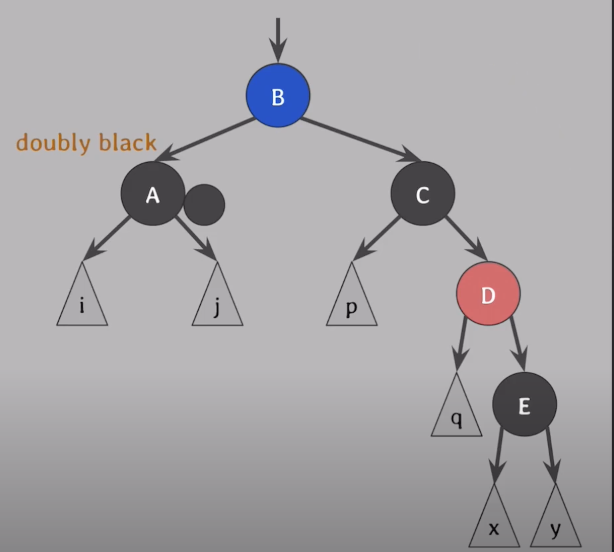
• CASE 4

  doubly black의 형제(D)가 black이고, 그 형제의 바깥쪽 자녀(E)가 red일 때(좌우측 상관없음)
  

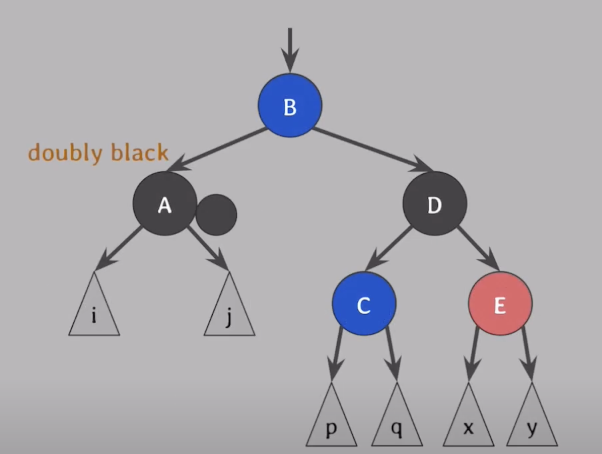
  • 해결방법

  1. 형제(D)는 부모의 색으로
  2. 형제의 바깥 자녀(E)는 black으로
  3. 부모(B)는 black으로 바꾼 후
  4. 부모를 기준으로 Extra Black이 있던 방향(A쪽)으로 회전
     

삭제 요약

• BST와 동일한 방법으로 삭제 위치를 찾음

• 단, 삭제할 노드의 색과 자녀 노드의 숫자에 따라 삭제 방법이 달라짐

• 상황에 맞는 방법에 따라 삭제할 때 Extra Black이 부여되어 doubly black 상태인 노드가 발생하면 4개의 CASE로 반드시 해결해야 함