소수 알고리즘

소수 판별 알고리즘

소수(Prime Number)란 1보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로 나누어떨어지지 않는 자연수이다.

2이상의 자연수에 대한 소수 판별 함수는 다음과 같다.

function isPrimeNumber(x) {
    for (let i = 2; i < x; i++) {
        if (x % i === 0) {
            return false;
        }
    }
    return true;
}

→ 2부터 x-1까지의 모든 자연수에 대하여 연산을 수행해야 한다. 모든 수를 하나씩 확인한다는 점에서 시간 복잡도는 O(X)이다.

약수의 성질

약수의 성질을 이용하면 시간 복잡도를 많이 줄일 수 있다.

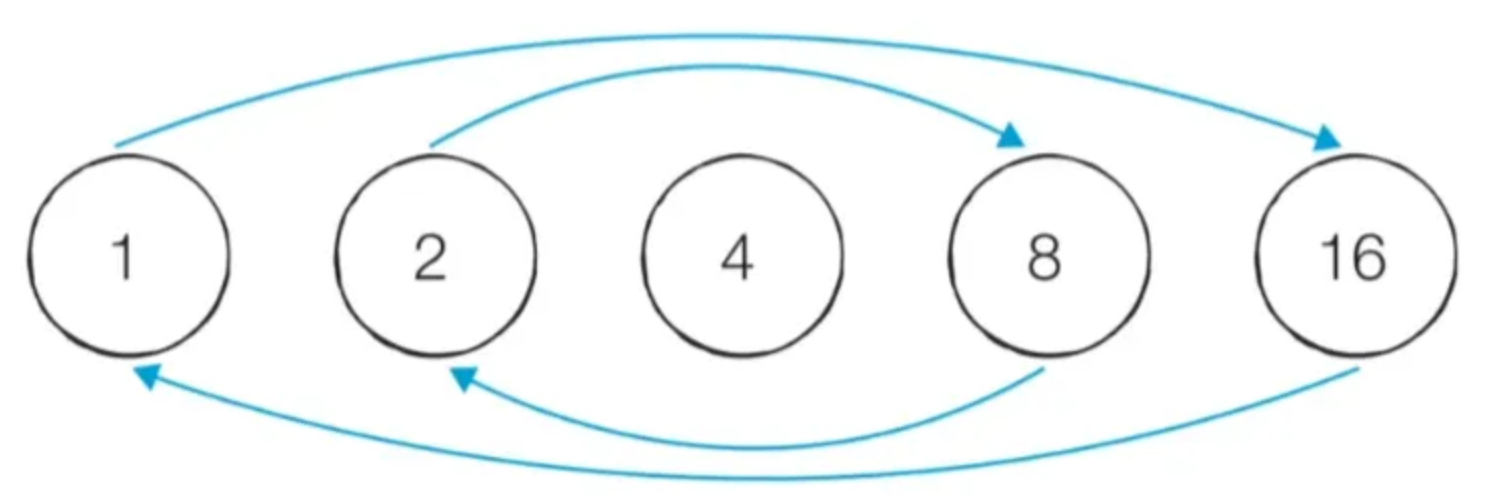
모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이룬다.

• 16의 약수는 1, 2, 4, 8, 16이다. 2X8과 8X2는 대칭이다. 따라서 우리는 특정한 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)까지만 확인하면 된다.
  

function isPrimeNumber(x) {
    if (x < 2) return false;
    for (let i = 2; i <= Math.sqrt(x); i++) {
        if (x % i === 0) {
            return false;
        }
    }
    return true;
}

→ 2부터 x의 제곱근(소수점 이하 무시)까지의 모든 자연수에 대하여 연산을 수행해야 한다. 시간 복잡도는 시간복잡도는 O(N*1/2)

다수의 소수 판별

하나의 수에 대해서 소수인지 아닌지 판별하는 방법을 알아보았다.

하지만 특정한 수의 범위 안에 존재하는 모든 소수를 찾아야 할 때는 어떻게 할까??

에라토스테네스의 체 알고리즘을 사용하자!! 😎

에라토스테네스의 체 알고리즘

다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적인 알고리즘이다.

2부터 1,000까지의 모든 수에 대하여 소수를 판별하는 코드이다.

for (let i = 2; i <= Math.sqrt(n); i++) { // 2부터 n의 제곱근까지의 모든 수를 확인하며
    if (array[i] === true) { // i가 소수인 경우 (남은 수인 경우)
        // i를 제외한 i의 모든 배수를 지우기
        let j = 2;
        while (i * j <= n) {
            array[i * j] = false;
            j += 1;
        }
    }
}

(이코테 2021 강의 몰아보기) 9. 코딩 테스트에서 자주 출제되는 기타 알고리즘