해당 문제를 확인하시고 싶으면 아래 링크를 통해 확인해주세요!
https://school.programmers.co.kr/learn/courses/30/lessons/42839
문제설명

내가 생각한 로직
- 이 문제는 순열과 조합이 필요한 문제라고 생각되어서
itertools라이브러리 적용 - 01과 1은 중복이기 때문에
set을 사용해서 중복을 없애줌 - 결과 리스트에서 각 원소가 소수인지 아닌지 확인하는 함수를 만들어서 True인 Value만 count
내 풀이
from itertools import permutations
# 소수 판별 함수
def isPrime(num):
if num <= 1:
return False
for n in range(2, num):
if num % n == 0:
return False
return True
def solution(numbers):
pset = set()
answer = 0
for i in range(1, len(numbers)+1):
perm = permutations(numbers, i) # 순열 생성
for p in perm:
pdata = "".join(map(str, p)) # 순열 데이터들
pset.add(pdata)
pset = set(map(int, pset)) # 중복제거
for num in pset:
if isPrime(num) == True: # 소수면 1 추가
answer += 1
return answer그러면 왜 블로그 정리했어?
다른 사람들의 풀이를 봤는데 정말 다양한거 같다.
그 중에서는 뭐.. 에라토스테네스의 체를 사용하신 분도 계셨고, permutation 라이브러리를 사용하지 않고 재귀로 구현한 개발자분도 계셨다.
그래서 이번 블로그에서는 에라토스테네스의 체에 대해서 알아보고 permutation을 재귀적으로 구현한 코드도 분석해보려고 한다.
(1) 에라토스테네스의 체
에라토스테네스의 체는 고대 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법이다.
체로 치듯이 수를 걸러낸다는 뜻을 가지고 있기도 하다.
먼저 간단하게 말씀드리면 1과 2,3,5,7의 배수인 수들을 모두 제거하면 소수만 남는다는 것이다.
소수는 1과 자기자신을 제외한 약수를 가지는 합성수이다. 즉 1과 자기자신 이외에 약수를 가지게 되는 경우를 제거해야 소수가 되기 때문에
1을 예외로 제거하고 2,3,5,7의 배수를 제거하면 결국 남는건 소수뿐이라는 것이다.
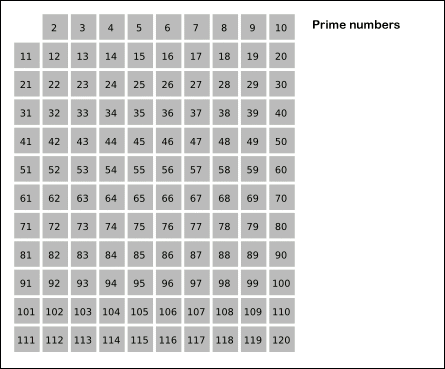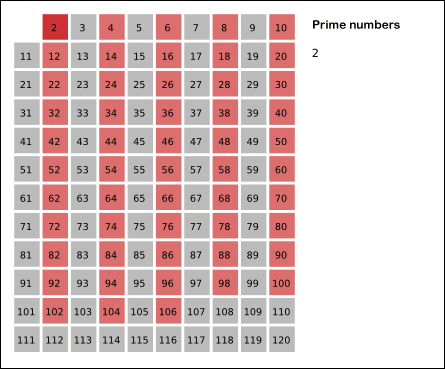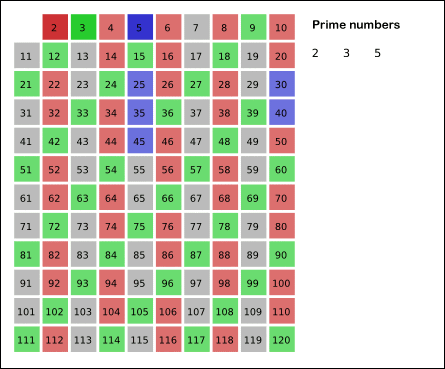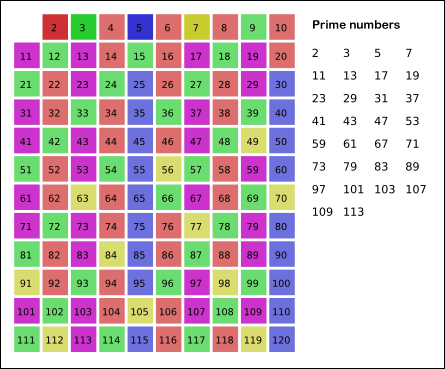
그림의 경우, 11^2(121) >120 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2,3,5,7의 배수를 지우고 남는 수는 모두 소수다.
그래서 이 알고리즘은 어떻게 진행되는데?
그림이랑 함께 봅시다!
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. (회색 사각형)
- 2는 소수이니까 오른쪽에 2를 쓴다.
- 자기자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수에서 3도 소수이니까 오른쪽에 3을 쓰고 자기자신을 제외한 3의 배수를 모두 지운다.
- 위의 로직들을 5,7에도 똑같이 적용한다.
- 최종적으로는 구간의 모든 소수들이 남게 된다.
Code
def prime_list(n):
check = [True] * n
m = int(n ** 0.5)
for i in range(2, m+1):
if check[i] == True:
for j in range(2*i, n, i):
check[j] = False
return [i for i in range(2, n) if check[i] == True]첫 번째 중요한점
m = int(n ** 0.5)
for i in range(2, m+1):예를 들어 변수 m 사용없이 for문을 (2, n+1)로 돌아간다면 2~10까지의 배수를 False로 바꾸게 될텐데 이 부분은 변수 m을 사용하게 되면 바로 해소되는 부분이기 때문에 반복적인 부분을 낭비하는 것이 된다.
따라서, 나열된 수를 제거하는 최대의 배수는 무조건 n의 제곱근 이하이므로 제거할 합성수를 for i in range(2, m+1)로 i를 제한시킨다. 이때 최소한 2의 배수부터 제거를 해야하기 때문에 range가 2부터 시작한다.
두 번째 중요한점
for i in range(2, m+1):
if check[i] == True:
for j in range(2*i, n, i):
check[j] = False나열된 수의 위치(i)가 True이면 2i부터 n까지 i만큼 커지면서 check[j] 자리의 값을 False로 설정해주는 것이다. 다시 말해서 자기 자신(2,3,5,7)은 남겨둬야 하기 때문에 range를 (2i, n, i)로 설정하면서 소수가 아닌 수를 제거해 나가는 것이다.
세 번째 중요한점
하지만 이 문제처럼 소수 확인할 수가 몇개 안되는 경우에는 오히려 에라토스테네스의 체를 사용하는거 보다 완전탐색으로 각각 소수인지 판단하는게 오히려 효율적일수도 있다. 이점은 참고하자!
(2) 재귀함수로 구현하는 permutation
number_set = set()
def permutation(base, array):
if base:
number_set.add(int(base))
for i, s in enumerate(array):
permutation(base + s, array[:i] + array[i+1:])
permutation("", list("17"))혹시나 해서 가져와봤다. 참고로 알아두기만 하자!
