탐색트리I

자료구조란

• 내가 어떤 하고싶은 것이 있을 때 효율적으로 처리해주는 것

#집합을 표현하는 자료구조

• 수학의 '집합'개념 이용

집합에 대한 연산

• membership query
  - 어떤 원소가 집합의 원소인지 판단하는것
• insertion
  - 생성자
• deletion
  - 빼다가 전부빼면 공집합, 소멸자

배열

• O(N)MEMBERSHIP QUERY, O(1) insertion, O(n)deletion
• 더 빨리할 수 있는법이 있을까?, 더 메모리를 낭비하지 않는 방법은?

탐색트리

레코드

• 개체에 대한 모든 정보를 묶은 저장 단위
• ex) 주민등록번호, 이름, 주소, 전화번호 ..

키

• 각 레코드를 대표할 수 있는 값
• 대표란 1대1대응이 되는것을 의미, 이름같은경우 동일이름 가능하여 대표 불가능, 학번은 가능

탐색트리

• 각 노드마다 하나의 키를 가지는 트리
• 해당 레코드가 저장된 위치를 찾을 수 있다.

이진탐색트리

• 각노드가 최대 두개의 자식을 같는 탐색 트리
• 왼쪽 자식은 부모보다 키 값이 작고, 오른쪽 자식은 부모보다 키 값이 크다.
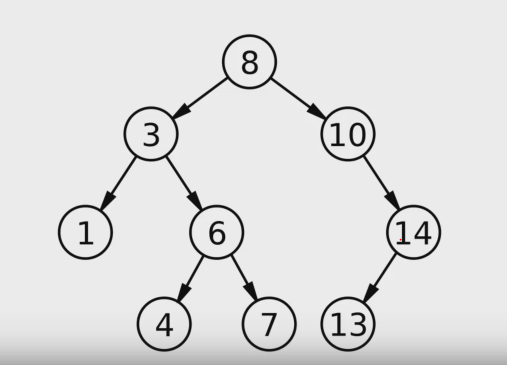
• ex)
  
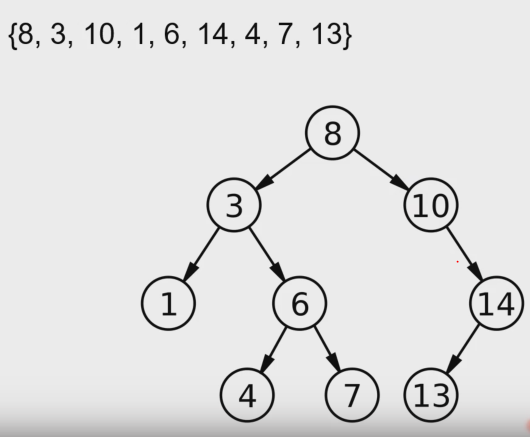
  서브트리
• 특정 노드와 그 이하의 노드로만 이루어진 트리
  
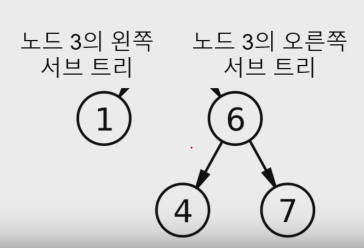
• 이진 탐색트리는 유일하지않음
• 만약 어떤 키 값이 자주 접근될 지 모른다면, 균형잡힌 트리가 유리
• 만약 1값이 가장 자주 접근된다면 균형이 잡히지 않은 것이 유리함

이진탐색트리에서 검색

1. 이진 탐색 트리에서 원하는 값 k가 들어있는지 확인하는 법

2. 재귀적인 구현

• 트리가 비어 있다면 k는 트리에 있을 수 없다.
• 만약 루트의 값이 k라면 리턴
• 만약 루트값이 k보다 크다면 이 값은 루트의 왼쪽 서브트리에 존재
• 만약 루트값이 k보다 작다면 이 값은 오른쪽 서브트리에 존재
• 반복

이진트리에서 삭제I

1. 삽입에 비해서 삭제는 상대적으로 어렵다
2. 이진탐색트리에서 한키를 삽입하면 확실히 그 결과가 이진 탐색트리이다.
3. 이진 탐색트리에서 한 노드를 삭제하면 그 결과가 이진트리가 아닐수도 있다. 루트를 삭제할 경우 트리가 이분할 될 수 있다.

이진탐색트리 가장 간단한 삭제

1. 이진탐색트리 순회하면서 저장된 모든 값을 하나씩 읽는다.
2. 읽은 값이 삭제할 값이 아니라면, 새로운 이진 탐색트리에 하나씩 삽입한다.
3. 읽은 값이 삭제할 값이라면 건너뛴다.
4. 시간복잡도, 공간복잡도는 O(n)
5. 일을 많이하여 효율적인 방법은 아니다.

이진탐색트리에서 삭제II

1. 삭제할 노드가 무엇인가에 따라 세가지 경우 존재한다.

• 삭제할 노드가 리프
  - 단순히 지우면 된다.
• 삭제할 노드가 자식하나
  - 노드를 지우고, 자식을 원래 노드의 위치를 옮긴다.
• 삭제할 노드가 자식 둘
  - 방법1: 서브트리의 원소들을 모두 모아 다시 트리를 만든다.
  -방법2: 트리의 모양을 최대한 유지한다.
  -노드의 키 값보다 바로 앞에 있거나, 바로 뒤에 있는 노드를 찾는다.
  -이 노드가 원래 노드의 위치로 오고, 다시 이 노드를 지우는 과정을 반복한다.
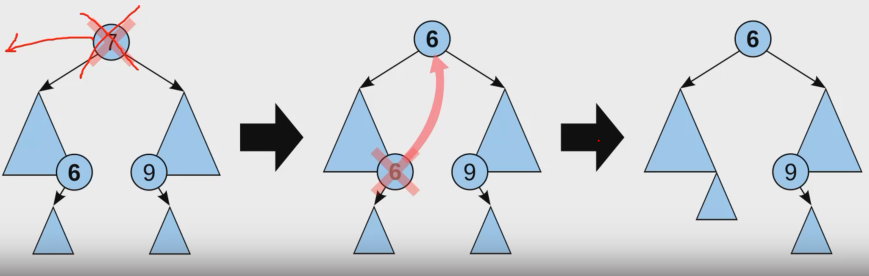
  • O(h) 시간( 트리의 높이 만큼)
    
• 루트7을 삭제한 경우
  - 바로 앞 값 6을 올린다.
  -바로 앞 값은 왼쪽 자식의 가장 오른쪽 자손, 또는 오른쪽 자식의 가장 왼쪽 자손임
  -6이 지워지면서, 유일한 자식이 6의 자리로 이동, 6의 오른쪽 자식은 있을 수 없다.

레드 블랙 트리

1. 이진 탐색 트리의 경우 한 쪽으로 노드들이 쏠릴 수 있다.

• 트리의 삭제 삽입,검색연산은 모두 트리의 높이 h에 비례하는 시간이 걸린다.
• h = O(log n)만족 가능한가?

2. 레드 블랙 트리

• 이진탐색트리에 추가적인 성질이 추가된 트리
• 각 노드는 RED 또는 BLACK 둘 중 한가지 색이 칠해짐
• 루트는 BLACK
• 노드의 색이 RED이면 자식이 색이 RED일 수 없다.
• 루트부터 어떤 리프로든 모든 경로에서 만나는 BLACK 노드의 수는 항상 일정하다.

레드 블랙 트리에서 삽입

1. 이진 탐색 트리에서 삽입과 동일, 색깔때문에 추가 절차 들어간다.
2. 새로 삽입된 노드는 RED

• Black height를 맞추는데 유리하다.

3. 두가지 경우에 대해 색깔이 다음과 같이 조정된다.

• 새로 삽입된 노드의 부모 색이 RED라면, 한쪽에 연속으로 삽입된 경우
• BLACK부모 밑에 계속 삽입이 되었다면 두 자식이 모두 RED인 경우는 가능하다.
• CASE 1 : 한 RED인 자식 밑에 RED가 삽입된 경우
• CASE 2 : BLACK인 부모 밑에 두 RED인 자식이 있고, 이 자식에 다시 RED가 삽입
• CASE1 : 4가지 경우가 존재한다.
  
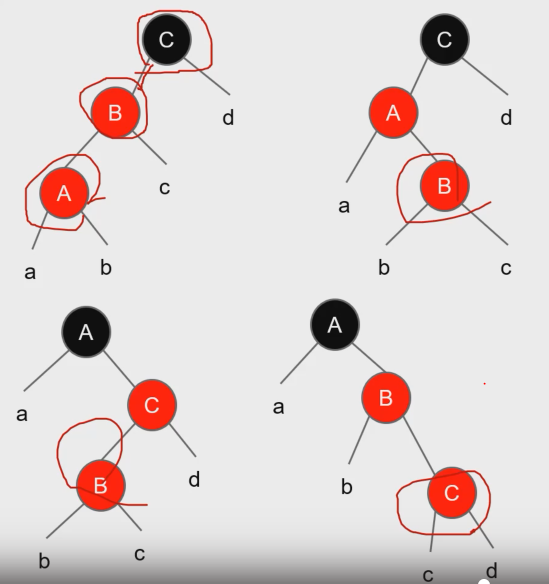
  -> 모두 A(RED) - B(BLACK) - C(RED)형태의 트리로 해결 가능하다.
• 언제나 상수배만큼의 작업을 해서 트리를 재변경한다.

시간분석

1. 루트에서 리프까지 거리는 가장 긴 경우에도 가장 짧은 경우의 두배 이내

• 가장 짧은 경우는 모두 BLACK NODE인 경우, 가장 긴 경우는 BLACK-RED-BLACK 번갈아 있을 경우

2. Black height를 bh라고 하면 다음 식이 성립.

• 트리의 노드의 개수를 n이라고 하면
• n>= 2^bh-1(모든 노드가 black node)
• n<=4^bh-1(black-red-black번갈아 있을 경우)
• 두식을 풀면 1/2log(n+1)<=bh<=log(n+1)
• 트리의 높이 h는 bh<=h<=2bh이므로 삽입, 탐색 모두 최대 2log(n+1)시간 이내에 수행 가능하다.