[신입생 세미나] Lecture 3: Linear Classifiers [DL for CV]

본 게시물은 고려대학교 스마트생산시스템 연구실 2023년 동계 신입생 세미나 활동입니다.
Michigan 대학의 Justin Johnson 교수님의 강의를 공부하는 형식입니다.
관련 유튜브 영상은 여기에서 확인 가능합니다.

---

Lecture 3: Linear Classifiers 강의에서는 배울 수 있는 내용은 다음과 같습니다.
- Linear Classifiers 정의
- Linear Classifiers 바라보는 여러 관점들
- Loss Function 정의
- Regularization
- Cross-Entropy Loss & SVM Loss

---

Linear Classifiers 정의

Linear Classifiers (선형 분류기) 는 Neural Network 의 근본입니다.

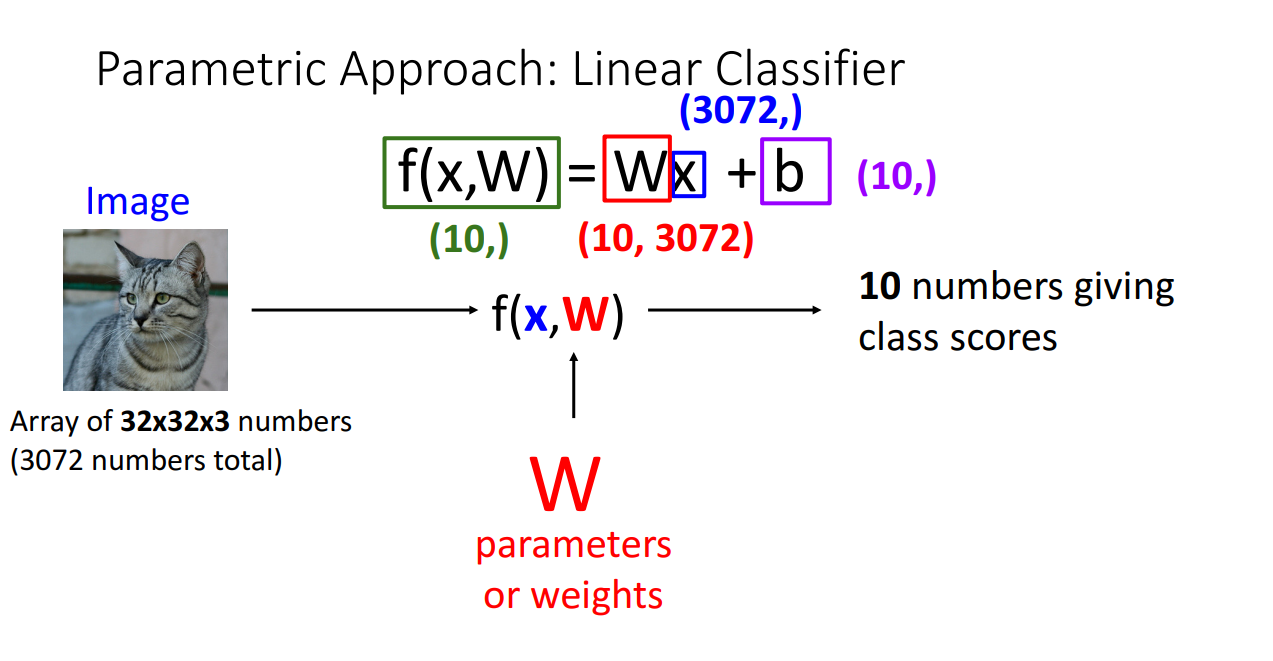
교수님은 먼저 Linear Classifiers를 설명하기 위해 Parametric한 방법을 제시합니다.

위 그림을 보시면 알 수 있듯이, 원본 이미지의 spatial structure를 무시하고 늘린 다음에 Weight 행렬과 곱해준 후 Bias 벡터를 더해줍니다.

이 때 Weight 행렬의 차원은 전체 클래스의 수 X 원본 이미지의 차원 입니다.

해당 행렬곱을 통해 입력된 이미지가 어느 클래스의 해당하는지 판단하기 위한 지표를 산출해내게 됩니다.

---

Linear Classifiers 바라보는 여러 관점들

위에서 정의된 Linear Classifiers를 교수님께서는
각각 Algebraic Viewpoint, Visual Viewpoint, Geometric Viewpoint로 설명 및 해석합니다.

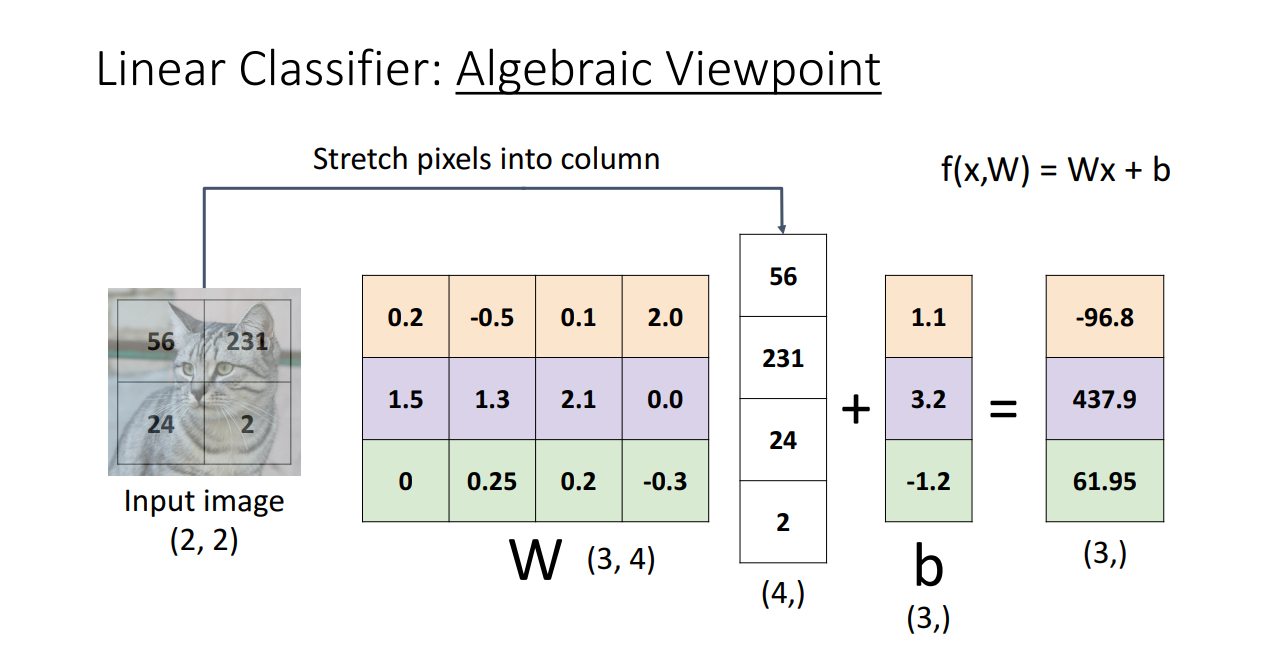
첫 번째로, Algebraic Viewpoint (대수적 관점) 입니다.

이는 앞서 제시한 Linear Classifiers를 행렬곱을 사용해서 계산한 결과입니다.

이와 같이 표현해도 되지만 교수님께서는 아래와 같이 bias 벡터 또한 Weight 행렬에 포함시켜서
한 번의 행렬곱으로 결과를 산출할 수 있다고 합니다.

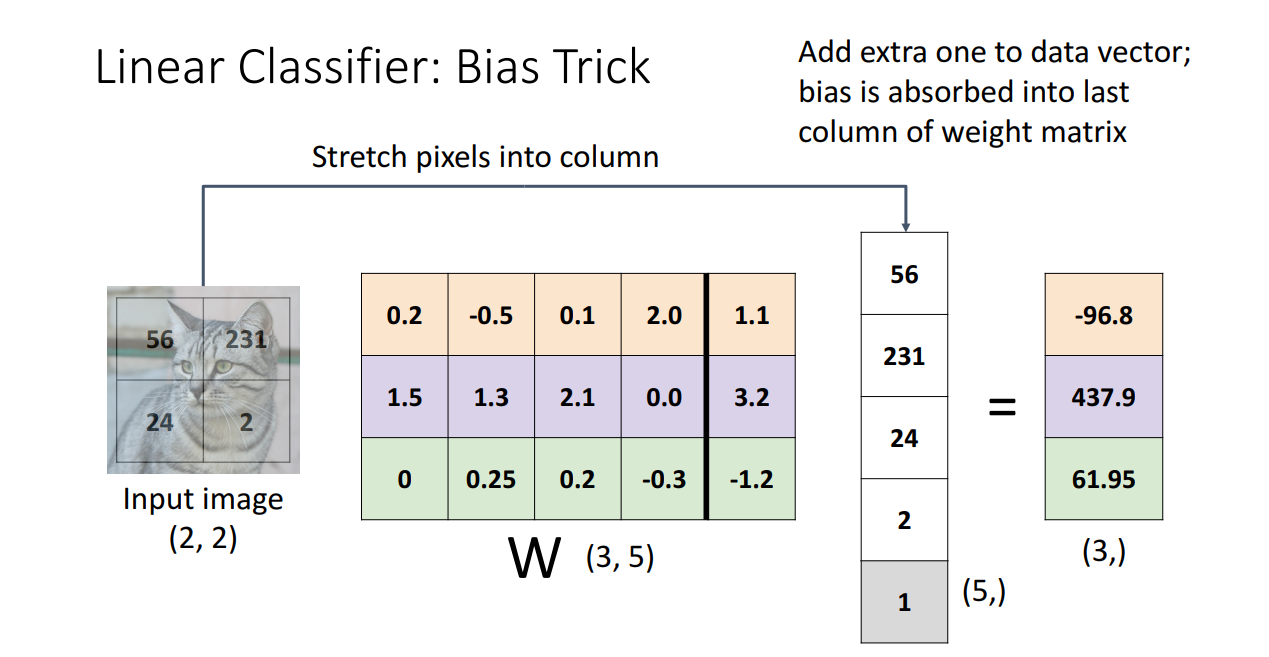
Bias Trick은 Algebraic Viewpoint에서 Lienar Classifiers를 이해하는 데에는
분명히 도움이 되지만 Convolutional, Regularization, Initialization을 수행할 때는 다시 분리해서 해야하기 때문에 부적합하다고 합니다.

대수적 관점에서 봤을 때, Linear Classifier의 특징 중 하나는 Predictions (예측값) 또한 Linear하다는 점입니다.

위 그림을 보시면 Image를 입력으로 넣었을 때 3개의 클래스에 해당하는 Score 값이 나와있습니다.
이 때 원본 이미지에 0.5를 곱해서 흐리게 만들지라도 Score도 그대로 0.5가 곱해져서 분류 Task를
수행하는 데에는 크게 문제가 없어보입니다.

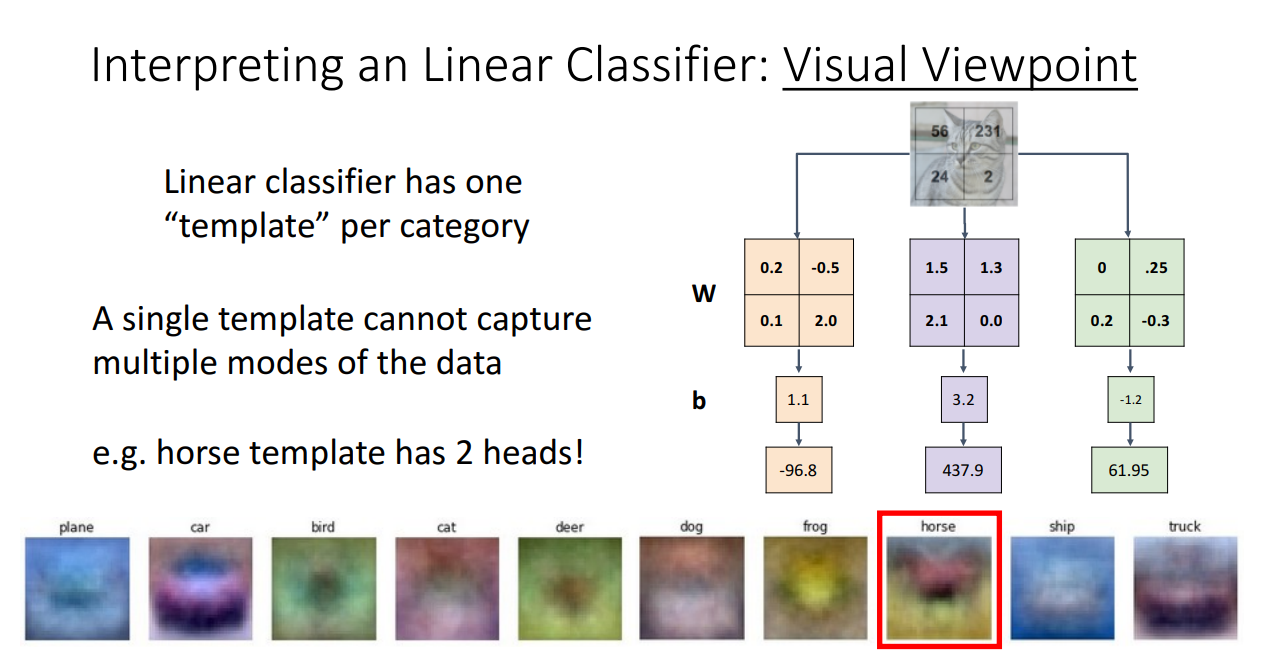
두 번째로, Visual Viewpoint (시각적 관점) 입니다.

이를 위해서 무너뜨렸던 Spatial Structure를 다시 이미지 형태로 복원해서 설명합니다.

해당 방식으로 접근하면 context cue를 알아보기 쉽습니다.

그리고 각 category별로 weight는 "Template"으로 이해하면 되고,
이는 이미지 어디에 더 중점을 둬서 scoring 하는지에 대한 정보가 됩니다.

Template 으로 weight을 바라본다면 Linear Classifier의 단점을 찾아낼 수 있습니다.

A single template cannot capture multiple modes of the data
가 단점이고 예를 들어 빨간 차만 학습했다면, 파란 차, 초록 차는 분류 못하는 상황입니다.
또 하나의 예시로 말이 왼쪽, 오른쪽 어느 방향을 보는지 하나밖에 학습을 못하기 때문에
위 상황에서 둘 다를 만족시키기 위해 말의 머리가 2개로 잘못 산출되는 상황이 생깁니다.

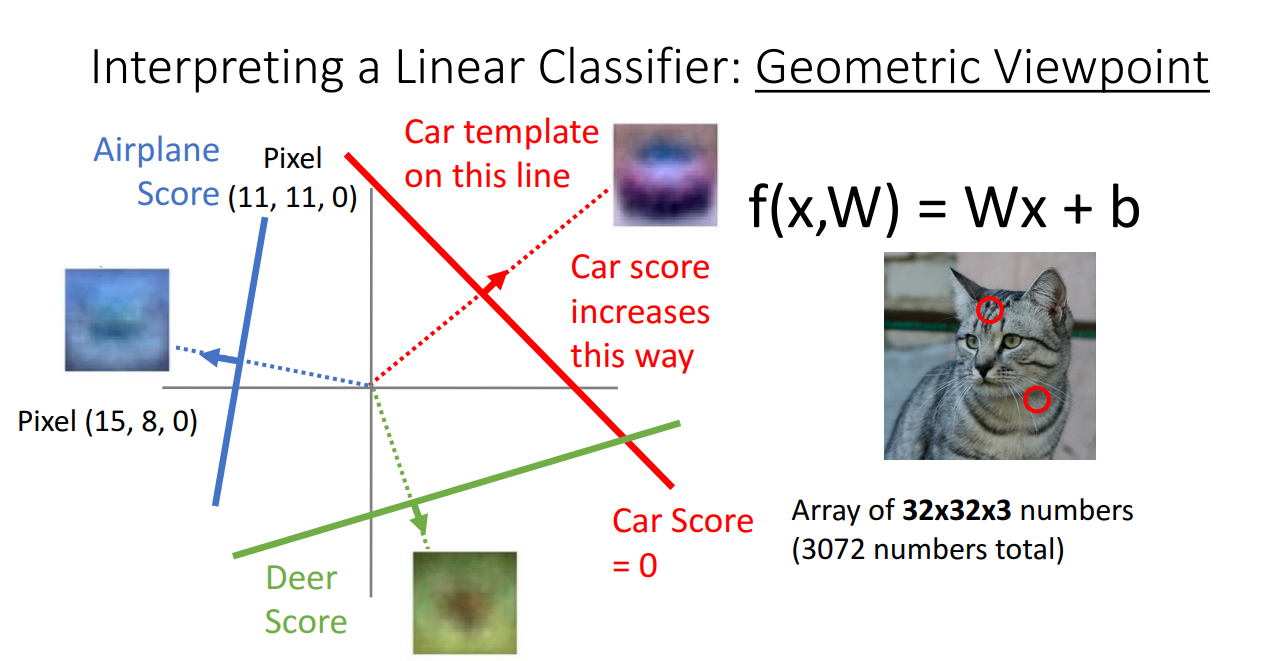
세 번째는 Geometric Viewpoint (기하학적 관점) 입니다.

위 그림의 상황은 이미지의 특정 두 point를 가지고 2차원 공간에서 데이터들을 타점한 상황입니다.

2차원 공간에 타점했을 때 class 별로 다른 형상을 띔을 알 수 있고 이를 구분해주는 Linear Classifier를 그려줄 수 있습니다.

예시 상황은 비록 두 point의 픽셀을 타점했지만 더욱 고차원이 된다면 Linear Classifier가 단순한 직선을 넘은 Hyperplane이 될 것입니다.

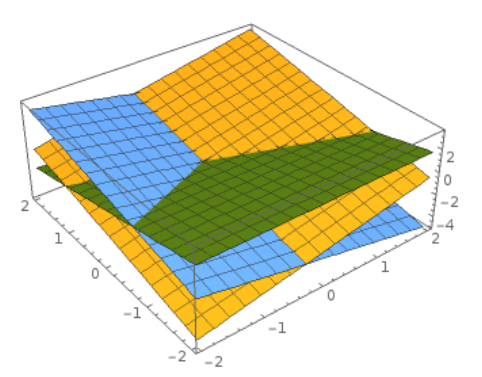
3차원에서 표현해준 모습은 다음과 같습니다.

인간은 저차원으로밖에 이해할 수 없기에 고차원의 개념을 저차원으로 이해하려는 시도는 intuitive 합니다.

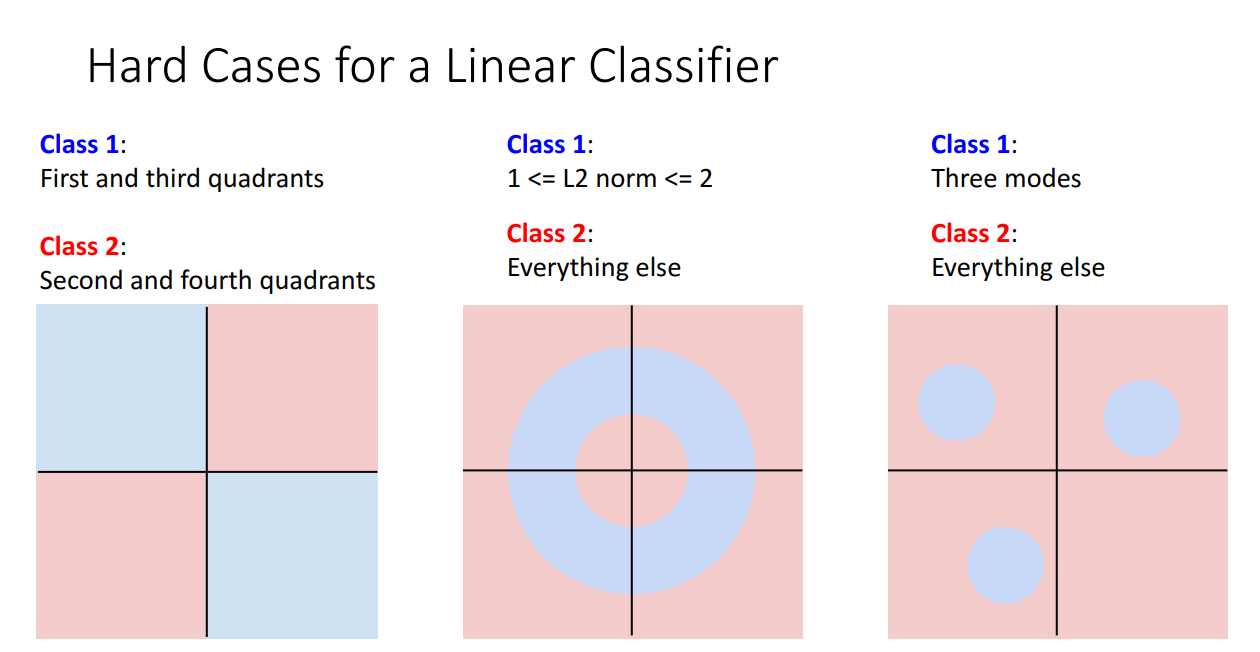
Linear Classifier로 해결하기 힘든 문제들도 분명 존재합니다.

위 예시의 경우가 그렇습니다. Disjoint한 region이 각 class로서 존재한다면 선형 분류기를 사용하여 분류하는 것에 분명 한계가 있습니다.

퍼셉트론을 공부할 때 나오는 XOR 문제가 대표적입니다.

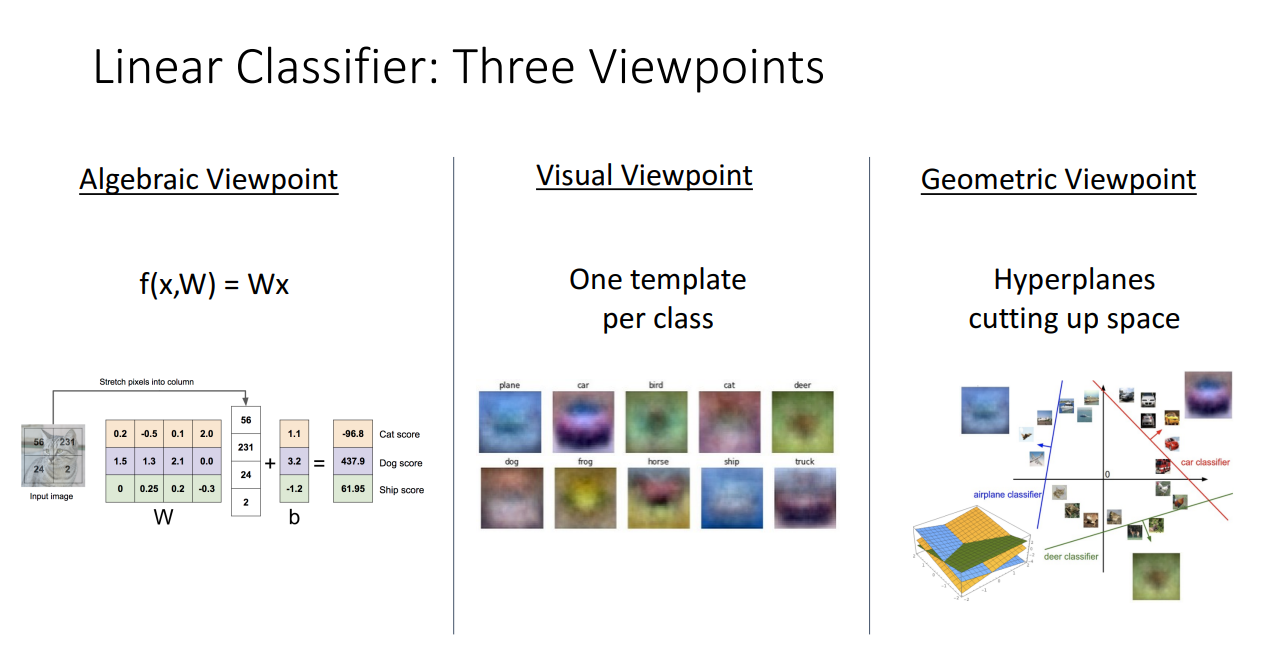
정리하자면 Linear Classifier를 바라보는 관점은 위 그림처럼 나눌 수 있고
각각의 관점은 Linear Classifier의 작동 원리를 이해하는 데에 모두 도움이 됩니다.

---

Loss Function 정의

지금까지 Linear Classifier가 무엇이고 어떻게 작동하는지 여러 관점에서 살펴보았습니다.

이를 통해 Linear Classifier는 각 Class를 잘 나누도록 Weight을 설정하여 input에 곱해진다는 것을 알 수 있었습니다.

그렇다면 여기서 생기는 의문은 이것입니다. 어떤게 좋은 Weight일까?

좋은 Weight을 선택하기 위해서 두가지 과정을 거칩니다.

1. Weight 값이 얼마나 좋은지 정량화하는 Loss Function
2. Loss Function을 최소화할 수 있는 Weight 찾기 (Optimization)

여기서 Loss Function은 Objective Function / Cost Function으로도 불리고,
모델을 평가할 수 있는 정량적 방법입니다.

위 그림과 같이 loss function 값이 낮으면 좋은 분류기 / 높으면 나쁜 분류기입니다.

$f(x_i,W)$는 Prediction, $y_i$는 ground truth 입니다.

전체 Dataset의 Loss는 각 샘플별 loss의 평균입니다.

여러 Loss Function 중 첫번째로 설명된 Loss Function은 Multiclass SVM Loss 입니다.

해당 손실함수의 아이디어는 정답 class의 score는 다른 score에 비해 높아야한다 입니다.

위 그래프를 보면 x축이 Score, y축이 Loss 입니다.

정답 대신 다른 class로 예측했을 때의 Loss는 높고, Score는 낮습니다.
정답에 가깝게 예측할 수록 Loss는 linearly decrease하고, 정답 class로 예측하면 Loss는 0입니다.

이에 따라 수식을 작성하면 $L_i = \sum_{j\ne y_i} max(0, s_j-s_{y_i}+1)$ 이고,
이는 correct class를 exclude한 상황입니다.

아래 예시를 보면 이해가 쉽습니다.

해당 Loss에 대해서 교수님은 여러 질문을 던집니다.
한 번씩 생각해보시면 좋은 질문들입니다.

Q. score 값이 살짝 변화하면 Loss에 영향을 주는가?
A. 한 번 옳게 예측하면 score가 살짝 변한다고 해서 loss에 영향을 주지 않는다.

Q. Loss의 min과 max는?
A. 0과 $\infin$ , 무한대인 경우는 correct category score 값이 굉장히 작을 때이다.

Q. Score를 Randomly initialize 한다면?
A. Loss 값 또한 small random 값.

Q. 만약 correct class도 Loss sum 계산에 들어간다면?
A. 모든 Loss가 1씩 증가 --> 순서에 영향은 없기에 결과는 안 달라진다.

Q. Loss에 sum 대신 mean 쓰면?
A. monotonic transform일 뿐 결과에 큰 변화는 없다.

Q. $L_i = \sum_{j \ne y_i} max(0, s_j - s_{y_i} + 1)^2$를 대신 쓴다면?
A. 더 이상 Multi-class SVM Loss 라고 할 수 없다.

Q. $L=0$ 이 되는 W를 찾았다면 W는 unique한가?
A. 아니다. 2W 또한 $L=0$이 되게한다.

마지막 질문에 대한 대답을 들으면 하나의 고민이 또 생깁니다.

둘 다 Loss 값을 0으로 잘 산출했는데 그럼 어떤 Weight을 선택해야할까?
이 경우에 교수님은 Additional mechanism Regularization이 필요하다고 합니다.

---

Regularization

Regularization은 data에 depend 하지 않습니다.
오히려 모델이 너무 training data에 집중하는 것을 방지합니다.

위 그림에서 $\lambda$는 어느 정도로 규제할지 결정하는 지표로 hyperparameter입니다.

예시로 나온 Regularization은

• Simple Ex : L2, L1, Elastic net (L1 + L2)
• Complex Ex : Dropout, Batch normalization, Cutout, Mixup, ...

해당 Regularization에 대한 구체적인 설명은 없었지만 아마 강의가 진행되면서 나올 것 같습니다.

Regularization을 사용하는 목적은 다음과 같습니다.

• Express preference
• Avoid Overfitting --> Optimization과 다른 지점 / for unseen data
• Improve optimization

첫 번째 목적에 대한 이해를 돕기 위해 아래 그림을 가져왔습니다.

두 weight 모두 input x와 곱해지면 1을 산출합니다.
해당 상황에서 L2 Regularization을 더하면 $w_2$를 곱한 경우가 더 낮은 Loss를 산출하게 됩니다.

즉, L2 Regularization은 weight을 하나의 feature에 몰아주는 것보다 spread out 하는 것을 선호합니다.

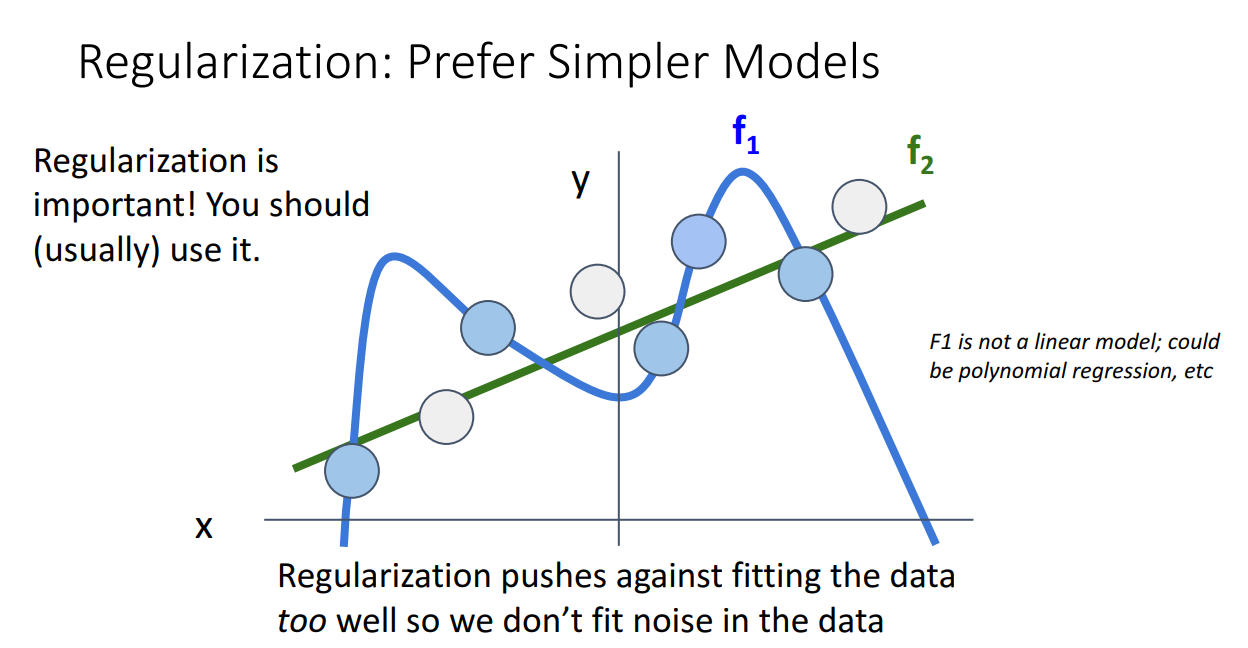
위와 같은 두개의 모델이 있다고 했을 때 Regularization은 $f_1$에 더 큰 규제를 가합니다.
이는 너무 data에 overfit 하는 것은 Regularization이 선호하는 방향이 아니라는 걸 뜻합니다.

이와 같이 교수님은 Loss Function을 잘 고르는 것도 중요하지만 Regularization을 함께 잘 쓰는 것의 중요성도 강조합니다.

---

Cross-Entropy Loss & SVM Loss

다음으로 앞서 본 SVM Loss 외에도 Cross-Entropy Loss가 소개됩니다.

해당 Loss Function을 사용한 이유는 classifier score를 확률적으로 살펴보기 위함입니다.

그 동안 예시로 나왔던 score는 위 파란 박스처럼 그냥 숫자였습니다.
여기에 exponential (지수) 함수를 취해서 빨간 박스처럼 0보다 큰 숫자로 만듭니다.
그 다음 normalize 시켜서 초록 박스처럼 확률로 나타냅니다.

이렇게 확률로 나타내면 0 또는 1로 class를 구분하지 않기 때문에,
Diffrentiable (미분 가능한) 합니다.

그런 다음 Correct Probability와 KL Divergence로 차이를 구하여 Cross-Entropy Loss로서 사용합니다.

앞서 SVM Loss 에서 했던 질문들을 Cross-Entropy Loss에서도 합니다.

Q. Cross-Entropy Loss의 min/max?
A. min, max는 동일하게 0, $\infin$ 이지만, min은 0이 되는 경우가 극히 드물다.

Q. 모든 score가 small random value라면 loss는?
A. $-log(1/C) = log(C)$, 해당 값은 Benchmark가 될 수 있는데 해당 값보다 Loss가 크다면 Worse than Random 상황이기 때문이다.

Q. score 값이 살짝 변화한다면?
A. SVM Loss는 동일 / Cross-Entropy Loss는 변한다.

Q. correct class의 score가 두배가 된다면?
A. SVM Loss는 여전히 동일 / Cross-Entropy Loss는 감소.