데이터베이스 정규화

박기범·2021년 12월 19일

~~인덱스, 트랜잭션, 트랜잭션 고립 수준에 이은 정규화이다. 이럴 줄 알았으면 그냥 데이터베이스 시리즈를 묶을걸 그랬다.~~

~~백앤드 개발자를 희망하기에 DB를 열심히 공부하면서 느끼는 점은, 기업이 돈을 주고 DBA를 고용하는데는 다 이유가 있다는 것이다. 젠장!~~

?? 다 들었다고?? 무엇을 들었다는 말인가?
필자는 아무말도 하지 않았다. DB공부하는게 너무나 즐거워서 잡담을 할 시간조차 없는걸!

정규화에 대해 시작하자. 지저분한 나의 릴레이션을 깔끔하게 나눠볼 시간이다.

정규화 개요

그런데 왜 릴레이션을 깔끔하게 나누어야 할까? 항상 방이 더러우면 할 일에 제대로 집중을 못하니 내 방을 치우라는 부모님의 잔소리를 들을 때마다 '나는 편한데 왜 그러시지..' 라는 생각을 했다. 놀랍게도, 부모님의 잔소리에도, 정규화를 하는데에도 다 이유가 있다. ~~어른들의 말씀은 틀린것이 없다.~~

정규화는 데이터의 중복과 갱신 이상을 막아 효율적인 데이터베이스를 설계하기 위해 진행한다. 그렇다면 역시, 갱신 이상이 무엇인지 알아야겠다.

갱신 이상

데이터의 갱신 이상이란, 다음과 같은 경우를 뜻한다.

수정 이상
반복되는 데이터의 일부만 수정하면 데이터의 불일치가 발생한다.
삽입 이상
불필요한 정보를 함께 저장하지 않고는 특정 정보를 저장할 수 없다.
삭제 이상
유용한 정보를 함께 삭제하지 않고는, 특정 데이터를 삭제할 수 없다.

다음 릴레이션을 보자.

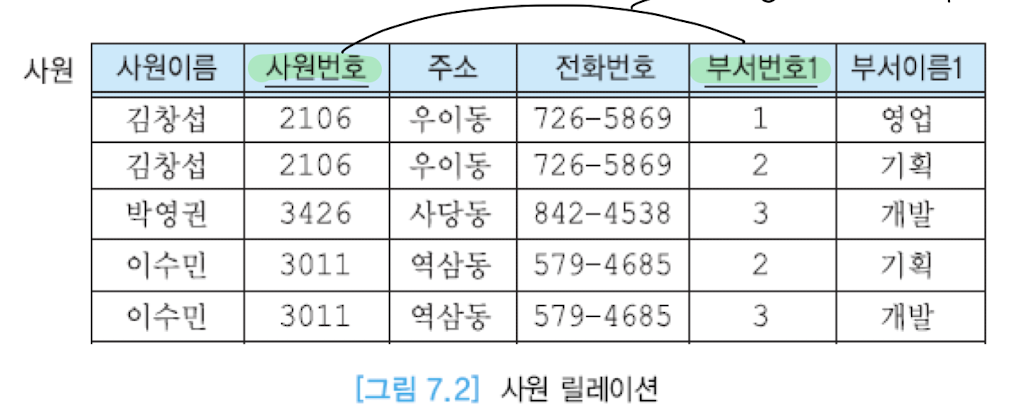
이 릴레이션에는 다음과 같은 문제점이 있다. 아마 위의 갱신 이상 항목과 비슷할것이다.

데이터의 중복
특정 사원이 여러 부서에 속해있을 경우, 사원 이름, 번호, 주소, 전화번호 등의 중복된 데이터가 불필요하게 저장된다.
삽입 이상
사원 이름, 주소 등 다양한 부가적 정보를 중복하여 저장하지 않으면, 그 사람의 부서 이름을 저장할 수 없다.
수정 이상
만약 부서 이름이 변경될 때, 그 부서에 속한 일부 인원들에 대한 튜플만 수정하면 데이터 불일치가 발생한다.
삭제 이상
만약 어떤 부서에 사원이 딱 한명 존재하는데, 위 릴레이션에서 그 정보를 삭제하면 해당 부서에 대한 데이터도 같이 삭제되어 릴레이션에 해당 부서의 데이터가 남아있지 않게된다.

그렇다. 부모님이 방 치우라고 잔소리 하시는데는 다 그럴만한 이유가 있어서 그런것이다. 이제부터 부모님 말씀을 잘 듣는 착한 어른이가 되도록 하자.

그렇다면, 이러한 문제점들을 어떻게 해결하는가?

정규화 종류

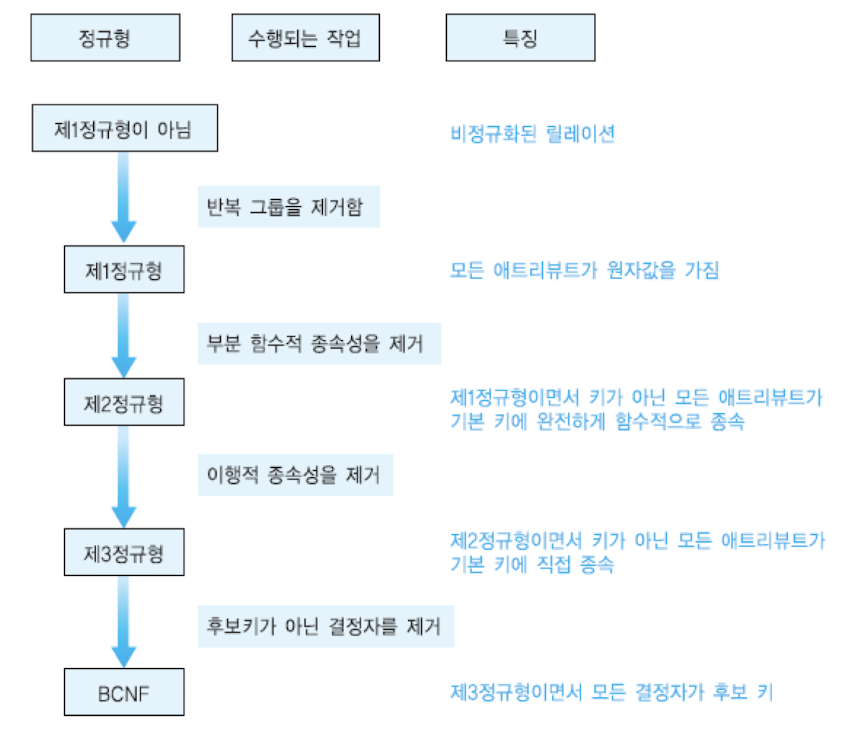
정규화에는 제 1~3 정규형, BNF 정규형, 제 4~5 정규형의 형태로 완성할 수 있으며, 보통 BNF 정규형 까지만 고려한다. 그러면 지금부터 제 1~3 정규형과 BNF 정규형을 알아보도록 한다.

1. 제 1 정규형

한 릴레이션이, 특정 애트리뷰트에 대해 원자값만 갖는 릴레이션 정규화 모델을 제 1 정규형이라고 한다.

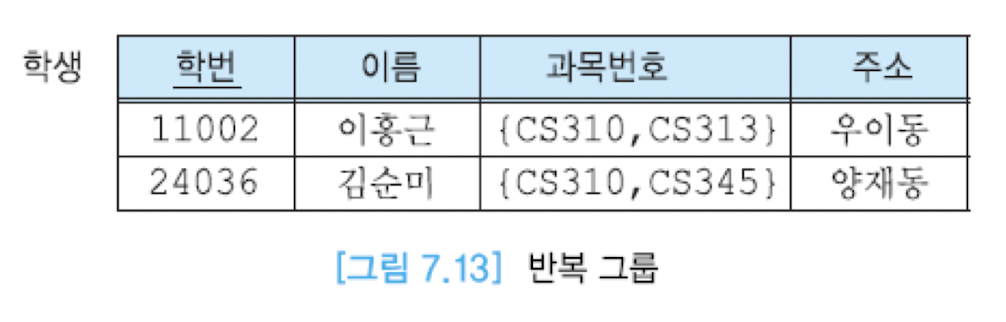
위의 릴레이션은 과목번호 애트리뷰트가 여러 값을 포함하도록 설계되어 있다. 이를 제 1 정규형을 만족하도록 설계하면 다음과 같다.

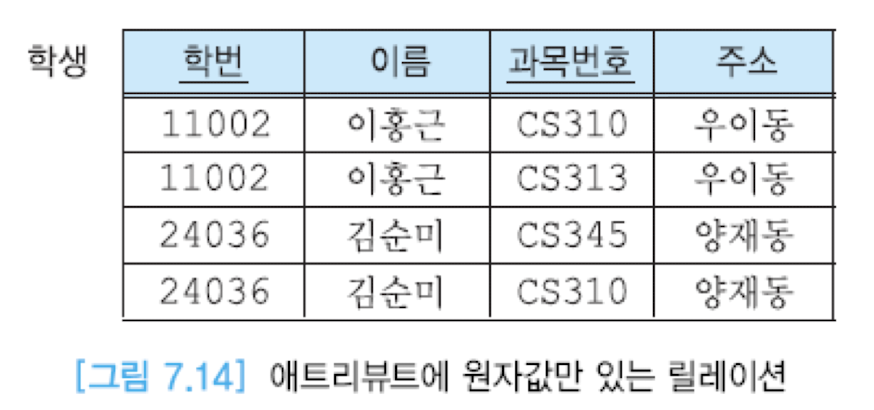
다만, 그림 7.14 처럼 분리했을 경우 여전히 갱신 이상이 존재한다. 우선, 특정 학생의 주소가 변경될 경우 중복되어 저장된 해당 학생의 모든 튜플에 대해 주소를 수정해주지 않으면 데이터 불일치가 발생할 수 있다.(수정이상) 또한 이름 데이터를 중복적으로 계속 입력해주지 않으면, 결정자 이외의 데이터(주소)를 삽입할 수 없다.(삽입이상) 마지막으로, 만약 단 한 과목만 수강하는 학생에 대해 그 수강 정보를 삭제해버리면 학생 릴레이션에서 그 학생에 대한 정보는 존재하지 않게된다.(삭제이상)

이러한 상태를 보완하기 위해, 제 2 정규형을 적용한다.

2. 제 2정규형

앞선 제 1 정규형에서 갱신 이상이 일어나는 이유를 함수적 종속성으로 설명할 수 있다. 함수적 종속성이 무엇인지 알아보자.

함수적 종속성
만약 애트리뷰트 A가 애트리뷰트 B의 결정자라면, B는 A에 함수적 종속성을 가진다.

이것이 바로 함수적 종속성의 정의이다. 이 때, 결정자와 피 결정자 모두 복수의 애트리뷰트일 수 있다.

그런데, 복수의 애트리뷰트가 결정자일 경우, 그 결정자의 진부분집합에 해당하는 애트리뷰트가 또 다른 애트리뷰트를 결정할 수 있다. 다음 그림을 보자.

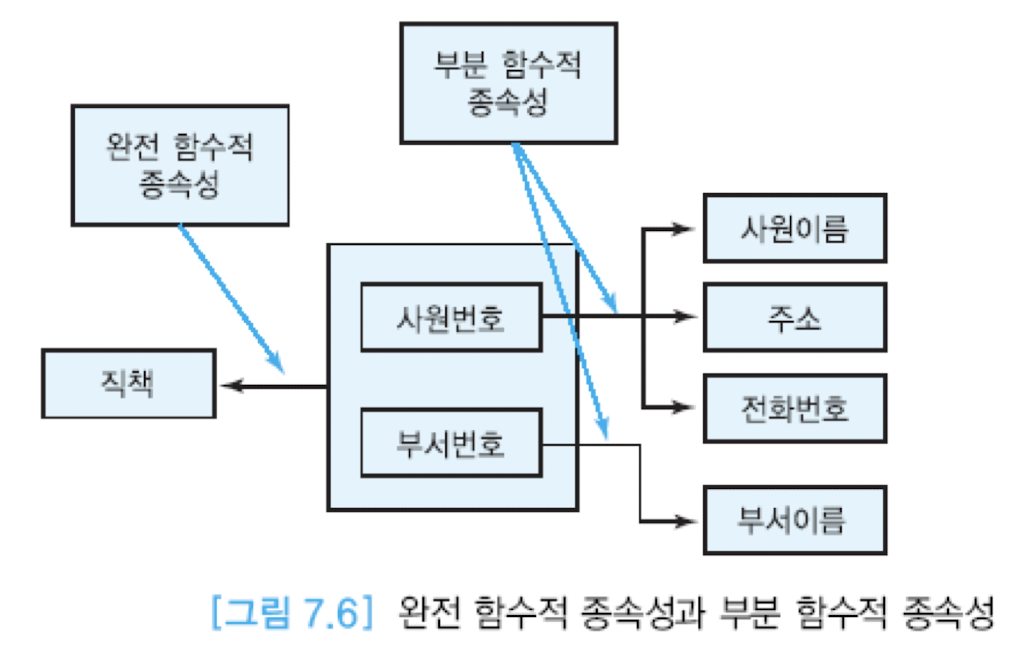
위 그림처럼, 결정자의 일부가 또 다른 애트리뷰트를 결정할 때, 이를 부분 함수적 종속성 이라고 한다.

그리고 A가 B를 결정하고, B가 C를 결정할 경우, C가 B를 통해 A에 대해 이행적 함수적 종속성을 가진다. 이는 다음 그림과 같다.

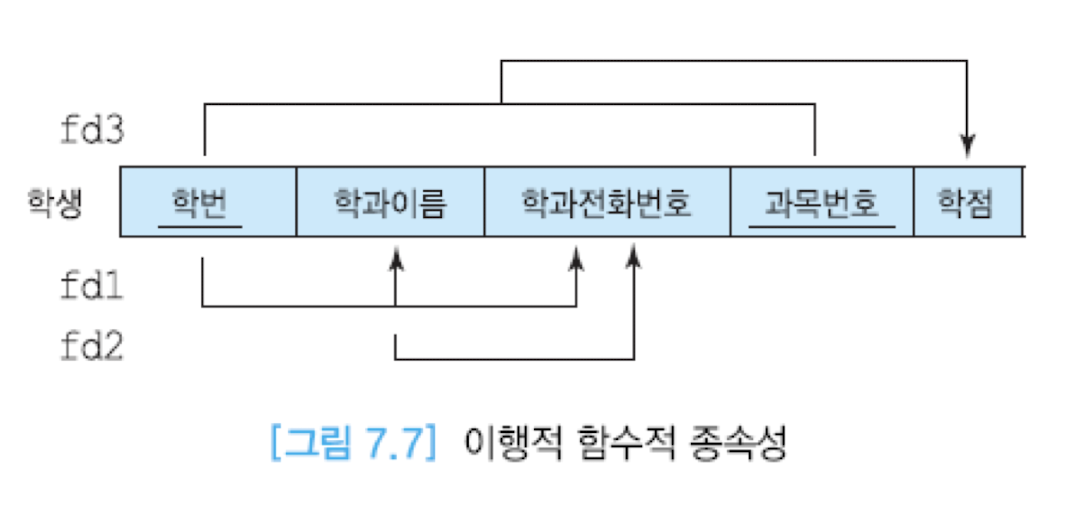
위의 fd2에 의해 학과 전화번호는 학번 애트리뷰트에 이행적으로 종속된다.
마찬가지로, 학과이름과 학과 전화번호는 학번에 부분 종속된다.

제 1정규형을 만족하더라도, 그 릴레이션에서 기본키에 대한 부분 함수적 종속성이 존재하면, 그 릴레이션은 갱신 이상이 일어난다. 제 2정규형에선 이런 부분들을 해결한다.

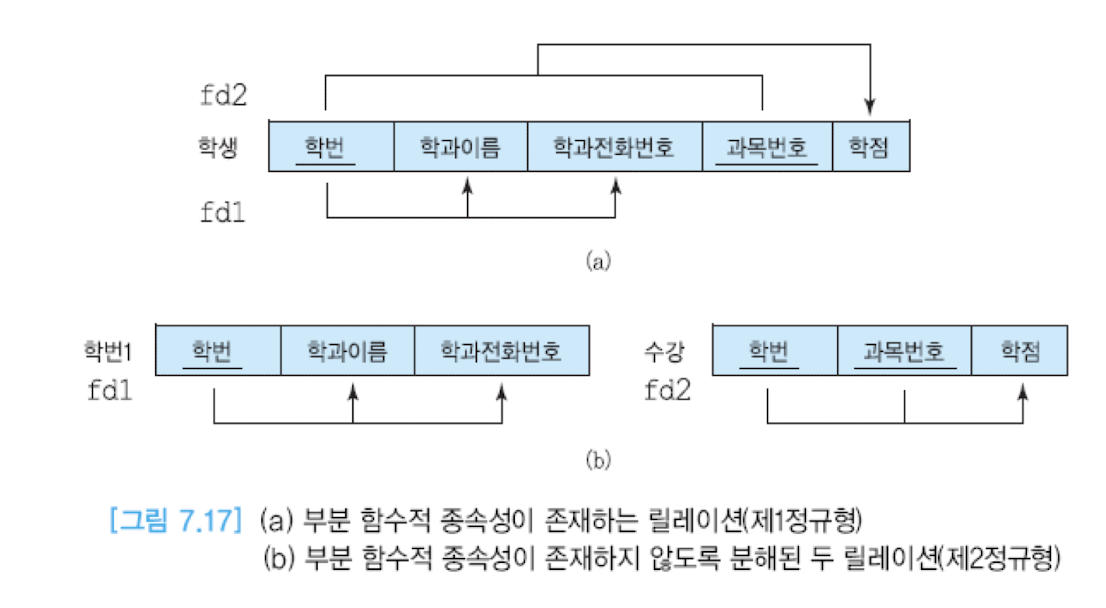
위의 그림처럼, 제 2 정규형은 후보키에 해당하지 않는 모든 애트리뷰트들이 결정자에 완전히 함수적으로 종속되면 그 형태를 만족시킬 수 있다. 예시 (b)는 적절하게 분리되어 제 2 정규형을 만족시키고, 부분 함수적 종속성이 없다.

다만 이 경우에도 갱신 이상은 존재하는데, 그 이유는 이행적 함수적 종속성이 완전히 해결되지 않았기 때문이다. 위의 그림 7.7을 보면, 사실 학번 뿐만 아니라 학과이름도 학과 전화번호를 결정한다. 즉, 학과 전화번호가 학과 이름을 거쳐 학번에 이행적 함수적 종속성을 가지는 것이다. 제 3 정규형에서는 이러한 것들을 분리한다.

3. 제 3 정규형

제 3 정규형은 제 2 정규형을 만족하며 이행적 함수적 종속성이 없는 릴레이션을 뜻한다. 위 그림 7.17의 학번1 릴레이션의 경우, 다음과 같이 분리하여 제 3정규형을 만들 수 있다.

다만, 이 제 3정규형에서도 갱신 이상이 발생할 수 있다. 다음의 예시를 보자.

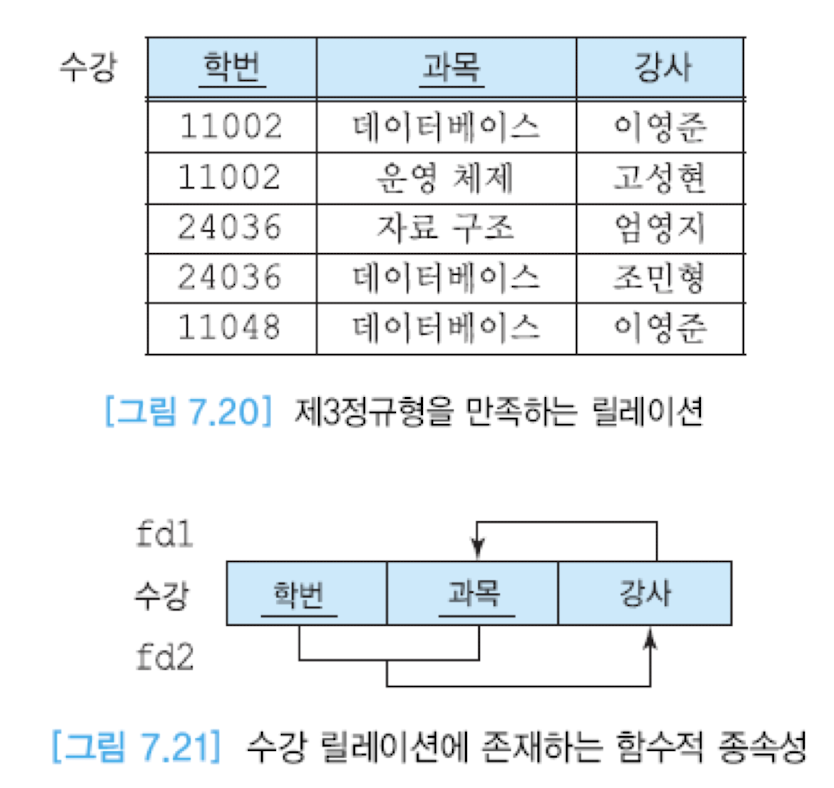
이 릴레이션에서는 키가 아닌 애트리뷰트가 다른 애트리뷰트를 결정하는 결정자인데, 이럴 경우 갱신 이상이 발생할 수 있다. (이 릴레이션에서 후보키는 (학번, 과목), (학번, 강사)인 복합 키라고 가정한다.)

그리고 이를 해결하기 위해 BCNF 정규형을 만든다.

4. BCNF 정규형

BCNF 정규형을 만족시키기 위해서는 제 3 정규형을 만족시키고 반드시 후보 키만 다른 애트리뷰트를 결정해야한다.

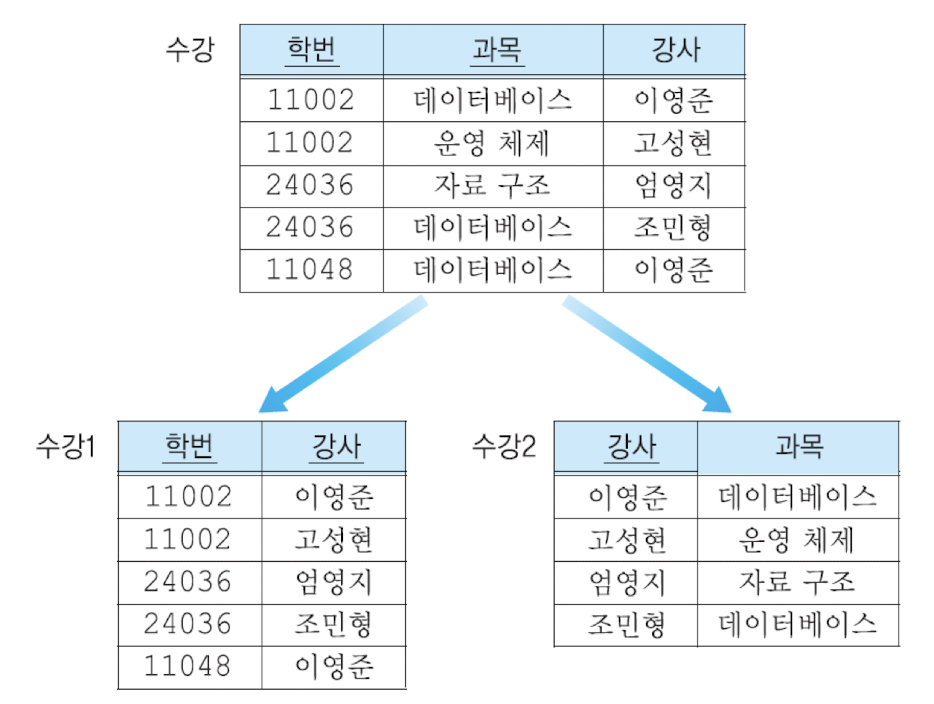
제 3 정규형 릴레이션을 BCNF로 만들기 위해서는, 우선 후보 키가 아닌데 다른 애트리뷰트를 결정하는 결정자와, 이에 의해 결정되는 애트리뷰트를 하나의 릴레이션으로 묶어 분리한다. 그리고 그 결정자를 원래의 애트리뷰트에 남긴다. 이 결정자는 앞서 분리한 릴레이션에 접근하는 외래키 역할도 하게 된다.
그 예시는 다음과 같다.