시간복잡도??
알고리즘 문제를 풀면서 효율적으로 풀 수 있을까 고민한 적이 있다. 이거는 시간복잡도를 고민한다는 말이라고한다. 나는 그냥 게을러서 그렇게 생각하는줄 알았는데 이게 더 효율적으로 생각하는 방법이라니 아주 좋다.
그렇다면 시간복잡도를 고민한다는 것은 무엇을 의미 할까?
입력값의 증가 or 감소에 따라 시간이 어떻게 비례하여 증가 or 감소하는가
오호 그러니까 어떤 함수에 인자를 50개에서 100개로 두배 늘렸을 때 시간이 똑같이 두배가 늘어났느냐 아니면 다르게 증가 혹은 감소했는가를 보는거다!
그래서 우리는 효율적인 알고리즘을 짜기 위해서 시간복잡도로 평가한다.
Big-O??
Big-O표기법은 시간복잡도를 표기하는 방법이다.
이렇게까지 하는 이유는 최악의 상황을 고려하여 대비하기 위해서다.
그렇다면 어떤 Big-O의 표기법이 있을까?
O(1)
이건 무엇일까? 입력값이 늘어남에 따라 시간이 상수이다? 이는 일정하다는 것을 의미한다. 그래서 constant complexity라고 부르며, 입력값이 증가해도 시간은 늘어나지 않음을 의미한다. 예시를 들어보자
function constantComplexity(arr, index){
return arr[index];
}
let arr = [1,2,3,4,5];
let index = 3;
let result = constantComplexity(arr, index);
console.log(result) // 4위의 예시를 보면 변수 arr의 값이 늘어나도 즉시 출력값을 불러낼 수 있다.
O(n)
고등학교 수학시간이 생각이 많이 난다. 물론 경제수학시간때도 배운거 같다.하하하.
O(n)은 입력값이 늘어날때 같은 비율로 늘어남을 의미한다. 그래서 linear complexity라고 부른다. 보통 loop가 한개 있으면 이렇게 O(n)이 된다. 물론 loop를 어떻게 사용하냐에 따라 달라지겠지?
예시를 들어보자
function linearComplexity(n){
for(let i = 0; i < n; i++){
// n이 늘어남에 따라 시간도 n이 늘어나는 비율로 늘어난다~
}
}O(log n)
이건 로그가 있다. 그래서 logarithmic complexity라고 한다. 대표적인 예시로 BST(Binary Search Tree)가 있다. 쉽게 생각해서 술자리에서 하는 up & down 게임을 생각하면 된다. 이게 이렇게 효율적인 게임이였다니.. 암튼 O(log n)은 O(1)다음으로 빠른 시간 복잡도를 가진다.
O(n^2)
느낌이 온다. 이건 아마도 입력값에 비례하여 시간이 제곱수로 늘어 날 것이다. 정답! 그래서 우리는 이것을 quadratic complexity라고 부른다.
예시를 보자.
function quadraticComplexity(n){
for(let i = 0; i < n; i++){
for(let j = 0; j < n; j++){
// 이건 계산을 n*n만큼 하기 때문에 시간도 걸린다.
}
}
}아. 여기에서 n^3, n^4 또한 O(n^2)라고 표기한다. 이유는 n이 커질수록 지수가 주는 영향이 점점 퇴색때문이라고 한다.
O(2^n)
이건 가장 느린 알고리즘이라고 한다. 왜냐면 입력값이 커질수록 말도안되게 커지기 때문이다. 그래서 우리는 exponential complexity라고 부른다. 이 알고리즘의 대표적인 예시로 재귀로 구현한 피보나치 수열이 있다.
보자보자 어디보자.
function fibonacci(n){
if(n<=1){
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}실제로 브라우저에서 돌려보게 되면 코드줄 수에 비해 시간은 정말 오래걸린다. 허허허
정리
이상 고등학교 수학시간이였다. 오랜만에 다시 정리하면서 하니까 재미있었다. 그때는 나도 수학을 정말 잘했었지...
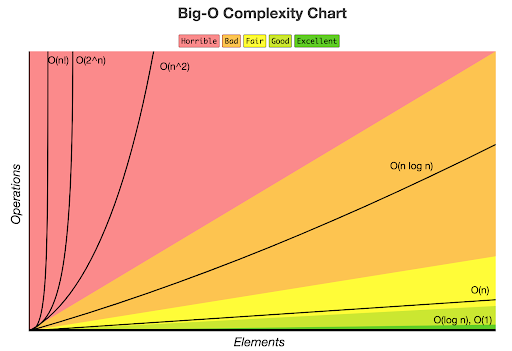
시간복잡도는 최악을 대비하기 위해서 필요하다. 그래서 알고리즘을 짤때 항상 이것을 염두에 두고 생각을 해야겠다. 보다 효율적인 알고리즘을 짜기 위해서..