- 정규화(Normalization)
관계형 모델에서는 정규화 이론이라는 DB 설계 이론이 있습니다. 정규화 이론은 RDB(관계형 데이터베이스)를 효율적으로 사용하기위해 필요하며, 관계형 모델을 전제로 구축된 DB 설계 이론입니다.
정규화의 가장 큰 장점은 모순을 방지한다는 점입니다.
모순이란 논리적으로 불일치한 데이터가 발생한 상황을 의미하며, 모순이 발생한 상태를 변칙(Anomalies)라고 합니다.
예를 들어, 다음과 같은 릴레이션이 있다고 가정합니다.

victolee는 1학년일까요? 3학년일까요?
릴레이션은 참인 명제의 집합이므로, 두 데이터 모두 참입니다. 즉, victolee가 1학년인지 3학년인지 명확히 알 수 없는 '변칙'이 발생한 상태입니다.
모순이 생기는 가장 큰 원인은 데이터의 중복입니다. 이러한 문제는 '정규화'를 통해 데이터 중복을 제거함으로써 해결할 수 있습니다. 즉 정규화는 '릴레이션 내에서 중복을 제거하는 과정'을 의미합니다.
정규화(데이터 중복 제거)를 통해 얻을 수 있는 장점은 다음과 같습니다.
- 응용프로그램 단계에서 불필요한 로직을 제거
- 올바른 데이터만 얻을 수 있다.(변칙방지)
- 불필요한 쿼리(예를 들어, 서브쿼리) 제거로 성능 향상
- 정규형(Normal Form, NF)
정규화 과정이란 각각의 정규형이 되기 위한 조건들을 충족시키는 과정을 말합니다. 정규형에는 단계가 있습니다. 높은 단계로 갈수록 중복이 적은 릴레이션이 설계 됩니다.
- 제1정규형(1NF)
- 제2정규형(2NF)
- 제3정규형(3NF)
- 보이스코드 정규형(BCNF)
- 제4정규형(4NF)
- 제5정규형(5NF)
- 제6정규형(6NF)
다음은 단계별 각 정규형의 특징입니다. - 높은 단계의 정규형은 그 이전 정규형의 조건을 만족해야 합니다.
- 예를 들어, 4NF는 1NF~BCNF의 정규형 조건을 기본적으로 만족해야 합니다.
- 핵심 정규형은 BCNF, 5NF이며, 그 외 정규형을 목표로 하지 않습니다.
- 일반적으로 BCNF를 만족하면 5NF를 만족하는 경우가 많기 때문에 BCNF를 목표로 두기도 합니다.
- 특히 6NF는 직교성을 다룰 때 유용하지만, 릴레이션이 너무 많아져 불필요한 join이 많아지므로 6NF를 목표로 두진 않습니다.
- 2NF~BCNF는 함수 종속성을 제거를 통해 만족하게 되며, 4~6NF는 결합 종속성의 제거를 통해 이뤄집니다.
- 용어 정리
각 정규형이 어떤 조건들을 만족해야 되고, 이를 해결하는 과정을 보기 이전에 용어 정리를 하면 좋습니다.
- 슈퍼키(Primary Key, 기본키)
- 릴레이션에서 특정 튜플을 유일하게 구분할 수 있는 애트리뷰트의 조합을 가진 키
- 튜플을 유일하게 구분만 할 수 있으면 되기에, 슈퍼키는 여러 개 존재할 수 있습니다.
- 예를 들어, A, B, C 애트리뷰트가 있을 때 (A, B), (B, C) 조합만으로 튜플을 구별 할 수 있으면, 해당 조합이 슈퍼키가 됩니다.
- 후보기(Candidate Key)
- 슈퍼키 중에서 '최소한'의 애트리뷰트 조합으로 특정 튜플을 구분 할 수 있는 키
- 예를 들어, (A, B), (B, C) 슈퍼키가 존재 할 때, B 애트리뷰트만으로 튜플을 구별 할 수 있다면 , B는 후보키입니다. 즉 슈퍼키보다 후보키가 더 작은 범위 입니다.
- 진부분집합
- 관계형 모델은 수학의 집합론에 근거한 모델이기에 집합에 대한 개념이 필요합니다.
- 진부분집합이란 자신을 제외한 부분집합을 의미합니다.
- 예를 들어, {1,2}의 부분 집합은 {공집합, {1}, {2}, {1, 2}}이며, 진부분집합은 {공집합, {1}, {2}}입니다.
- 무손실분해(Lossless Decomposition)
- 정규화를 진행하는 과정에서 중복을 제거하는 방법으로 릴레이션을 분해합니다. 이 때 기존의 정보를 잃어버리지 않으면서 분해하는 것을 무손실 분배라고 합니다.
- 즉, 릴레이션을 분해 할 때 무손실 분해가 되어야 합니다.
- 무손실 분해가 되면 분해된 릴레이션을 join해서 기존의 정보를 다시 얻을 수 있습니다.
- 함수 종속성(Function Dependency)
- 임의의 릴레이션 R의 애트리뷰트 A, B가 있다고 할 때, 애트리뷰트 A의 값을 알면 애트리뷰트 B의 값도 알 수 있는 관ㅖ를 말합니다.
- 이 때 A의 값은 유일해야 하며, B는 중복되어도 상관 없습니다.
- 즉, 키의 값을 알면 다른 임의의 애트리뷰트 값을 구할 수 있는 것처럼, 키의 성질을 정의한 것이라 할 수 있습니다.
- 결합 종속성(Join Dependency)
- 어떤 릴레이션이 여러 개의 릴레이션으로 무손실 분해가 가능하다면, 즉 여러 개의 릴레이션 결합으로 기존의 릴레이션을 만들 수 있는 관계를 의미합니다.
- 예를들어, A, B,..., N 릴레이션이 R의 스키마의 부분집합이라고 할 때, A, B,..., N 릴레이션을 결합한 결과와 R이 같은 경우 결합 종속성을 만족하게 됩니다.
- 직교성(Orthogonality)
- 여러 개의 릴레이션 사이의 중복 제거에 관한 개념입니다.
- 정규화는 한 개의 릴레이션 내부에서 중복을 없애는 데 초점을 맞춘 과정인 반면, 직교성은 DB 전체에서 중복을 제거하는 과정입니다.
이제는 각 정규형에 대해 알아보겠습니다.
일반적으로 BCNF를 목표로 하기 때문에 BCNF까지 자세히 설명하고 그 이후에는 개략적인 설명만 하겠습니다.
- 제1 정규형(1NF)
제 1 정규형이 되기위한 조건은 '테이블이 아닌 릴레이션이 어야 한다' 입니다.
테이블과 릴레이션은 비슷하지만 다른 개념입니다. 다음 조건을 통해 테이블은 릴레이션이 될 수 있습니다.
- 테이블에는 칼럼이나 행에 순서가 존재하지만, 릴레이션에는 순서가 존재하지 않습니다.
- 중복되는 튜플이 없어야합니다.
- 구체적인 값을 가져야 합니다. 즉 NULL 값도 안됩니다.
- 값은 의미가 있는 한 묶음의 데이터, 즉 원자 단위여야 합니다.(원자성)
- 원자 단위란 각 행마다 한 칼럼에 하나의 값을 가지는 것을 의미합니다.
- 예를 들어, 주소라는 칼럼에 "시, 도, 상세주소"를 몽땅 저장하는 것은 원자성에 위배됩니다.
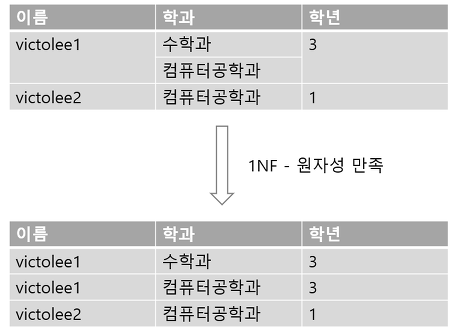
- 제2 정규형(2NF)
2NF는 후보키의 진부분집합에서 키가 아닌 속성에 대해, 부분 함수 종속성을 제거하는 작업입니다.
즉, 릴레이션이 1NF 조건을 만족하고 부분 함수 종속성을 가지지 않으면 2NF입니다.
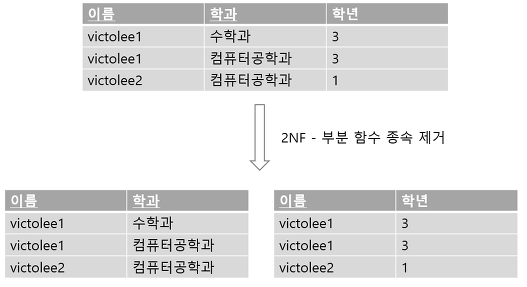
위의 예제에서 정규화를 하기 전 테이블을 보면, 이름과 학과는 후보키 입니다.
후보키 중 하나인(진부분집합) 이름을 알면 학년을 알 수 있으므로 함수 종속이 존재하고 있습니다. 2NF는 이러한 함수 종속을 제거하는 작업입니다.
함수 종속을 제거하려면 원래의 릴레이션을 무손실 분해시켜야 합니다.
- 종속 관계가 있는 속성만 추출해서(projection, 프로젝션) 새로운 릴레이션을 만듭니다.
- 즉 이름과 학년을 애트리뷰트로 갖는 새로운 릴레이션을 생성합니다.
- 기존에 있던 원래 릴레이션은 떨어져나간 애트리뷰트 학년을 제외한 릴레이션으로 존재합니다.
함수 종속을 제거함으로써 이렇게 두 개의 릴레이션으로 쪼개지고, 두 릴레이션을 결합하면 원래의 릴레이션이 되므로 무손실 분해가 이뤄졌습니다.

- 제3 정규형(3NF)
3NF는 추이 함수 종속성(Transitive Dependency)을 제거하는 작업입니다.
추이 함수 종속성은 키가 아닌 애트리뷰트 사이의 함수 종속성을 의미합니다.
예를 들어, 키가 아닌 애트리뷰트 X, Y가 있고, X를 알면 Y값을 알 수 있는 함수 종속성이 있다고 가정해보겠습니다. 3NF는 X와 Y사이의 함수 종속성을 제거하는 과정입니다.
2NF는 후보키와 키가 아닌 애트리뷰트 사이의 함수 종속성을 제거했다는 점에서 차이가 있습니다.

참고로 슈퍼키를 알면 X를 알 수 있고, X를 알면 Y를 알 수 있으므로 추이 함수 종속성이라는 말이 붙었습니다.
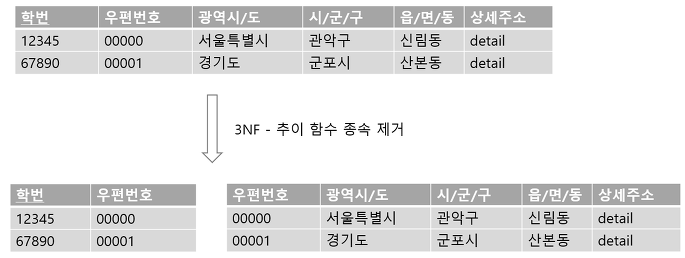
.png)
