알고리즘 문제풀이
1.[알고리즘] 물병 백준 1052 python
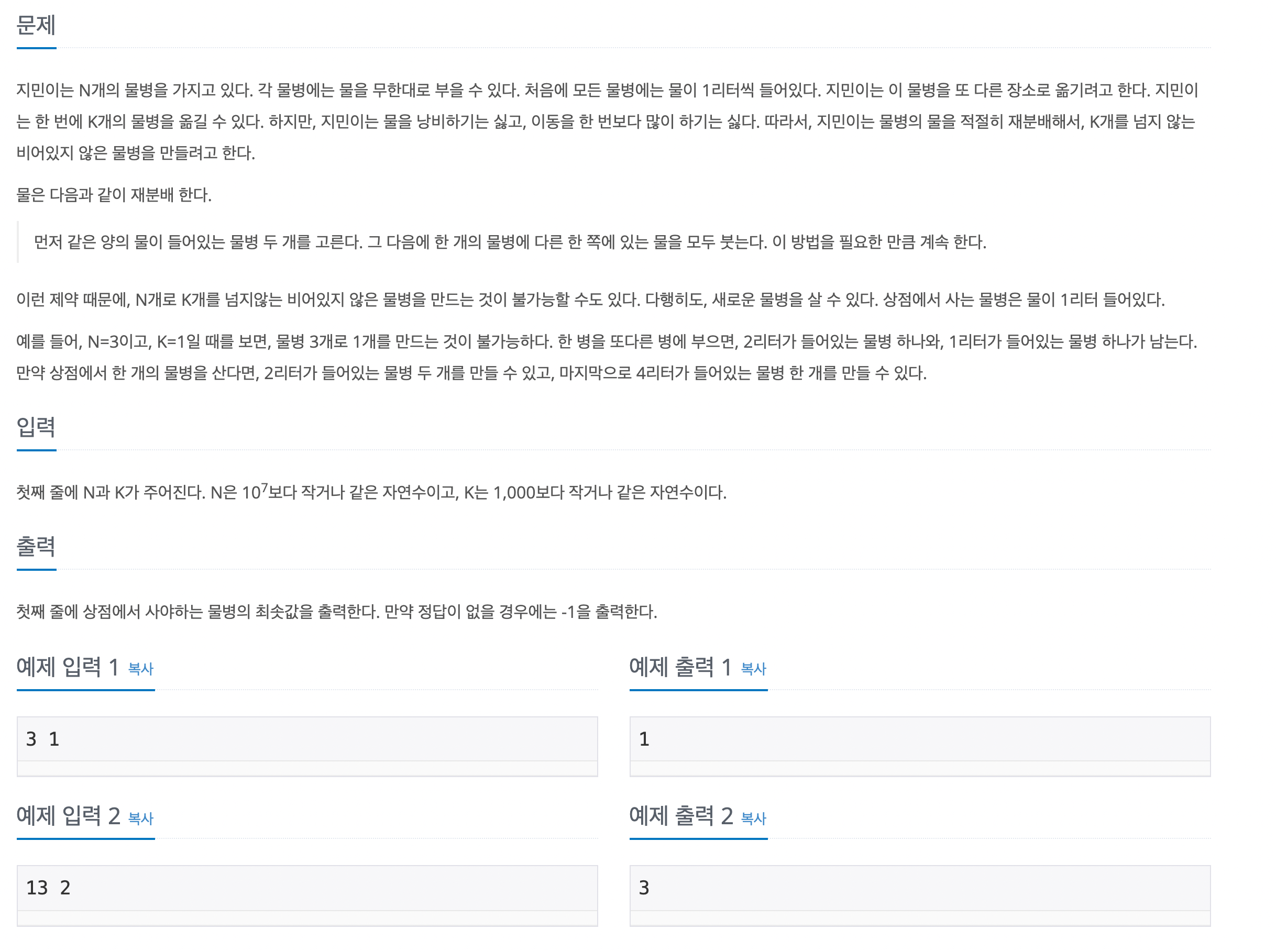
문제 바로가기풀이예제입력 2를 살펴보면1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1= 8, 4, 1더이상 물통을 합칠 수 없다.상점에서 물통을 사면8, 4, 1, 1=8, 4, 2더이상 물통을 살 수 없으므로8, 4, 2, 1한병 더 사면8, 4,
2.[알고리즘] 팔 백준 1105 python
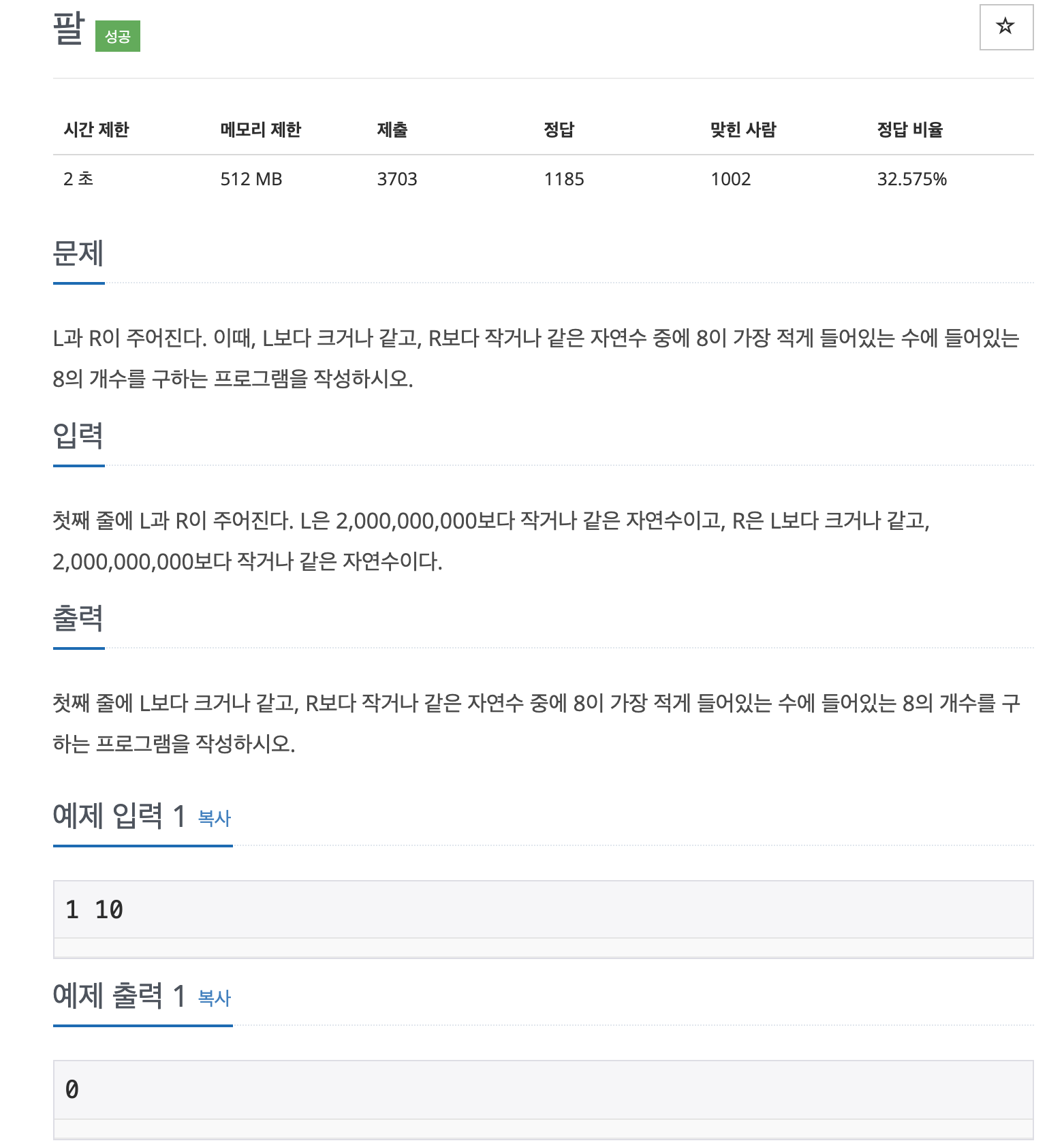
문제 바로가기규칙을 찾아야하는 그리디 문제.먼저 자릿수가 다르다면?\-> 8이 들어가지 않는 수는 무조건 있는 것을 알 수 있다.또한, 가장 큰 자릿수가 L과 R 둘 다 8이 아니라면 그 사이에 8이 들어가지 않은 수는 무조건 존재한다.\-> 가장 큰 자릿수부터 그 다
3.[알고리즘] 보석도둑 백준 1202 python
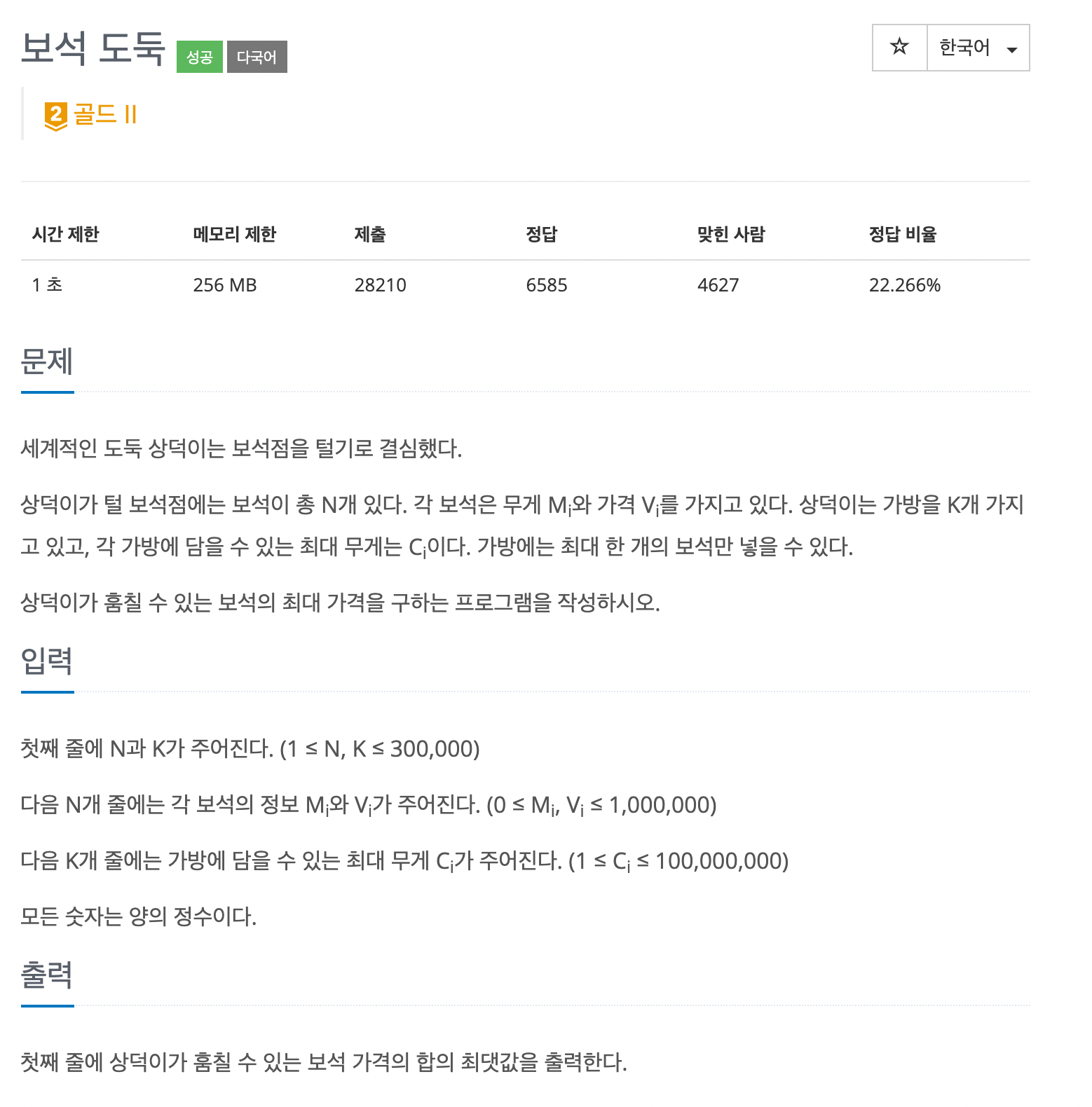
문제 바로가기가장 작은 용량의 가방에 넣을 수 있는 가장 비싼 보석을 넣어야 한다.따라서 기준을 가방의 용량(오름차순)으로 잡고 시작한다.가방의 용량을 오름차순으로 정렬하고 거기에 들어갈 수 있는 보석들을 전부 고른 후 가장 비싼 보석을 가방에 담는다.골라진 보석들은
4.[알고리즘] 그리디

그리디 알고리즘은 단순 무식하게 탐욕적으로 푸는 알고리즘이다.탐욕적이란, '현재 상황에서 지금 당장 좋은 것만 고르는 방법'을 의미한다.방법을 체화해서 다른 문제에도 적용할 수 있는 다른 알고리즘 기법과는 달리 그리디는 문제가 다양하기 때문에 암기한다고 해서 항상 잘
5.[알고리즘]DFS와 BFS

2차원 배열로 그래프의 연결 관계를 표현하는 방식2차원 리스트로 구현을 함a 노드에서 b 노드로 가는 비용을 grapha,b에서 알 수 있다. 리스트로 그래프의 연결 관계를 표현하는 방식링크드리스트로 구현을 함 -> c++이나 java의 경우는 linkedlist 라이
6.[알고리즘] 효율적인 해킹 백준 1325 python
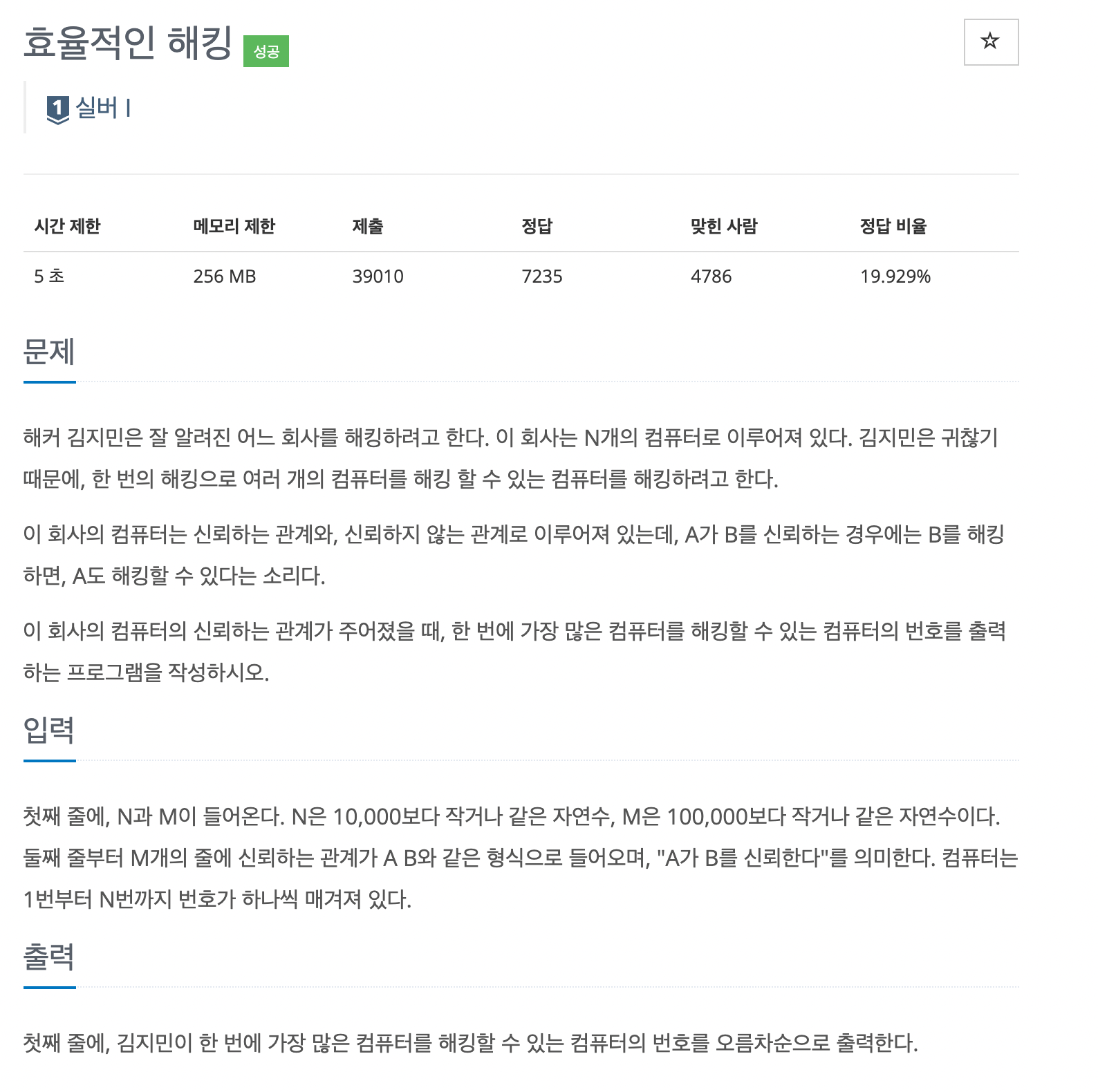
문제 바로가기 풀이 가장 작은 용량의 가방에 넣을 수 있는 가장 비싼 보석을 넣어야 한다. 따라서 기준을 가방의 용량(오름차순)으로 잡고 시작한다. 가방의 용량을 오름차순으로 정렬하고 거기에 들어갈 수 있는 보석들을 전부 고른 후 가장 비싼 보석을 가방에 담는다.
7.[알고리즘] 이진 탐색

이진탐색은 찾는 값이 있는 리스트의 중간에 있는 값과 찾으려는 값을 반복적으로 비교하여 탐색하는 알고리즘이다.따라서 찾는 값이 있는 리스트가 정렬이 되어 있어야만 사용할 수 있다.다음과 같은 리스트가 있다고 하고, 우리가 찾고싶은 값이 12라고 하자.1\. 리스트의 중
8.[알고리즘] 두 용액 백준 2470 python

문제 바로가기투포인터 문제입니다.보통 절대값이 비슷한 음수와 양수를 합쳐야 0과 가까운 수가 나오므로 배열을 정렬한 후 양쪽 끝에서부터 비교해나가면 되는 문제입니다.포인터 두 개를 왼쪽 끝과 오른쪽 끝으로 설정합니다.첫 값으로 answer에 맨 왼쪽과 오른쪽을 더한 값
9.[알고리즘] 합이 0인 네 정수 백준 7453 python
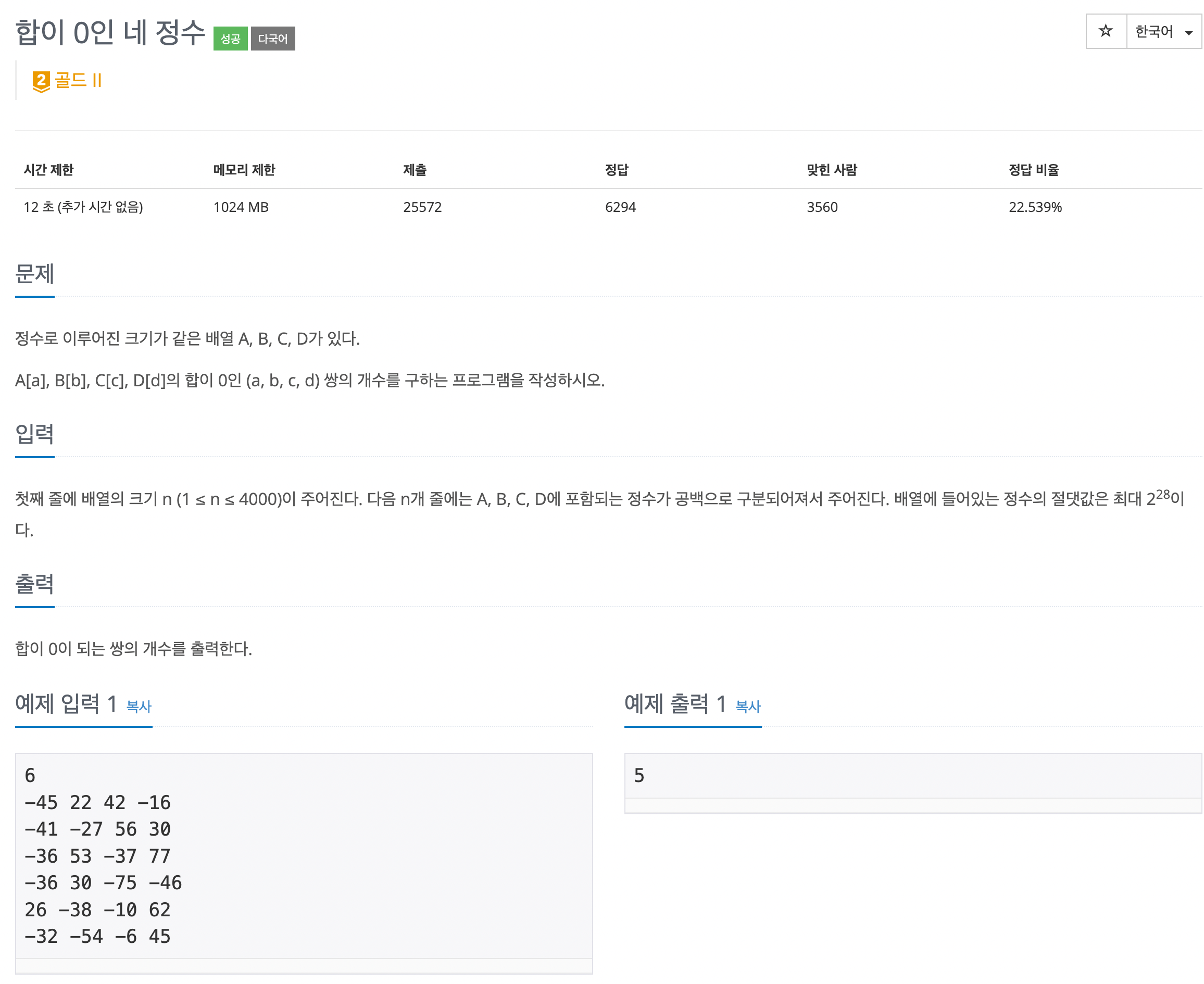
문제 바로가기완전탐색을 돌릴 경우 O(n^4)가 걸려서 풀리지 않을 게 보입니다. 배열 4개의 원소의 합이 0이 되도록 조합하는 문제이므로 두개의 배열의 원소의 합과 다른 두개의 배열의 원소의 합을 저장하고 부호를 비교하는 방법으로 진행하면 될 것 같습니다.또한 배열에
10.[알고리즘] 가장 긴 증가하는 부분 수열 3 백준 12738 python
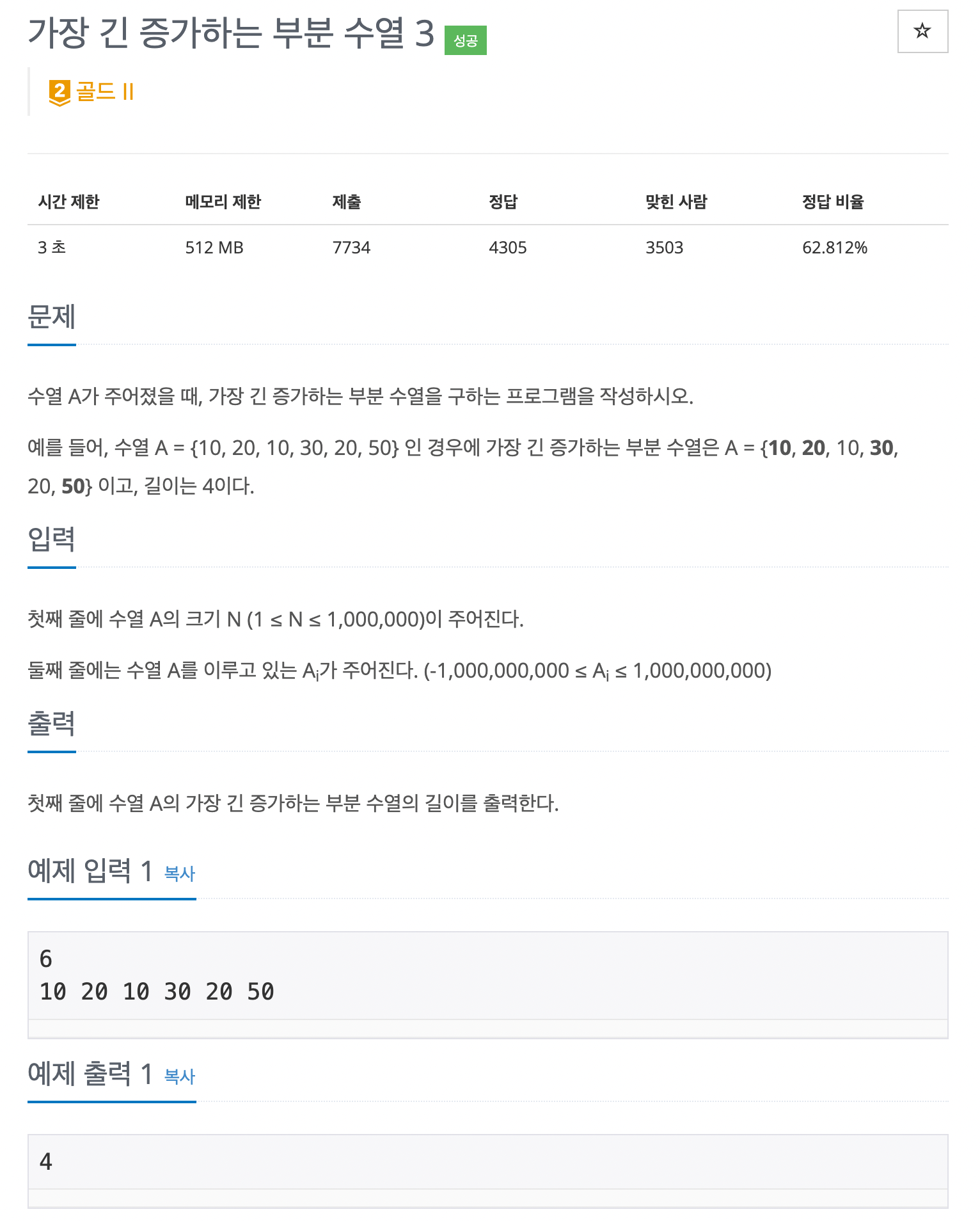
문제 바로가기증가하는 부분 수열이라는 말을 보고 LIS(최장 증가 부분 수열)알고리즘이 떠올라야합니다.배열 내에서 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그러한 부분 수열 중 길이가 가장 긴 수열을 LIS(최장 증가 부분 수열)라고 합니다. 해당 문제에서는
11.[알고리즘]다이나믹 프로그래밍(Dynamic Programming)

큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘피보나치 수열을 계산할 때 f(n)을 구하기 위해서 f(n-1)과 f(n-2)를 알아야 한다.f(n-1)을 알기 위해서는 f(n-2), f(n-3)을 알아야 한다.여기까지만 보더라
12.[알고리즘] 최단경로 1753 python
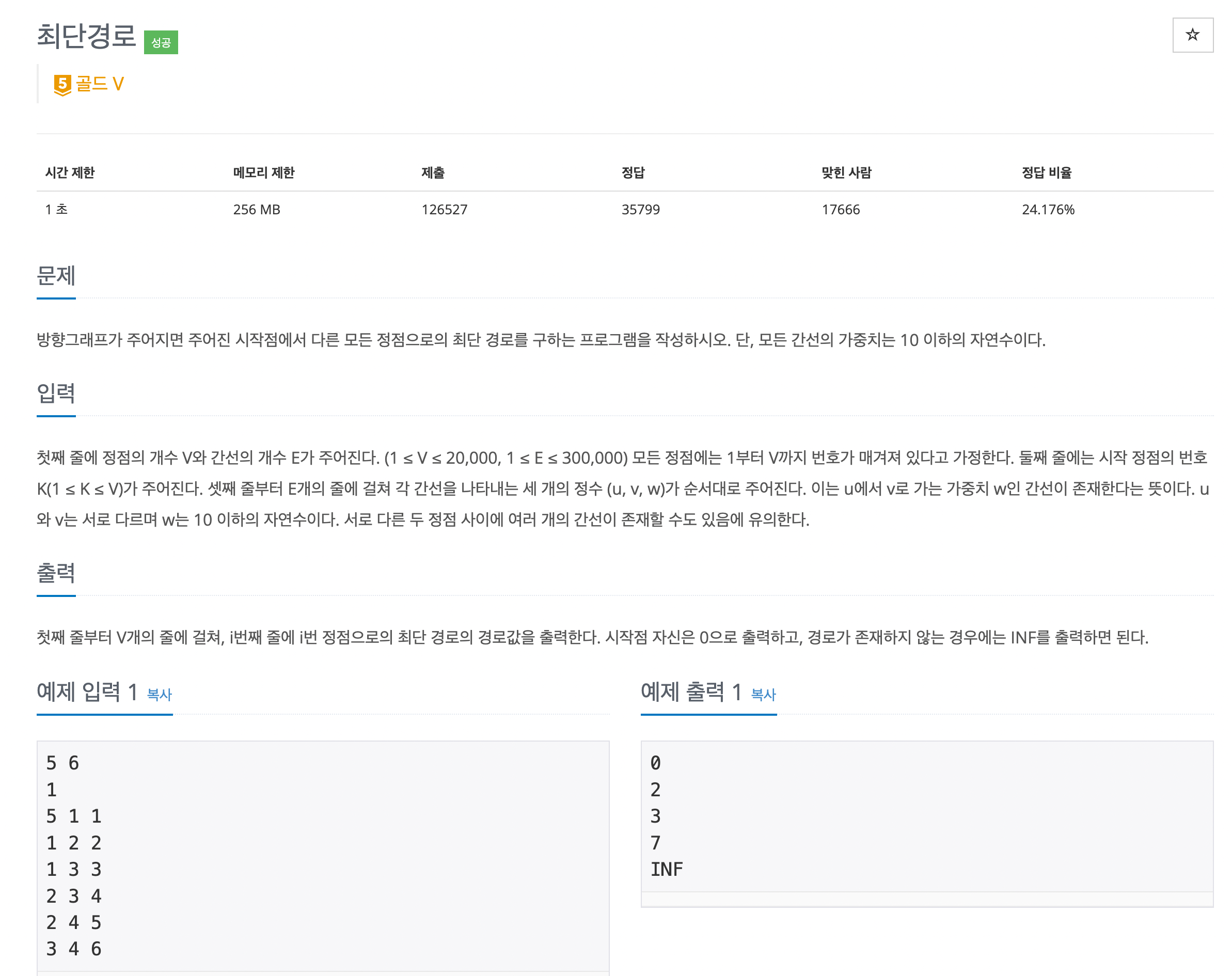
문제 바로가기최단경로 문제와 같이 간선의 길이까지 생각해야하는 문제는 보통 DFS로 풉니다.DFS 중에서도 최단경로 문제는 Dijkstra 알고리즘을 사용하는 경우가 많습니다.우리가 v라는 노드로 가고싶다면 u를 경유해서 v를 가는 거리바로 v를 가는 거리를 비교해서
13.[알고리즘] 특정한 최단 경로 1504 python
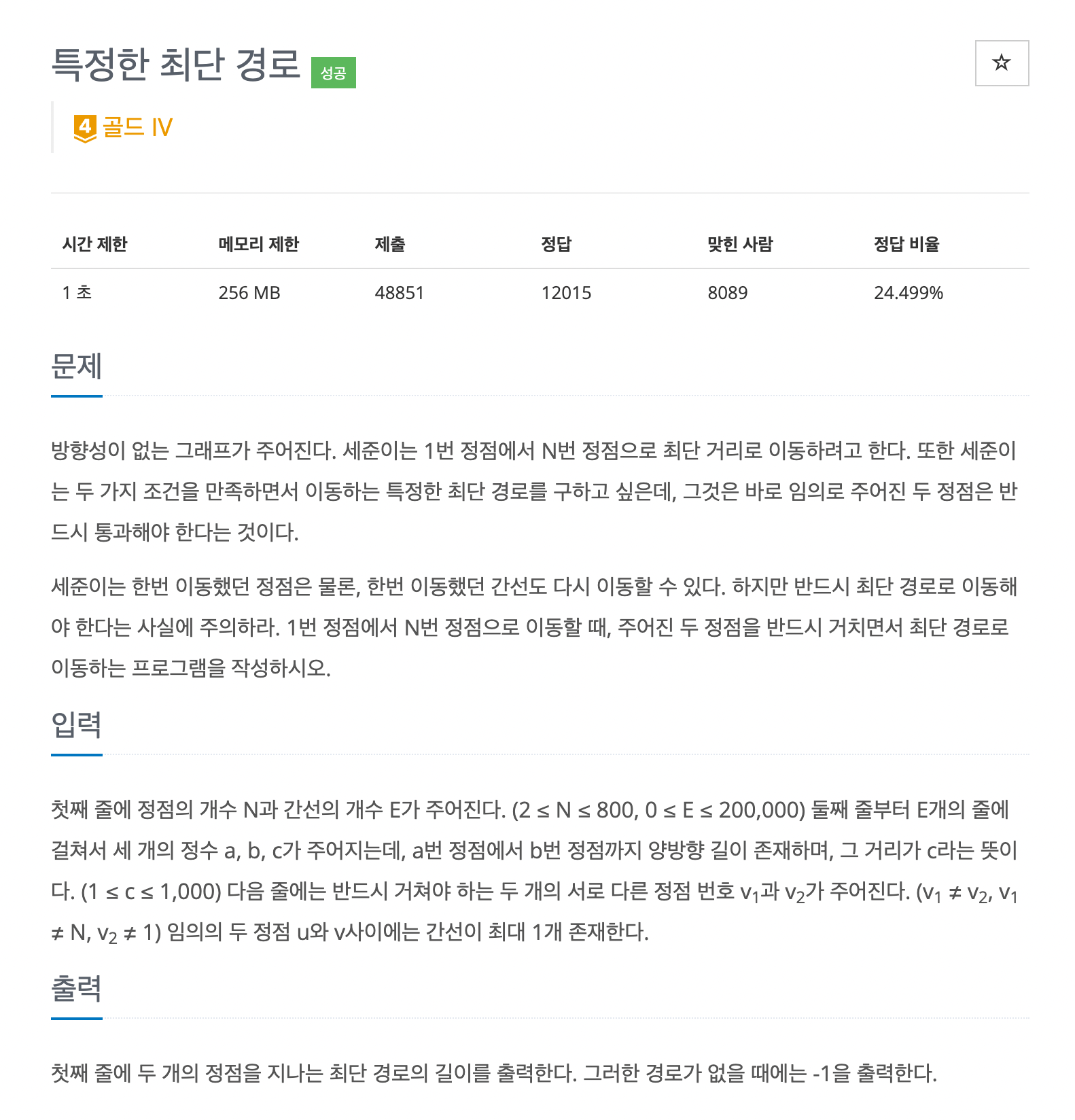
문제 바로가기최단경로 문제는 Dijkstra 알고리즘을 사용하는 경우가 많습니다.요 문제를 풀기 전에 근본 문제 요것을 먼저 풀어보시는 것을 추천드립니다.Dijkstra 알고리즘의 자세한 설명도 위 링크에 있슴니다!!!!!!기본적인 최단거리 문제에서 반드시 지나야하는