개요
- 알고리즘이란 문제를 해결하기 위한 절차
- 문제를 해결하는 방법에는 여러 가지가 존재할 수 있기 때문에, 알고리즘을 분석하고 비교할 줄 알아야 함
- 알고리즘을 분석하는 것은 컴퓨터 자원의 사용량을 분석하는 것
- 자원을 적게 사용할수록 효율적인 알고리즘
- 자원이란 실행 시간, 메모리 사용량 등을 말함
- 효율적인 알고리즘의 척도인 시간 복잡도와 공간 복잡도에 대해서 알아보자
시간 복잡도
- 알고리즘의 분석에 있어서 가장 중요한 부분은 실행 시간
- 알고리즘의 실제 실행은 하드웨어 및 소프트웨어 환경에 따라 천차만별이므로 단순 측정으로는 실행 시간을 분석할 수 없기 때문에, 하드웨어와 소프트웨어 환경을 배제한 객관적인 지표가 필요
- 이를 위해서 시간 복잡도를 사용
- 시간 복잡도는 알고리즘을 수행하는 데 필요한 연산이 몇 번 실행되는지를 표기
-
연산의 개수는 상수가 아니라 입력한 데이터의 개수를 나타내는 n에 따라 변함

-
위 3가지 Case의 알고리즘의 연산 횟수를 비교해보면 아래와 같이 나타낼 수 있음 (간단하게 나타내기 위해 루프 제어 연산은 제외)
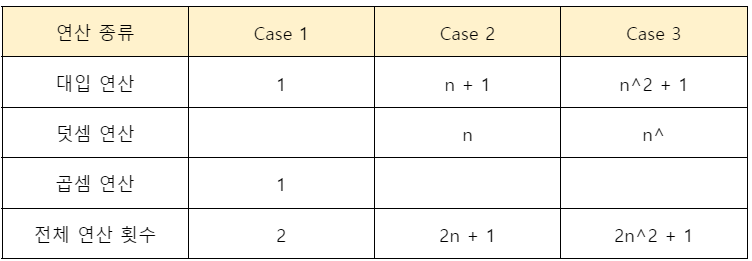
-
하나의 연산이 t만큼의 시간이 필요하다고 하면 이에 대한 시간 복잡도 함수를 각각 2t, (2n + 1)t, (2n^2 + 1)t 로 나타낼 수 있음
-
시간 복잡도를 구했으므로 알고리즘의 수행 시간을 측정할 수 있음
-
위의 예시를 바탕으로 입력값에 따라 어느정도의 시간이 걸리는지를 계산해보자 (편의상 모든 연산에 걸리는 시간은 1ms라고 가정)
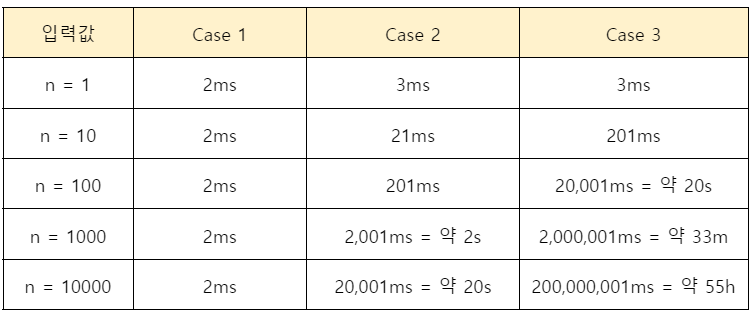
-
입력값이 작을 때는 차이가 크지 않았지만, 입력값이 커질수록 매우 큰 차이가 벌어진다는 것을 볼 수 있음
- 이를 실행 시간의 성장률(rate of growth)이라고 함
- 그래서 알고리즘을 효율적으로 구현하도록 늘 고민해야 함
Big-O 표기법
-
다항식의 시간 복잡도 함수에서 입력값이 커져감에 따라 각 항의 결과값에 관여하는 정도가 달라지게 됨을 알 수 있음
-
시간 복잡도와 공간 복잡도를 표시할 때는 각 함수의 모든 항을 표시하지 않으며 상수 계수와 중요하지 않은 항목을 제거한 점근적 표기법을 사용
-
점근적 표기법에는 Big-θ, Big-O, Big-Ω 등이 있지만 가장 많이 사용되는 것은 Big-O 표기법
-
Big-O 표기법은 점근적 상한선을 제공
-
앞선 시간 복잡도 함수를 Big-O 표기법으로 나타내면 각각 O(1), O(n), O(n^2)로 나타낼 수 있음
-
Big-O 표기법은 아래와 같으며 오른쪽으로 갈수록 상한선이 높아짐
-
왼쪽에 위치한 시간 복잡도일수록 해당 알고리즘은 빠르다고 할 수 있음
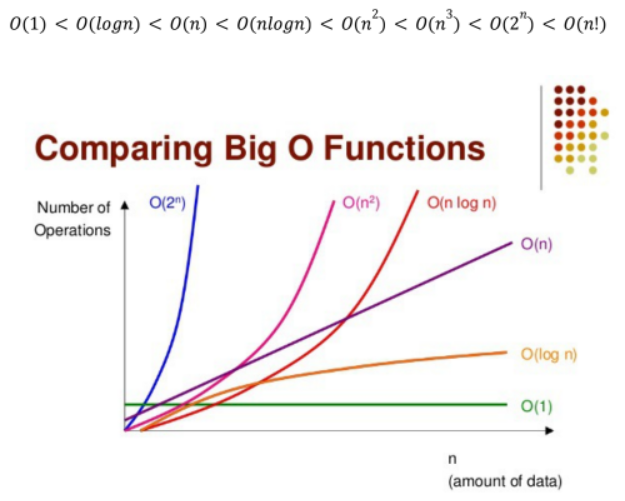
-
유의할 점은 한 알고리즘이 다른 알고리즘보다 실제로 빠르다고 하더라도 같은 방식으로 표현이 될 수도 있음
공간 복잡도
- 알고리즘의 성능을 측정할 때 실행 시간만을 따지지는 않음
- 공간 복잡도는 알고리즘을 수행하는 데 필요한 자원 공간의 양을 말함
- 공간 복잡도 함수는 고정 공간 요구 + 가변 공간 요구로 나타낼 수 있음
- 고정 공간 : 입력과 출력의 횟수나 크기와 관계 없는 공간
- 가변 공간 : 문제를 해결하기 위해 요구되는 추가 공간
분석하기
- O(n^2) 까지의 코드를 분석해보자
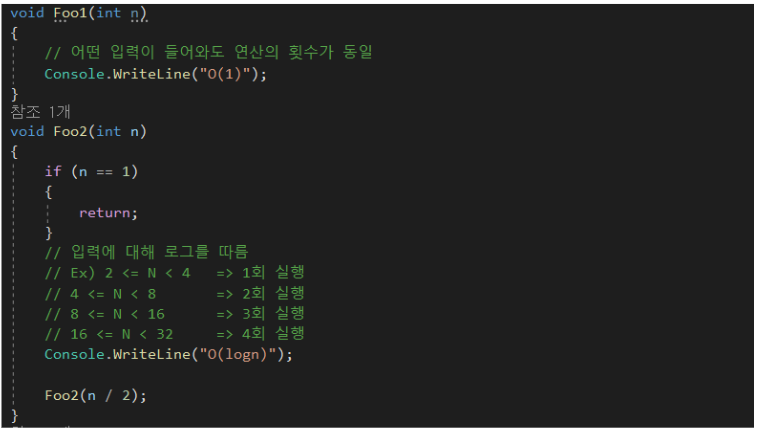


시간 복잡도 vs 공간 복잡도
- 효율적인 알고리즘은 실행 시간이 적게 걸리며, 자원을 적게 소모하는 것
- 하지만 시간은 공간과 반비례적인 경향이 있어 보통 알고리즘의 척도는 시간 복잡도를 위주로 판단
- 시간 복잡도를 위해 공간 복잡도를 희생하는 경우가 많음
최선,최악 평균의 경우
- 알고리즘을 분석할 때는 최선의 경우와 최악의 경우, 평균의 경우로 나눠서 파악
- 각각의 경우는 알고리즘의 효율성이 가장 좋을 때, 가장 나쁠 때, 평균적일 때
- 알고리즘 선택 및 개발 시 최선의 경우 혹은 평균의 경우는 매우 드물게 고려하며, 일반적으로는 최악의 경우를 고려함
- 그래서 점근적 상한선인 Big-O 표기법을 사용하는 것이기도 함