✅ 힙(Heap)?
힙 자료구조는 완전 이진 트리를 기초로 하는 자료구조입니다. 완전 이진트리는 마지막을 제외한 모든 노드에서 자식들이 꽉 채워진 이진트리를 말합니다.
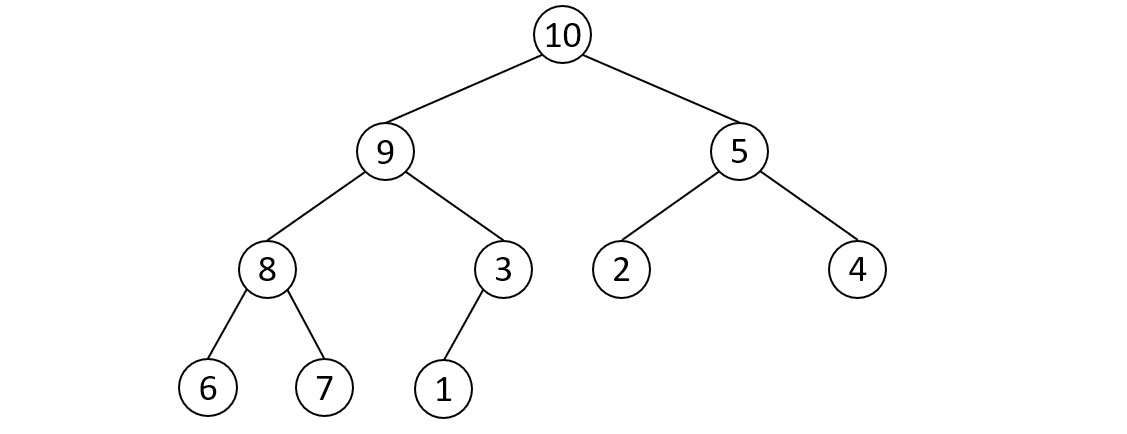
- 힙은 최대힙(Max heap)과 최소힙(Min Heap)으로 나눠집니다. - 최대힙은 부모노드의 값이 자식노드들의 값보다 항상 크고, 최소힙은 부모노드의 값이 자식노드의 값보다 항상 작습니다. (위 그림은 최대힙의 예시)
- 이러한 성질 때문에 항상 느슨한 정렬상태(반정렬 상태)를 유지합니다.
- 힙은 최댓값 또는 최솟값을 쉽게 뽑기 위한 자료구조 임으로 중복을 허용합니다.
✅ 힙을 배열로 구현하기
힙은 대체적으로 배열로 구현됩니다. 완전이진트리를 기본으로 하기 때문에 비었는 공간이 없어 배열로 구현하기에 용이합니다.
아래 그림과 같이 루트노드를 배열의 0번 index에 저장하고, 각 노드를 기점으로 왼쪽 자식노드는 a[i∗2+1], 오른쪽 자식노드는 a[i∗2+2] 의 index에 저장됩니다. 또한 특정 index의 노드에서 부모노드는 a[(i−1)//2]로 찾을 수 있습니다.
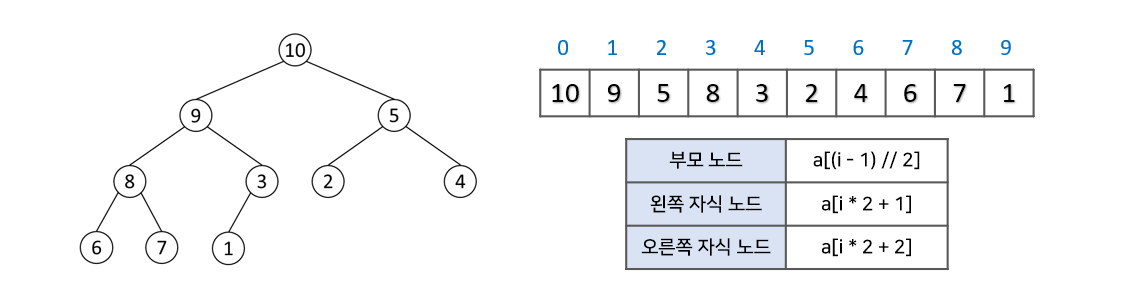
✅ 삽입과 삭제로 깨진 힙을 재구조화하기(heapify)
최대힙의 부모노드는 항상 자식노드의 값보다 크다는 조건을 가지고 있습니다. 하지만 힙에서 삽입 또는 삭제가 일어나게 되면 경우에 따라 최대힙의 조건이 깨질 수 있습니다. 이러한 경우에 최대힙의 조건을 만족할 수 있게 노드들의 위치를 바꿔가며 힙을 재구조화(heapify) 해주어야 합니다.
삽입과 삭제의 경우 모두 연산 자체는 O(1)로 작동하지만 heapify의 과정을 거치기 때문에 O(logn)의 시간복잡도를 가지게 됩니다.
✔ 삽입 과정 구현과정
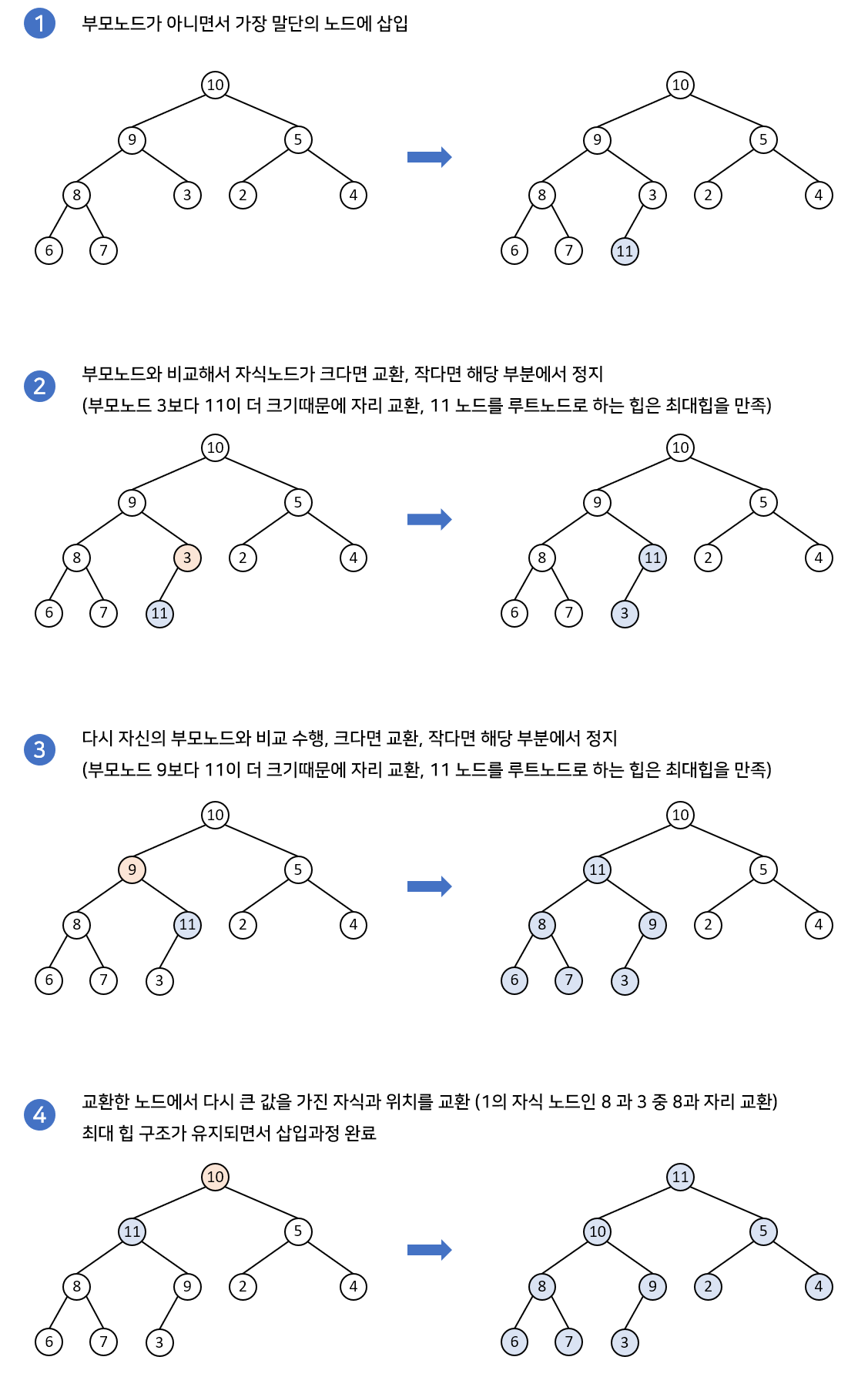
✔ 삭제과정 구현과정
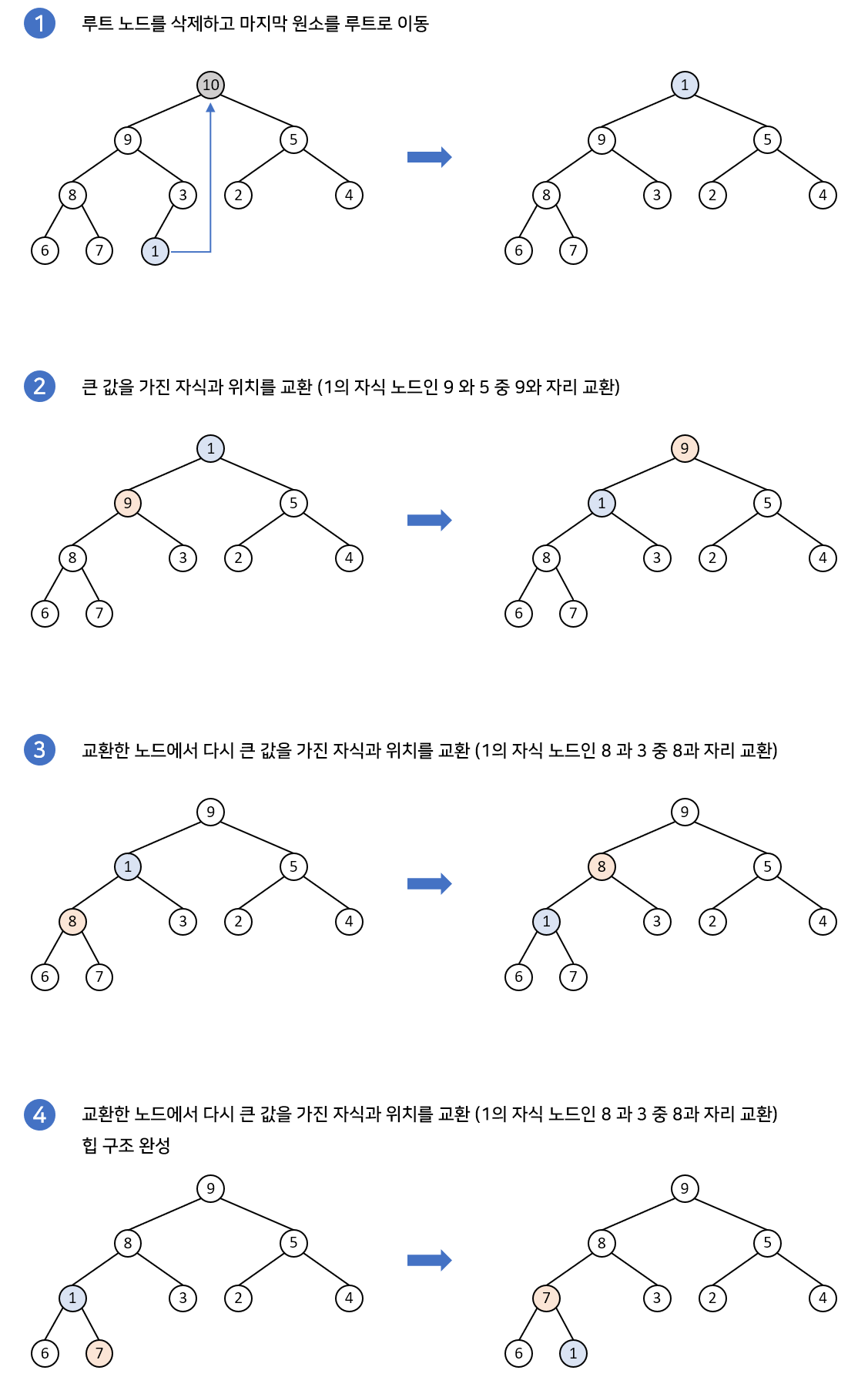
![]
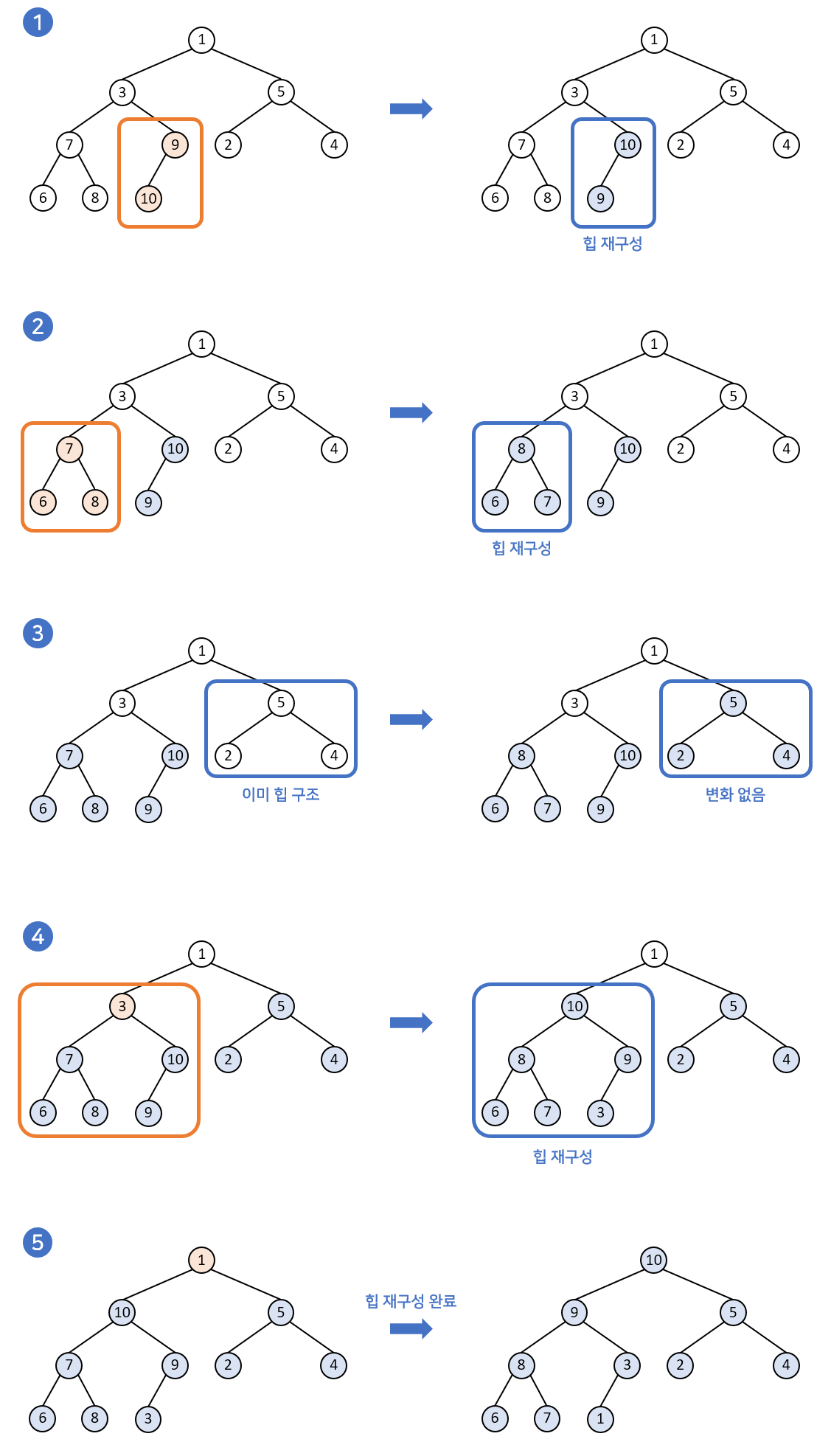
✅ 힙이 아닌 배열을 힙으로 만들기(build heap)
heapify의 경우 기본적으로 힙을 만족하는 경우에서 삽입 또는 삭제가 발생할 때 O(logn)의 시간복잡도로 다시 힙으로 만드는 과정입니다. build heap은 이와 다르게 아예 힙의 조건을 만족하지 않는 배열을 힙으로 만드는 과정입니다. 여러번의 heapify 과정을 거치기 때문에 결과적으로 시간복잡도는 O(nlogn)입니다.
✔ 재귀함수를 이용한 재구조
def make_heap(array, index, heap_size):
parent = index
left_child = 2 * parent + 1
right_child = 2 * parent + 2
if left_child < heap_size and array[left_child] > array[parent]:
parent = left_child
if right_child < heap_size and array[right_child] > array[parent]:
parent = right_child
if parent != index:
array[parent], array[index] = array[index], array[parent]
make_heap(array, parent, heap_size)
# 부모노드가 되는 노드들만을 골라서 뒤에서부터 heapify를 차례로 실행
for i in range((N - 1) // 2, -1, -1):
make_heap(array, i, heap_size)