🟣 시간복잡도
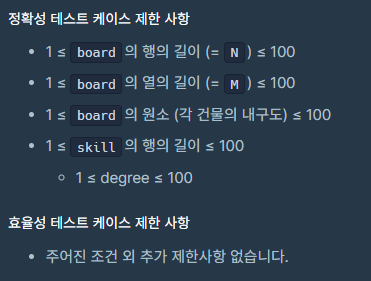
정합성 테스트의 완전탐색으로 했을 때 경우 행 * 열 = 10000에서 각각의 칸마다 skill의 최대 갯수인 100번 만큼 업데이트가 된다고 생각하면 1000000로 충분히 시간안에 들어올 수 있는 크기 였다. 하지만 효율성 테스트에서는 시간초과
🟢 사용한 알고리즘 : imos
- 정해진 구간 내에 시작과 끝이 포함된 부분 집합에 대한 명령이 여러개 들어올 때, 반복적으로 연산하게 되면 연산 시간이 매우 커질 수 있다.
- imos법은 각 명령에 대해 시작점과 끝점만 설정해 준 뒤, 마지막에 한 번의 반복을 통해 값을 계산하는 방식으로 구현할 수 있다.
1차원 배열에서의 imos

5에 -2 넣는 이유는 나중에 prefixSum으로 더해줄때
0 2 2 2 2 0 0 0 0 0 이렇게 결과가 나오는데 5번째를 0으로 만들어줌과 동시에 2 넣어줄 범위를 지정해주게 되는것이다.
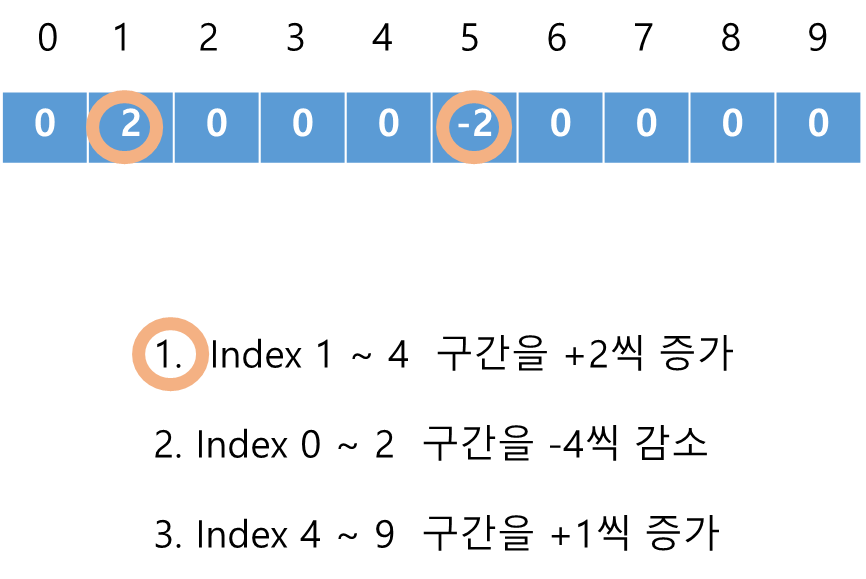
최종적으로 아래처럼 됨
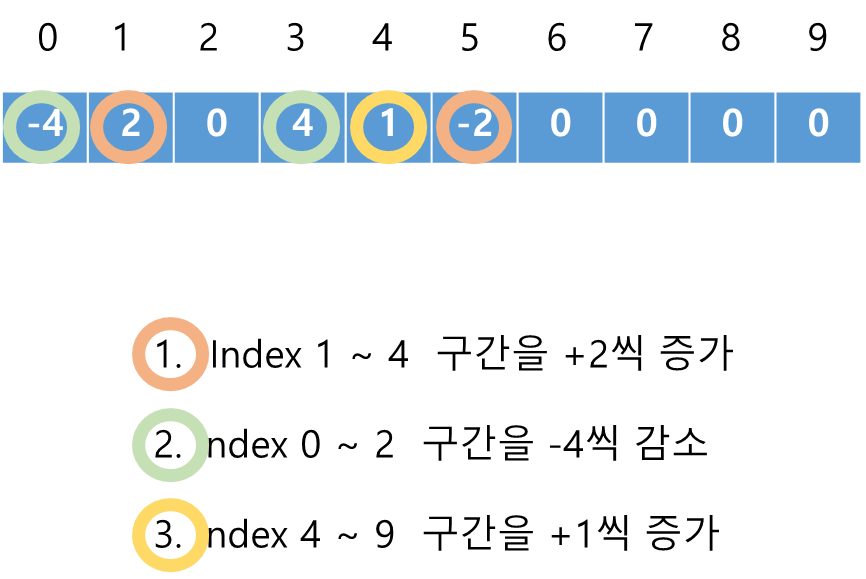
최종적으로 앞에서부터 PrefixSum으로 더해주면 결과끝

2차원 배열에서의 imos
- 매 사각형마다 한칸씩 배열의 값을 업데이트 시켜주면 너무 느림
- 사각형으로 바뀌어도 기본적인 아이디어는 같다. "시작과 끝만 기록한다"
- 단 2차원에서는 차원이 늘어난 만큼, 가로 방향으로 시작과 끝, 세로 방향으로 시작과 끝 두 번 기록하고, 시뮬레이팅할 때도 가로로 한번, 세로로 한번 prefixSum을 구하면 된다.
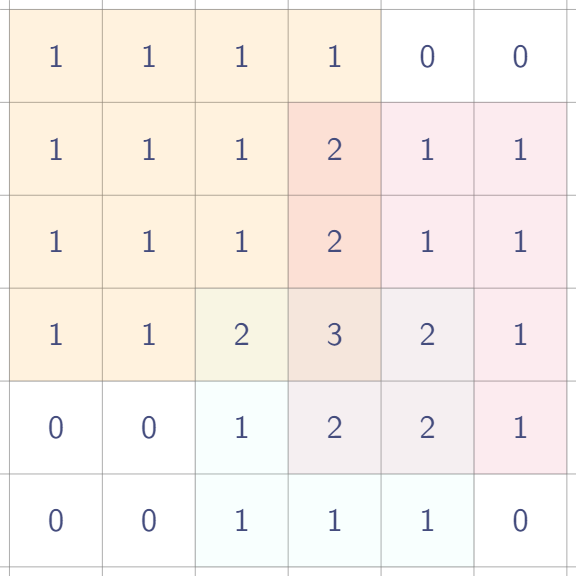
아래와 같이 나오기 위해서 어떻게 시작과 끝을 기록해 둬야하는지 살펴보자.
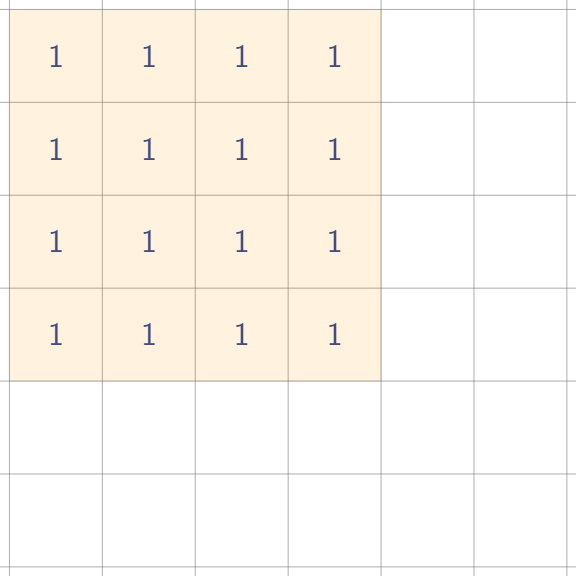
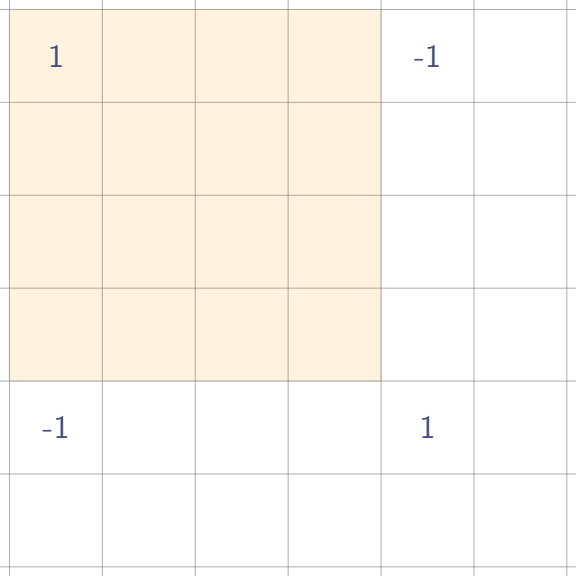
결론적으로 말하면 다음과 같이 4개의 점을 찍어두면 된다.
먼저 가로방향으로 prefixSum을 구한다.
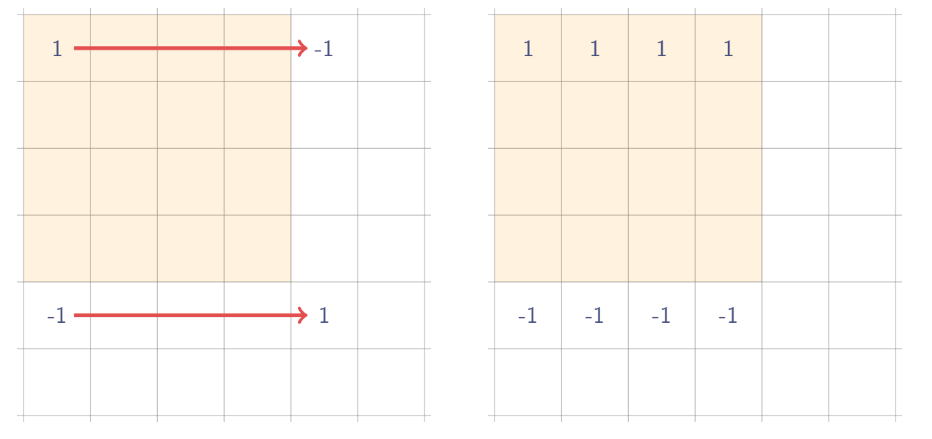
세로방향으로 마찬가지로 prefixSum을 구한다.
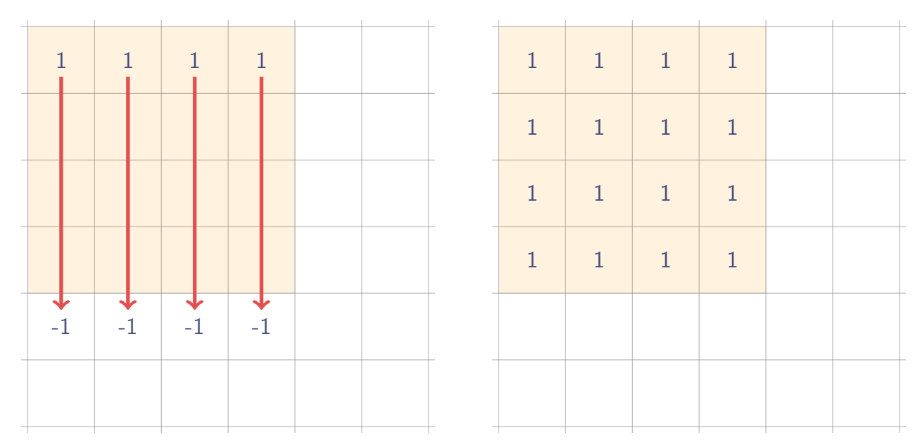
아까봤던 사각형에서도 적용해보자.
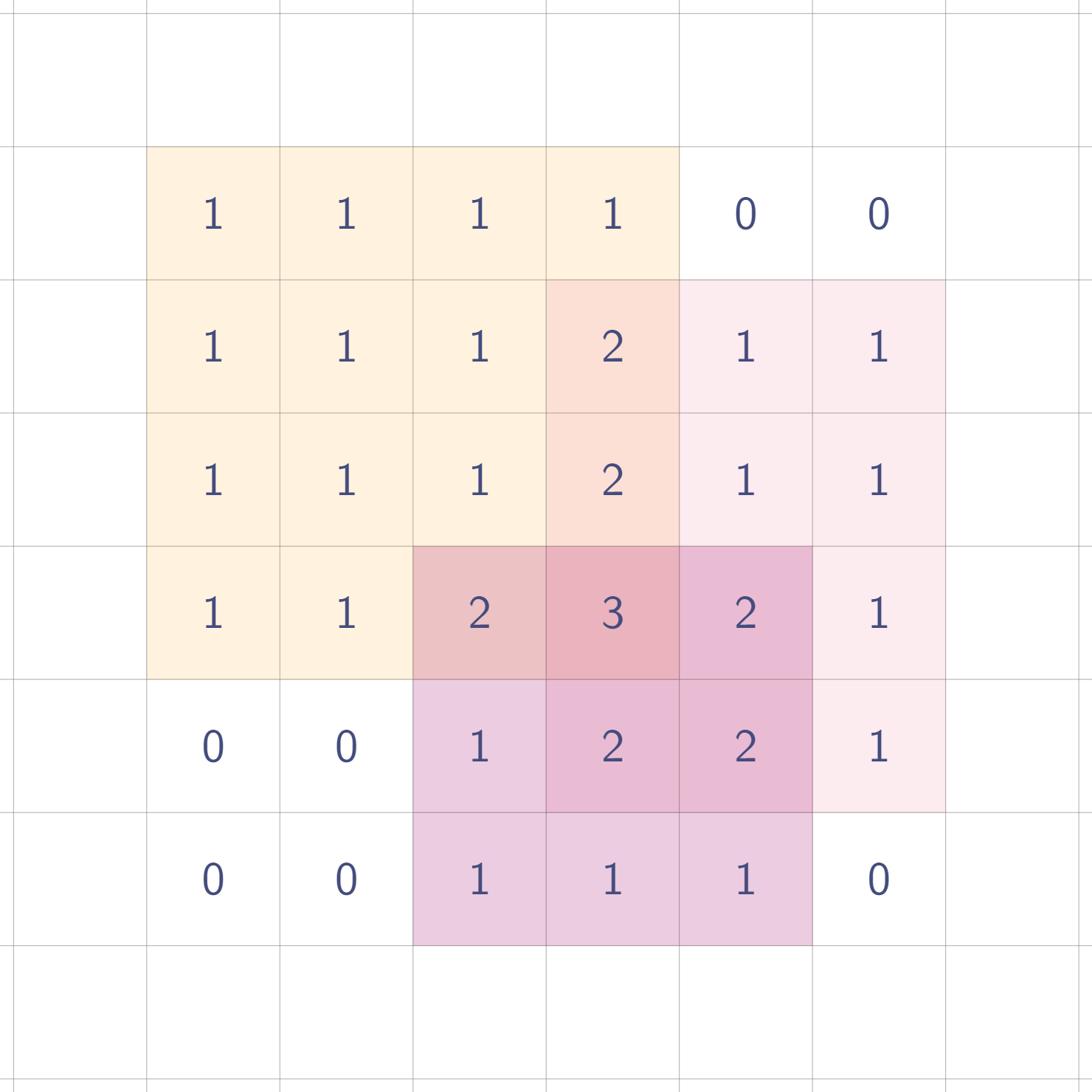
각 사각형들에 대해 실제로 1을 모두 찍는 게 아니고, 값 4개만 제대로 찍어두고 나중에 두 번 휩쓸면 되는 것이다.
사각형 영역은 총 3개이다. 각 사각형들에 대해 값을 찍으면 이렇게 된다.
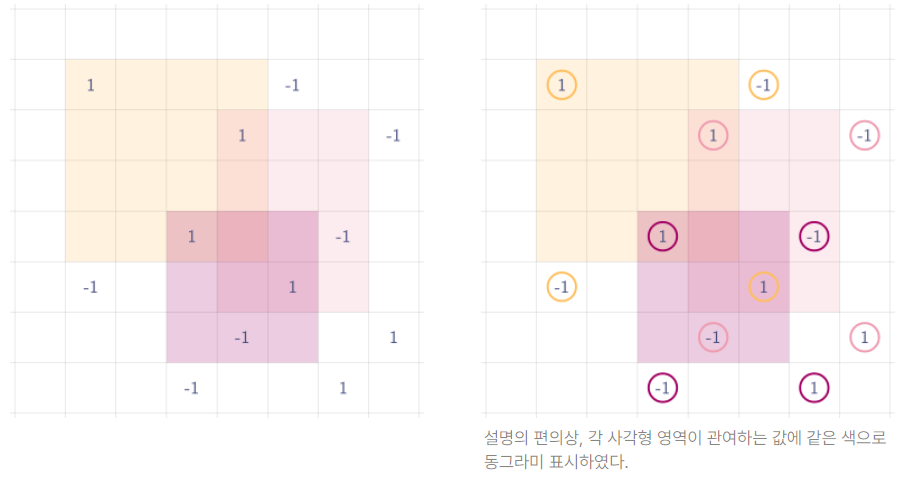
오른쪽으로 prefixSum을 구하면 아래와 같이 된다.
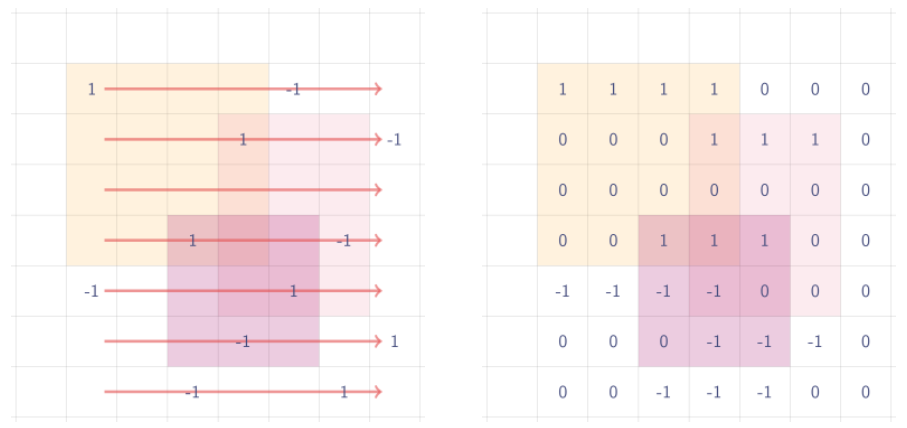
아래로 prefixSum을 구하면 최종결과가 나온다.
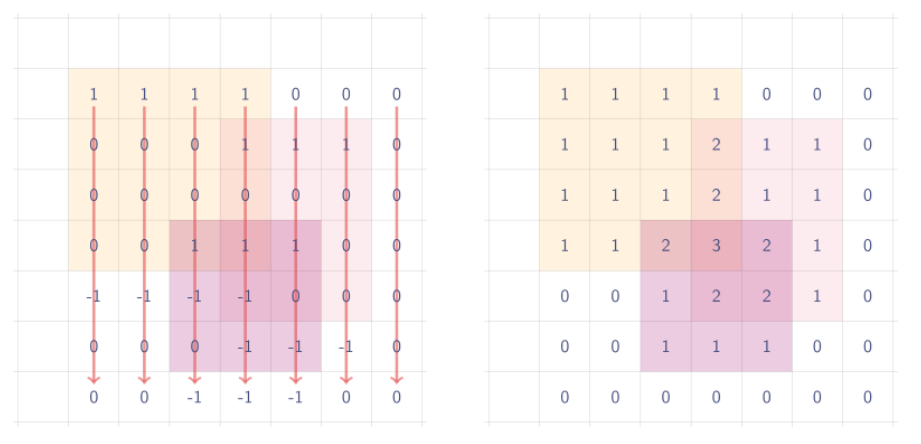
🟡 풀이방법
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.lang.reflect.Array;
import java.util.*;
public class Main {
static int[][] query;
public int solution(int[][] board, int[][] skill) {
int answer = 0;
int n = board.length;
int m = board[0].length;
query = new int[n][m];
for (int i = 0; i < skill.length; i++) {
int r1 = skill[i][1];
int c1 = skill[i][2];
int r2 = skill[i][3];
int c2 = skill[i][4];
int val = skill[i][5];
if (skill[i][0] == 1) { //적공격
query[r1][c1] -= val;
if(c2+1 < m) query[r1][c2 + 1] += val;
if(r2+1 < n) query[r2 + 1][c1] += val;
if(r2+1 < n && c2+1<m) query[r2 + 1][c2 + 1] -= val;
} else {
query[r1][c1] += val;
if(c2+1 < m)query[r1][c2 + 1] -= val;
if(r2+1 < n)query[r2 + 1][c1] -= val;
if(r2+1 < n && c2+1<m)query[r2 + 1][c2 + 1] += val;
}
}
//prefixSum
for (int i = 0; i < query.length; i++) {
for (int j = 1; j < query[i].length; j++) {
query[i][j] += query[i][j - 1];
}
}
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
query[j][i] += query[j-1][i];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
board[i][j] += query[i][j];
if(board[i][j] > 0) answer++;
}
}
return answer;
}
public static void main(String[] args) throws IOException {
Main T = new Main();
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int[][] board = {{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5}};
int[][] skill = {{1, 0, 0, 3, 4, 4}, {1, 2, 0, 2, 3, 2}, {2, 1, 0, 3, 1, 2}, {1, 0, 1, 3, 3, 1}};
T.solution(board, skill);
}
}