📌 배열
✅ Array(배열)의 형태
- 메모리 상에 데이터(원소)를 연속하게 배치한 자료구조 이다.
- 배열의 종류에는 직선형(1차원 배열), 직사각형형(2차원 배열), 직육면체형(3차원 배열) 등이 있다.

✅ Array(배열)의 특징
- 추가적으로 소모되는 메모리 양(=overhead)이 거의 없다.
- Cache hit rate가 높다.
- 배열을 생성하려면 메모리 상에 연속한 구간을 할당해야 해서 할당에 제약이 걸릴 수 있다.
✅ Array(배열)에서 사용할 수 있는 연산들과 시간복잡도
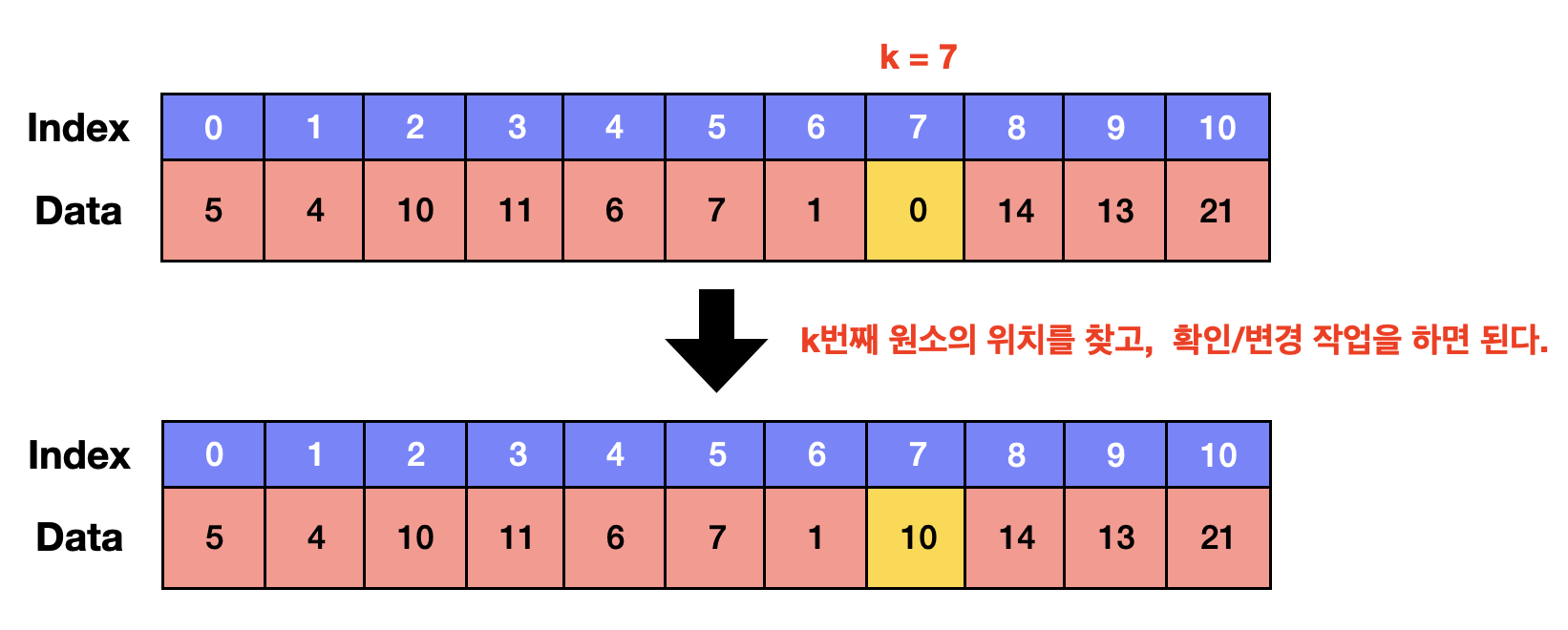
✔ 임의의 위치에 있는 원소를 확인하거나 변경하는 연산 : O(1)의 시간이 걸림
메모리 상에 일렬로 나열되어 있으니 배열의 시작 주소에서 k칸 만큼 더하면 k번째 원소를 찾을 수 있다.
k번째 원소의 위치 = 시작주소 + (1칸이 차지하는 주소 X k)
이므로 단순 사칙연산 계산에 의해 O(1)만에 k번째 원소를 찾을 수 있다.
k번째 원소 위치를 찾았다면 원소를 확인하거나 변경해주면 된다.
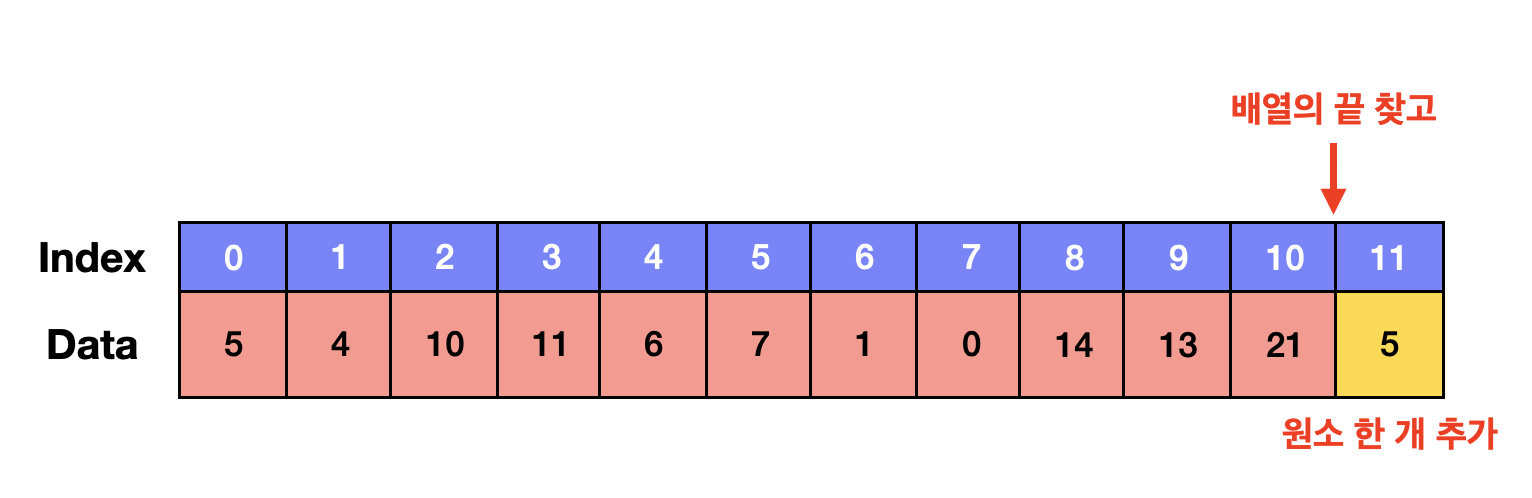
✔ 배열의 가장 끝에 원소 추가하기 : O(1)의 시간이 걸림
배열의 끝 주소 = 시작 주소 + (1칸이 차지하는 주소 X 배열 길이)
위 수식을 통해 배열의 끝 주소를 찾고, 배열의 길이를 1 증가시킨 후, 추가할 원소 데이터를 저장하면 된다.
이것도 시간복잡도는 O(1)이다.
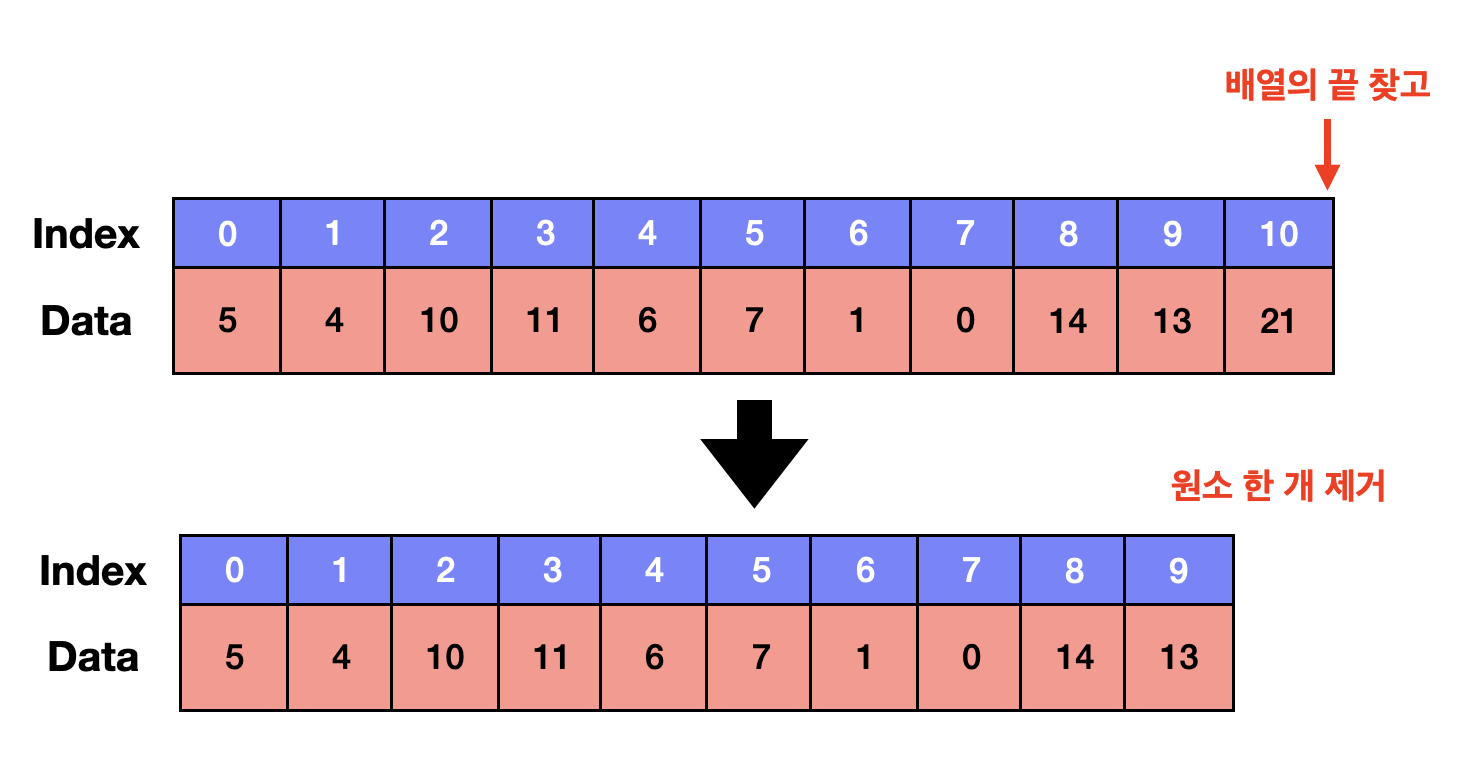
✔ 배열의 가장 끝 원소 삭제하기 : O(1)의 시간이 걸림
위에서 알아본 배열의 가장 끝에 원소 추가하기와 비슷하게 배열의 끝 주소를 찾고, 배열의 길이를 1만큼 줄이면 되므로 시간복잡도는 O(1)이다.
✔ 임의의 위치에 원소를 추가하기 : O(N)의 시간이 걸림
임의의 위치에 원소를 새로 추가해서 끼워넣으려면 그 뒤에 존재하는 모든 원소들을 한 칸씩 뒤로 밀어야 한다.
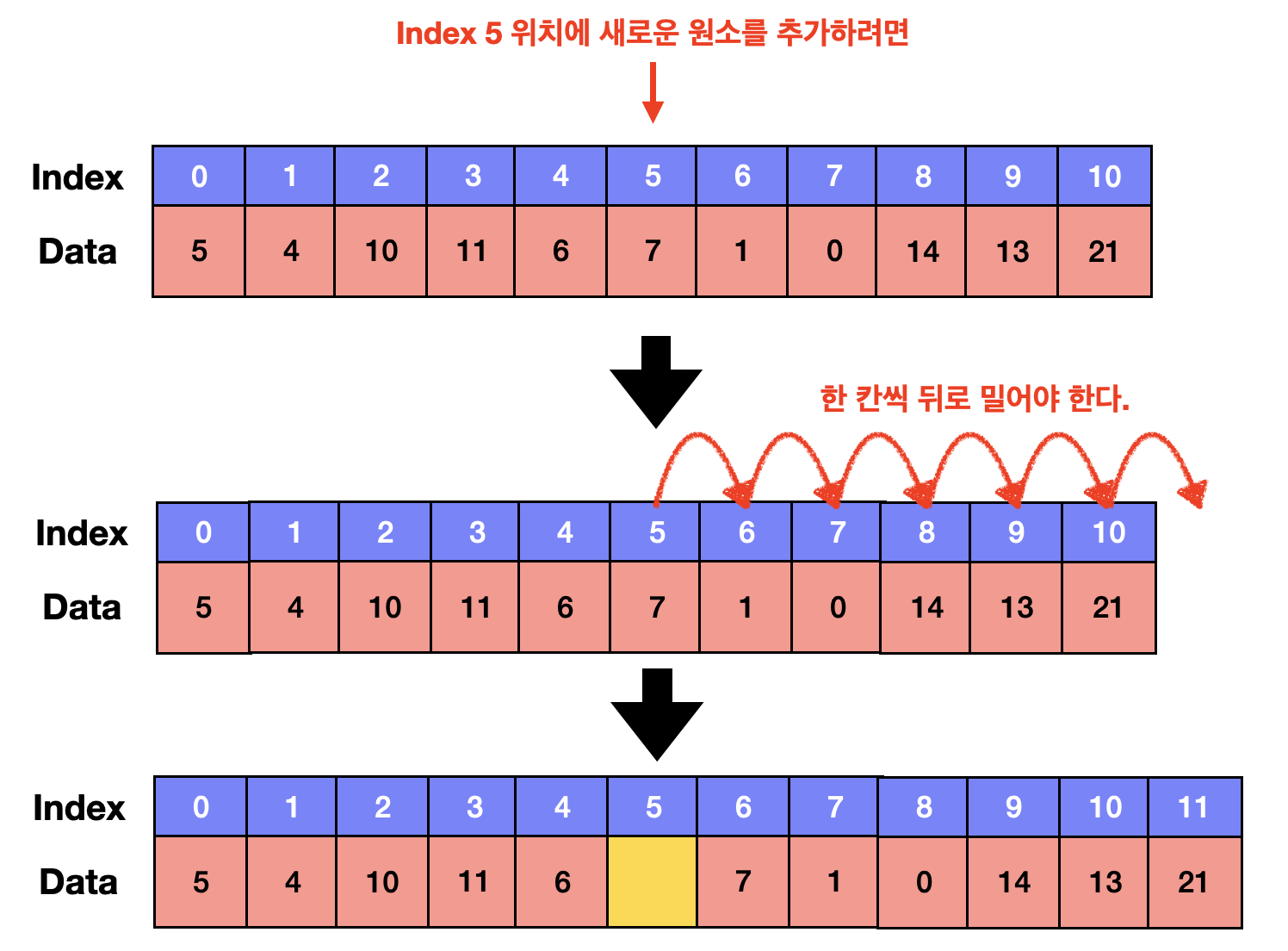
뒤로 미는 연산이 한 번 일어날 때 O(1)이 걸린다. 만약 N개의 원소를 한 칸씩 밀어야 한다면 O(1XN) = O(N)이 걸리게 된다.
추가하려는 위치가 배열의 끝과 가까울수록 그 뒤에 존재하는 원소의 개수가 적어져 뒤로 밀어내는 연산의 수도 줄어든다.
추가하려는 위치가 배열의 처음과 가까울수록 그 뒤에 존재하는 원소의 개수가 많아져 뒤로 밀어내는 연산의 수도 늘어난다.
하지만 평균으로 계산해보면 N/2 개의 원소를 뒤로 밀어내야 하므로 시간복잡도는 O(N/2) = O(N)이 걸린다.
✔ 임의의 위치에 있는 원소를 제거하기 : O(N)의 시간이 걸림
이 연산도 임의의 위치에 원소를 추가하는 것과 비슷하게 수행된다.
임의의 위치에 있는 원소를 삭제하면 그 뒤에 존재하는 모든 원소들을 한 칸씩 앞으로 당겨와야 한다.
왜 굳이 앞으로 당겨와야 할까?
배열의 정의 상 배열은 메모리 상에 데이터(원소)를 연속하게 배치한 자료구조이기 때문이다.
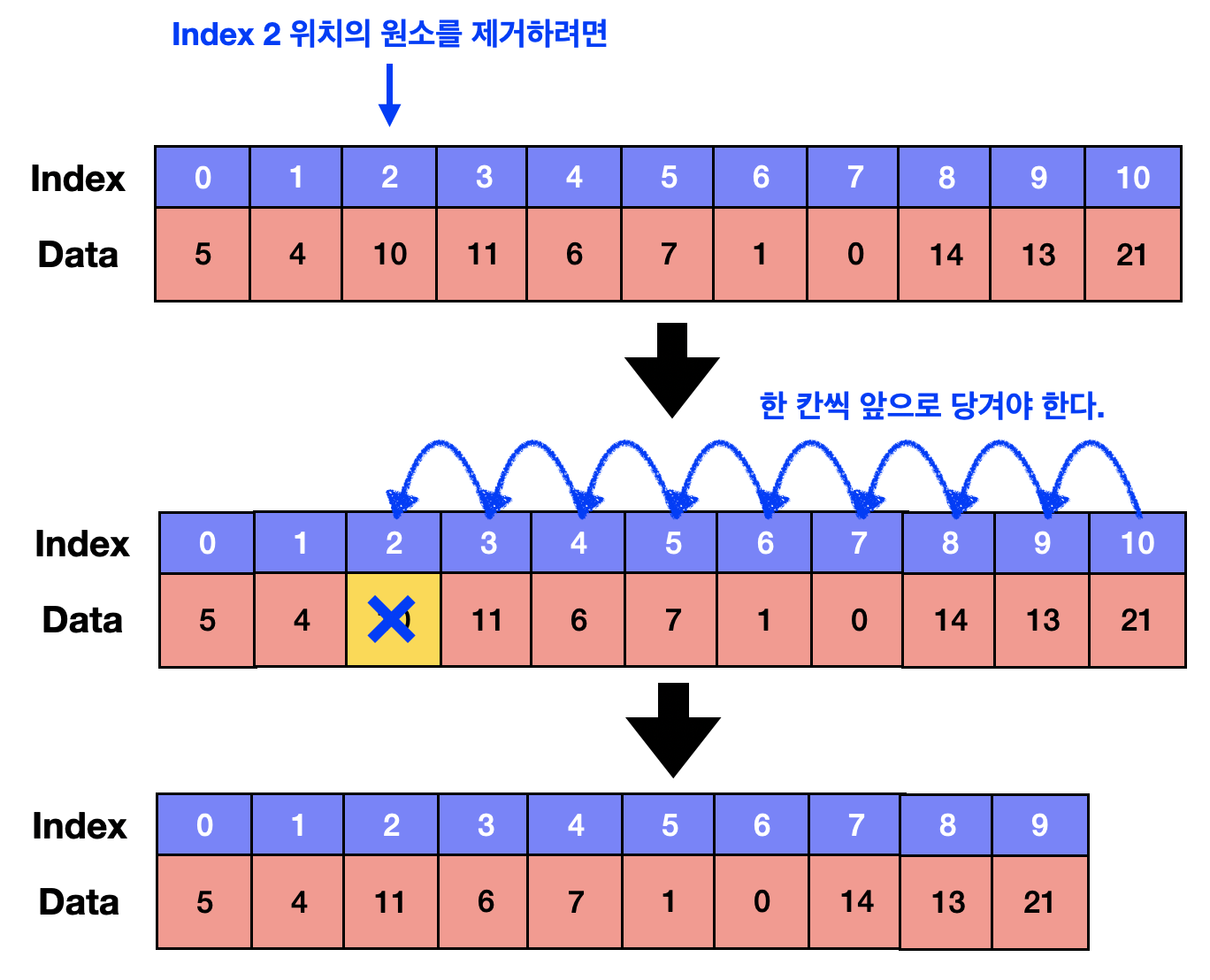
앞으로 당기는 연산이 한 번 일어날 때 O(1)이 걸린다. 만약 N개의 원소를 한 칸씩 앞으로 당겨야 한다면 O(1XN) = O(N)이 걸리게 된다.
제거하려는 원소의 위치가 배열의 끝과 가까울수록 그 뒤에 존재하는 원소의 개수가 적어져 앞으로 당기는 연산의 수도 줄어든다.
제거하려는 위치가 배열의 처음과 가까울수록 그 뒤에 존재하는 원소의 개수가 많아져 앞으로 당기는 연산의 수도 늘어난다.
하지만 평균으로 계산해보면 N/2 개의 원소를 앞으로 당겨야 하므로 시간복잡도는 O(N/2) = O(N)이 걸린다.
✅ Array(배열)의 장/단점
✔ 장점
- Index를 통해 원소에 O(1) 시간복잡도 만에 빠르게 접근할 수 있다.
✔ 단점
-
새로운 원소를 삽입하고 삭제하는데 O(N) 시간복잡도가 걸려 느리다.
-
연속된 메모리 상에 원소들이 존재하므로 처음 배열을 선언한 크기만큼 데이터를 저장하지 않는다면 메모리 낭비가 발생한다.
- 예를 들어, 배열 선언시 배열의 크기를 10으로 선언했는데 3개의 원소에만 데이터를 저장했을 경우 7개의 원소는 비어있게 되므로 7개 원소가 차지하는 메모리 공간만큼 낭비가 발생하게 된다.
✔ 배열을 언제 사용해야 좋을까?
-
데이터 개수가 확실하게 정해져 있을 때 데이터 저장을 위한 자료구조로 선택하면 좋다.
-
또한, 삽입/삭제 작업이 적을 때 사용하면 좋다.
-
마지막으로 배열에 저장된 데이터를 검색하는 작업이 많을 때 사용하면 좋다.(인덱스로 빠르게 검색 가능)