본 게시글에서는 고윳값과 고유벡터를 이용하여 차원축소를 하는 방법인 PCA에 대해서 알아볼 것이다.
차원축소의 목적
데이터의 분산을 최대로 보존하는 축에 정사영하여야 한다.
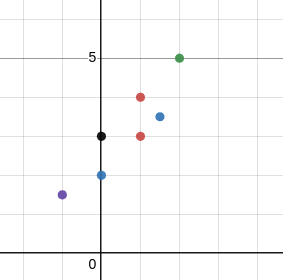
분산을 보존한다는 의미는 무엇일까? 다음과 같은 데이터가 존재하고, y축과 x축, 직선에 정사영해보자.
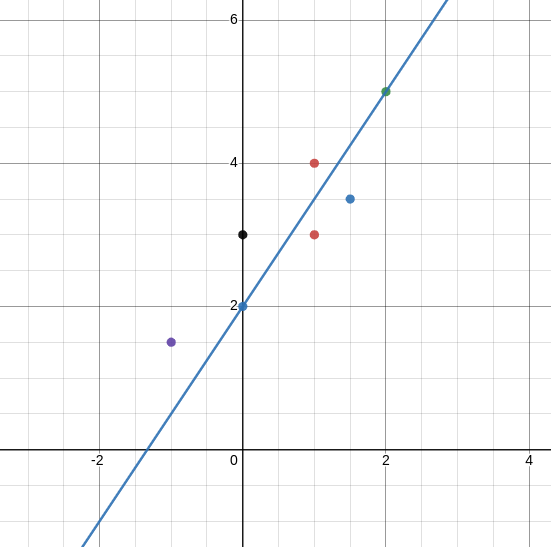
정보가 가장 많이 유지되는 벡터가 분산을 가장 많이 유지하는 벡터이며, 위 사진의 경우에는 직선이 y축과 x축에 비해 정사영하기에 적절해 보인다.
PCA (주성분 분석)
우리의 목적은 데이터의 분산을 최대로 유지하는 벡터들을 찾는 것이다.
그리고 그 벡터에 정사영을 하여 차원축소를 할 수 있다.
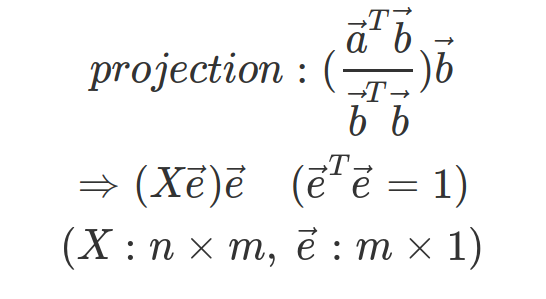
위의 그림과 같이 데이터의 개수가 n개이고, feature의 크기가 m인 경우를 생각해보자.
결과식에서 분산은 X\vec{e}에 따라 결정되므로 다음을 만족하는 벡터 e를 찾는 것이 목적이다.
또한 PCA에서는 데이터의 평균이 0이라는 것과 정사영 벡터의 norm이 1이라는 전제조건이 있다.
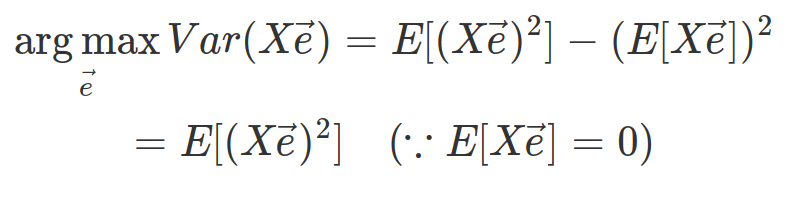
위 식을 좀 더 정리해보면 다음과 같다.
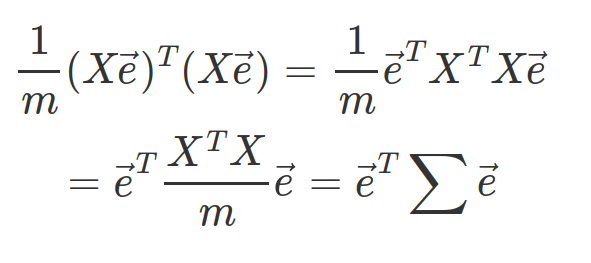
공분한 행렬을 summation 기호로 표현하였다. 공분산 행렬은 m by m 행렬로써, i번째 행 j번째 열의 값은 i번째 feature와 j번째 feature가 얼마나 같이 흩어져 있는지를 의미한다.
정리된 식의 최댓값을 찾기 위해서 라그랑주 승수법을 이용해 볼 것이다.
제약조건을 벡터 e의 norm이 1인 것으로 하고, 보조함수를 작성하여 풀어보면 다음과 같다.
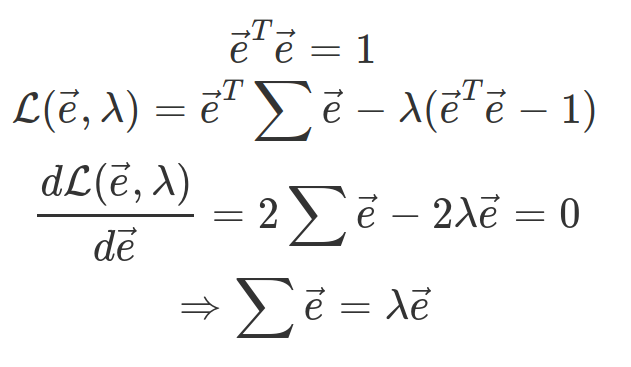
분산을 최대로 하는 정사영 벡터 e는 데이터 행렬 X의 공분산 행렬의 고유벡터이다!
이 결과를 통해 다음과 같은 성질도 찾을 수 있다.
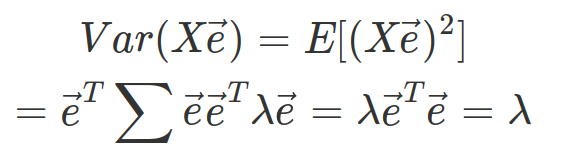
정사영된 결과의 분산은 고윳값이다.
고윳값이 높은 순서대로 정사영을 하여 차원축소를 하는 것이 바람직할 것이다.
PCA와 AutoEncoder
하지만 PCA는 데이터 크기가 증가할수록 연산량이 증가하기 때문에 대량의 데이터셋에서 차원축소를 할 때에는 AutoEncoder를 이용하기도 한다.
둘 다 차원축소 기법이라는 점은 동일하지만, 약간의 차이점이 있다.
PCA: 비교적 작은 데이터 크기, 선형, 초평면 학습
AutoEncoder: 비교적 큰 데이터 크기, 비선형, manifold 학습