[C++] BST (이진 탐색 트리) 구현

BST

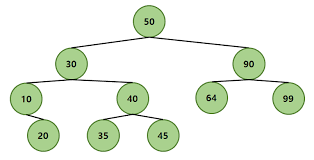
• 이진 탐색 트리는 루트 노드를 기준으로 왼쪽에는 작은 값을, 오른쪽에는 큰 값을 갖는 이진 트리의 한 종류이다.
  모든 노드는 자신을 기준으로 왼쪽 자식값은 자신보다 작고, 오른쪽 자식값은 자신보다 큰 구조를 갖고 있다.

이진 탐색(binary search) ✚ 연결 리스트(linked list)를 결합한 이진트리
이진 탐색의 효율적인 탐색 능력을 유지하면서 빈번한 자료 입력과 삭제를 가능하게끔 고안됨.

특징

• 각 노드에 중복되지 않는 키(Key)가 있다.
• 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.
• 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.
• 좌우 서브트리도 모두 이진 탐색 트리여야 한다.

즉, 이진 탐색 트리(Binary Search Tree)는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가진다.

장점

• 탐색 연산 시간복잡도가 O(log N)이다.

단점

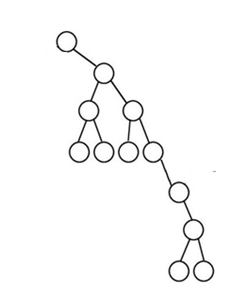
• 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있다. 이렇게 한쪽으로 치우쳐지게 되면 트리 탐색의 장점인 O(log N) 시간복잡도가 마치 배열을 순차탐색 하듯 하는 O(N)에 가까워지게 된다.
  (이러한 문제를 해결하기 위해 고안된 이진 탐색 트리로 AVL 트리, 레드블랙 트리 가 있다.)
• 배열보다 많은 메모리를 사용한다.

코드

#pragma once

#include <assert.h>

enum class NODE_TYPE
{
	PARENT, // 0
	LCHILD, // 1
	RCHILD, // 2
	END,    // 3
};

template<typename T1, typename T2>
struct tPair
{
	T1 first;
	T2 second;
};

template<typename T1, typename T2>
tPair<T1, T2> make_bstpair(const T1& _first, const T2& _second)
{
	return tPair<T1, T2>{ _first, _second };
}


template <typename T1, typename T2>
struct tBSTNode
{
	tPair<T1, T2>	pair;
	tBSTNode<T1,T2>*		arrNode[(int)NODE_TYPE::END];

	bool IsRoot()
	{
		if (nullptr == arrNode[(int)NODE_TYPE::PARENT])
			return true;
		return false;
	}

	bool IsLeftChild()
	{
		if (arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] == this)
			return true;
		return false;
	}

	bool IsRightChild()
	{
		if(arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] == this)
			return true;
		return false;
	}

	bool IsLeaf()
	{
		if (nullptr == arrNode[(int)NODE_TYPE::LCHILD] && nullptr == arrNode[(int)NODE_TYPE::RCHILD])
			return true;
		return false;
	}

	bool IsFull()
	{
		if (arrNode[(int)NODE_TYPE::LCHILD] && arrNode[(int)NODE_TYPE::RCHILD])
			return true;
		return false;
	}

	tBSTNode()
		: pair()
		, arrNode{}
	{}

	tBSTNode(const tPair<T1, T2>& _pair, tBSTNode<T1, T2>* _pParent, tBSTNode<T1, T2>* _pLChild, tBSTNode<T1, T2>* _pRChild)
		: pair(_pair)
		, arrNode{_pParent, _pLChild, _pRChild}
	{}
};


template <typename T1, typename T2>
class CBST
{
private:
	tBSTNode<T1,T2>*	m_pRoot;  // 루트 노드 주소
	int					m_iCount; // 데이터 개수
	
public:
	bool insert(const tPair<T1,T2>& _pair);
	tBSTNode<T1, T2>* GetInOrderSuccessor(tBSTNode<T1, T2>* _pNode);
	tBSTNode<T1, T2>* GetInOrderPredecessor(tBSTNode<T1, T2>* _pNode);
	
	class iterator;
public:
	iterator begin();
	iterator end();
	iterator find(const T1& _find);
	iterator erase(const iterator& _iter);

private:
	tBSTNode<T1, T2>* DeleteNode(tBSTNode<T1, T2>* _pTargetNode);


public:
	CBST()
		: m_pRoot(nullptr)
		, m_iCount(0)
	{}

	// iterator
	class iterator
	{
	private:
		CBST<T1, T2>*		 m_pBST;
		tBSTNode<T1, T2>*	 m_pNode; // null 인 경우 end iterator

	public:
		bool operator == (const iterator& _other)
		{
			if (m_pBST == _other.m_pBST && m_pNode == _other.m_pNode)
				return true;

			return false;
		}

		bool operator !=(const iterator& _other)
		{
			return !(*this == _other);
		}

		const tPair<T1, T2>& operator*()
		{
			// m_pNode nullptr 체크(end iterator 인지 아닌지)
			assert(m_pNode);

			return m_pNode->pair;
		}

		const tPair<T1, T2>* operator->()
		{
			// m_pNode nullptr 체크(end iterator 인지 아닌지)
			assert(m_pNode);

			return &m_pNode->pair;
		}

		iterator& operator ++()
		{
			m_pNode = m_pBST->GetInOrderSuccessor(m_pNode);
			
			return *this;
		}

		
	public:
		iterator()
			: m_pBST(nullptr)
			, m_pNode(nullptr)
		{}

		iterator(CBST<T1, T2>* _pBST, tBSTNode<T1, T2>* _pNode)
			: m_pBST(_pBST)
			, m_pNode(_pNode)
		{}

		friend class CBST<T1, T2>;
	};
};



template<typename T1, typename T2>
inline bool CBST<T1, T2>::insert(const tPair<T1, T2>& _pair)
{
	tBSTNode<T1, T2>* pNewNode = new tBSTNode<T1, T2>(_pair, nullptr, nullptr, nullptr);

	// 첫번째 데이터 라면
	if (nullptr == m_pRoot)
	{
		m_pRoot = pNewNode;
	}
	else
	{
		tBSTNode<T1, T2>* pNode = m_pRoot; // m_pRoot 를 훼손시키지 않기 위해
		NODE_TYPE node_type = NODE_TYPE::END;

		while (true)
		{
			if (pNode->pair.first < pNewNode->pair.first)
				node_type = NODE_TYPE::RCHILD;
			else if (pNode->pair.first > pNewNode->pair.first)
				node_type = NODE_TYPE::LCHILD;
			else
			{
				cout << "중복된 키 값이 있습니다" << endl;
				return false;
			}

			if (nullptr == pNode->arrNode[(int)node_type])
			{
				pNode->arrNode[(int)node_type] = pNewNode;
				pNewNode->arrNode[(int)NODE_TYPE::PARENT] = pNode;
				break;
			}
			else
			{
				pNode = pNode->arrNode[(int)node_type];
			}
		}
	}

	// 데이터 개수 증가
	++m_iCount;

	return true;
}

template<typename T1, typename T2>
inline tBSTNode<T1, T2>* CBST<T1, T2>::GetInOrderSuccessor(tBSTNode<T1, T2>* _pNode)
{
	tBSTNode<T1, T2>* pSuccessor = nullptr;

	// 1. 오른쪽 자식이 있는 경우, 오른쪽 자식으로 가서, 왼쪽 자식이 없을 때 까지 내려감
	if (nullptr != _pNode->arrNode[(int)NODE_TYPE::RCHILD])
	{
		pSuccessor = _pNode->arrNode[(int)NODE_TYPE::RCHILD];

		while (pSuccessor->arrNode[(int)NODE_TYPE::LCHILD])
		{
			pSuccessor = pSuccessor->arrNode[(int)NODE_TYPE::LCHILD];
		}
	}

	// 2. 부모로 부터 왼쪽 자식일 때 까지 위로 올라감, 그 때 부모가 후속자
	else
	{
		pSuccessor = _pNode;

		while (true)
		{ 
			// 더 이상 위쪽으로 올라갈 수 없다. ==> 마지막 노드
			if (pSuccessor->IsRoot())
				return nullptr;

			// 부모로 부터 왼쪽 자식인지 체크
			if (pSuccessor->IsLeftChild())
			{
				// 그때 부모가 후속자
				pSuccessor = pSuccessor->arrNode[(int)NODE_TYPE::PARENT];
				break;
			}

			// 아니라면 부모로 부터 오른쪽 자식이니까 부모로 올라감
			else
				pSuccessor = pSuccessor->arrNode[(int)NODE_TYPE::PARENT];
		}
	}

	return pSuccessor;
}

template<typename T1, typename T2>
inline tBSTNode<T1, T2>* CBST<T1, T2>::GetInOrderPredecessor(tBSTNode<T1, T2>* _pNode)
{
	tBSTNode<T1, T2>* pSuccessor = nullptr;

	// 1. 왼쪽 자식이 있는 경우, 왼쪽 자식으로 가서, 오른쪽 자식이 없을 때 까지 내려감
	if (nullptr != _pNode->arrNode[(int)NODE_TYPE::LCHILD])
	{
		pSuccessor = _pNode->arrNode[(int)NODE_TYPE::LCHILD];

		while (pSuccessor->arrNode[(int)NODE_TYPE::RCHILD])
		{
			pSuccessor = pSuccessor->arrNode[(int)NODE_TYPE::RCHILD];
		}
	}

	// 2. 부모로 부터 오른쪽 자식일 때 까지 위로 올라감, 그 때 부모가 후속자
	else
	{
		pSuccessor = _pNode;

		while (true)
		{
			// 더 이상 위쪽으로 올라갈 수 없다. ==> 마지막 노드
			if (pSuccessor->IsRoot())
				return nullptr;

			// 부모로 부터 오른쪽 자식인지 체크
			if (pSuccessor->IsRightChild())
			{
				// 그때 부모가 후속자
				pSuccessor = pSuccessor->arrNode[(int)NODE_TYPE::PARENT];
				break;
			}

			// 아니라면 부모로 부터 왼쪽 자식이니까 부모로 올라감
			else
				pSuccessor = pSuccessor->arrNode[(int)NODE_TYPE::PARENT];
		}
	}


	return pSuccessor;
}

template<typename T1, typename T2>
inline typename CBST<T1,T2>::iterator CBST<T1, T2>::begin()
{
	tBSTNode<T1,T2>* pNode = m_pRoot;

	while (pNode->arrNode[(int)NODE_TYPE::LCHILD])
	{
		pNode = pNode->arrNode[(int)NODE_TYPE::LCHILD];
	}

	return iterator(this, pNode);
}

template<typename T1, typename T2>
inline typename CBST<T1, T2>::iterator CBST<T1, T2>::end()
{
	return iterator(this, nullptr);
}

template<typename T1, typename T2>
inline typename CBST<T1, T2>::iterator CBST<T1, T2>::find(const T1& _find)
{
	tBSTNode<T1, T2>* pNode = m_pRoot; // m_pRoot 를 훼손시키지 않기 위해
	NODE_TYPE node_type = NODE_TYPE::END;

	while (true)
	{
		if (pNode->pair.first < _find)
			node_type = NODE_TYPE::RCHILD;
		else if (pNode->pair.first > _find)
			node_type = NODE_TYPE::LCHILD;
		else
		{
			// pNode 가 현재 찾으려는 노드다.
			break;
		}

		if (nullptr == pNode->arrNode[(int)node_type])
		{
			// pNode = nullptr ==> end iterator
			pNode = nullptr;
			break;
		}
		else
		{
			pNode = pNode->arrNode[(int)node_type];
		}
	}

	return iterator(this, pNode);
}

template<typename T1, typename T2>
inline typename CBST<T1,T2>::iterator CBST<T1, T2>::erase(const iterator& _iter)
{
	assert(this == _iter.m_pBST);

	tBSTNode<T1,T2>* pSuccessor = DeleteNode(_iter.m_pNode);

	return iterator(this, pSuccessor);
}

template<typename T1, typename T2>
inline tBSTNode<T1, T2>* CBST<T1, T2>::DeleteNode(tBSTNode<T1, T2>* _pTargetNode)
{
	// 삭제시킬 노드의 후속자 노드를 찾아둔다.
	tBSTNode<T1, T2>* pSuccessor = GetInOrderSuccessor(_pTargetNode);

	// 1. 자식이 하나도 없는 경우
	if (_pTargetNode->IsLeaf())
	{
		// 삭제할 노드가 루트였다. (자식이 없고 루트 ==> BST 안에 데이터가 1개밖에 없었다.)
		if (_pTargetNode == m_pRoot)
		{
			m_pRoot = nullptr;
		}
		
		else
		{
			// 부모노드로 접근해서 삭제될 노드인 자식을 가리키는 포인터를 nullptr 로 만든다.
			if (_pTargetNode->IsLeftChild())
				_pTargetNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = nullptr;
			else
				_pTargetNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = nullptr;
		}

		delete _pTargetNode;

		// 데이터 개수 맞춰줌  
		--m_iCount;
	}

	// 2. 자식이 2개인 경우
	else if (_pTargetNode->IsFull())
	{
		// 삭제 될 자리에 중위 후속자의 값을 복사시킨다.
		_pTargetNode->pair = pSuccessor->pair;

		// 중위 후속자 노드를 삭제한다.
		DeleteNode(pSuccessor);

		// 삭제할 노드가 중위 후속자가 되었다.
		pSuccessor = _pTargetNode;
	}

	// 3. 자식이 1개인 경우
	else
	{
		NODE_TYPE eChildType = NODE_TYPE::LCHILD;
		if (_pTargetNode->arrNode[(int)NODE_TYPE::RCHILD])
			eChildType = NODE_TYPE::RCHILD;

		// 삭제할 노드가 루트였다.
		if (_pTargetNode == m_pRoot)
		{
			// 자식 노드(1개)를 루트로 만든다.
			m_pRoot = _pTargetNode->arrNode[(int)eChildType];

			// 루트로 만들 자식노드의 부모를 nullptr 로 만든다.
			_pTargetNode->arrNode[(int)eChildType]->arrNode[(int)NODE_TYPE::PARENT] = nullptr;
		}

		else
		{
			// 삭제될 노드의 부모와, 삭제될 노드의 자식을 연결해준다.
			if (_pTargetNode->IsLeftChild())
			{
				_pTargetNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = _pTargetNode->arrNode[(int)eChildType];
			}

			else
			{
				_pTargetNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = _pTargetNode->arrNode[(int)eChildType];
			}

			_pTargetNode->arrNode[(int)eChildType]->arrNode[(int)NODE_TYPE::PARENT] = _pTargetNode->arrNode[(int)NODE_TYPE::PARENT];
		}
		
		delete _pTargetNode;

		// 데이터 개수 맞춰줌
		--m_iCount;
	}

	
	// --m_iCount; 이곳에 두게되면 자식이 2개인 경우에서는 m_iCount 가 2번 빼지기 때문에 1, 3번 케이스에서만 빼게끔 한다.

	return pSuccessor;
}

삽입, 탐색, 삭제
*, ->, begin, end, , iterator, ++, --, ==, != 들을 구현했다.

삭제시킬 노드의 후속자로 중위선행자와 중위후속자 중에서 후속자로 선택했다.

정리

enum, enum class 에 대해서 배웠고, IsRoot, IsLeaf 등등 작은 기능들을 만들어두고 사용하면 코드가 클린해지고 간편해지는걸 느꼈다.

vector 와 list 에 이어서 BTS 를 강의 영상을 보면서 해보았는데 세 가지 전부 해보면서 느꼈지만, 순간순간은 이해가 되는데 전체적으로 보게 되면 막막해진다.
열심히 복습하고 끈기 있게 하나하나 풀어나가야겠다.

C/C++ 강의 69화. tree (1)
[자료구조] 이진 트리와 이진 탐색 트리 (BST: Binary Search Tree)
[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현