Binary search tree (BST)

이진 검색 트리를 살펴보기 전에 트리와 이진 트리가 무엇인지부터 알아보자.

Tree

일단 앞써 살펴봤던 그래프와 트리의 차이점을 정리해 놓은 표를 참고하면 이해하기 쉽다.

트리는 방향 그래프 (부모 => 자식) 이고 비순환 그래프이다.
또 그래프와 가장 큰 차이점은 정점 노드가 있는다는 것이다.
그래프는 네트워크 모델이며 트리는 부모 자식관계가 있는 계층 모델이다.
정점의 수가 n개이면 n -1의 간선을 가진다.

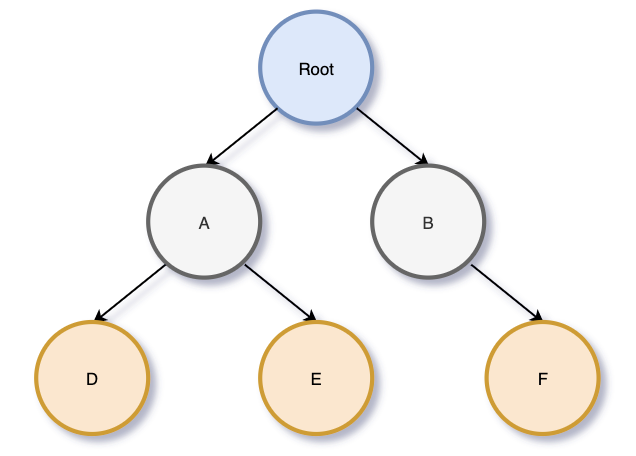
여기서 자식의 수가 항상 2보다 작거나 같은 트리를 이진 트리라고 한다.

여기서 더 나아가 일정한 규칙으로 뻗어나가며 순서가 있는 데이터 구조로 정리한다면 (예: 왼쪽은 작은 숫자 오른쪽은 큰 숫자) 이진 검색 트리라고도 한다.
순서가 있는 데이터들을 찾고 넣을 일이 많을 때 BST를 사용한다.

트리가 Unbalance하게 한쪽으로 치우쳐진다면 검색, 삭제, 삽입에서 O(n)의 시간 복잡도를 갖지만 balance가 잘 맞춰져있다면 O(log n)의 시간 복잡도를 갖는다.

그렇다면 직접 이진 검색 트리를 구현해보자.

class BST {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }

  insert(value) {
    const newVertex = new BST(value);

    const recursion = vertex => {
      if (vertex.value >= newVertex.value) {
        if (!vertex.left) {
          vertex.left = newVertex;
        } else {
          recursion(vertex.left);
        }
      } else {
        if (!vertex.right) {
          vertex.right = newVertex;
        } else {
          recursion(vertex.right);
        }
      }
    };

    recursion(this);
  }
}

const bsTree = new BST(15);

bsTree.insert(6);
bsTree.insert(23);
bsTree.insert(3);
bsTree.insert(9);
bsTree.insert(19);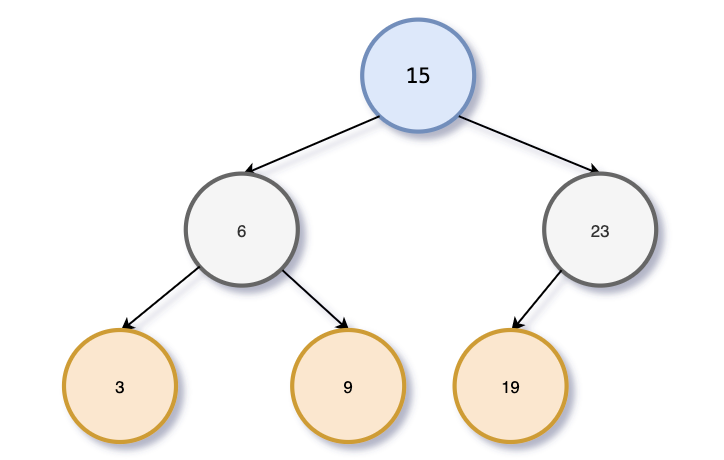

정점이 있는지 확인

contains(value) {
  let result = false;

  if (this.value === value) return true;

  const recursion = vertex => {
    if (vertex.value > value) {
      if (vertex.left.value === value) {
        result = true;
      } else {
        vertex.left && recursion(vertex.left);
      }
    } else {
      if (vertex.value === value) {
        result = true;
      } else {
        vertex.right && recursion(vertex.right);
      }
    }
  };
  recursion(this);
  return result;
}
console.log(bsTree.contains(10)); // false
console.log(bsTree.contains(6)); // true
console.log(bsTree.contains(19)); // true
console.log(bsTree.contains(9)); // true