Graph
그래프를 사용하면 객체 간의 연결을 다양하게 나타낼 수 있다.
그래프는 객체 간의 연결을 시각적으로 표현한 것이다. 실생활의 많은 부분을 그래프로 적용해볼 수 있다.
| 사례 | 항목 | 연결 |
|---|---|---|
| 웹사이트 | 웹 페이지 | 링크 |
| 지도 | 교차로 | 도로 |
| 회로 | 부품 | 배선 |
| 소셜미디어 | 사람 | 친구 또는 팔로우 |
그래프 기본 용어와 개념
-
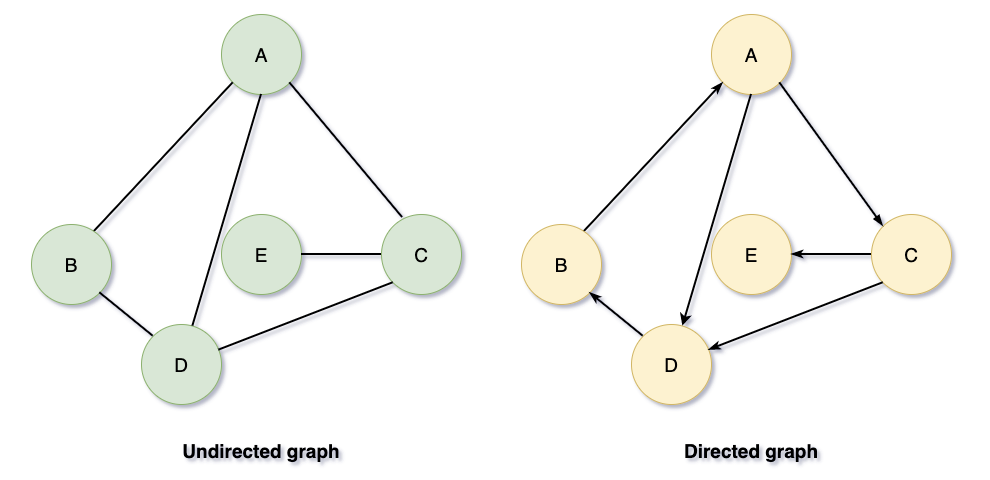
정점(Vertex) : 그래프를 형성하는 노드를 뜻한다. 위의 그림에서 원이 정점을 보여준다.
-
간선(Edge) : 그래프에서 노드 간의 연결을 뜻한다. 그림에서 원(정점)을 이어주는 선이 간선을 나타낸다.
-
정점 차수 : 해당 정점에 연결된 간선의 개수를 나타낸다.
(Ex : 왼쪽 그래프에서 A 정점 차수는 3이다.) -
희소 그래프 : 정점들 간에 가능한 연결 중 일부만 존재하는 경우
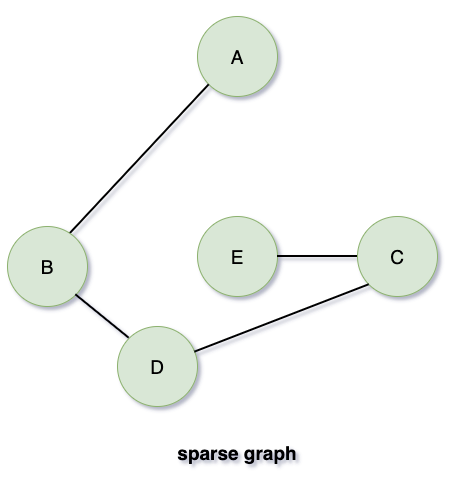
- 밀집 그래프 : 다양한 정점들 간에 연결이 많은 경우
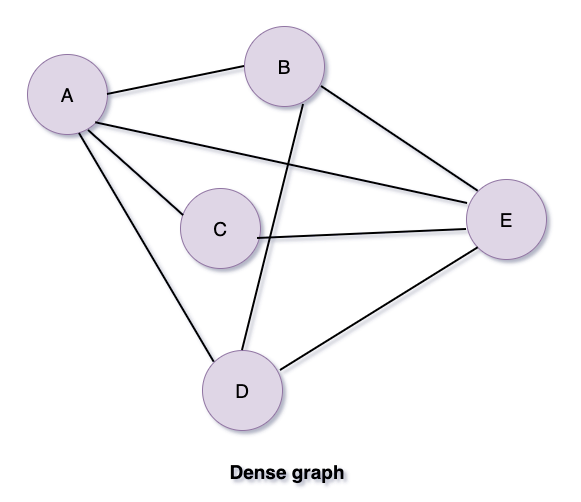
- 순환 & 비순환 그래프 : 어떤 정점에서 출발해 해당 점점으로 다시 돌아오는 경로가 존재하는 지향성 그래프를 말한다. 반대로 비순환 그래프가 있다.
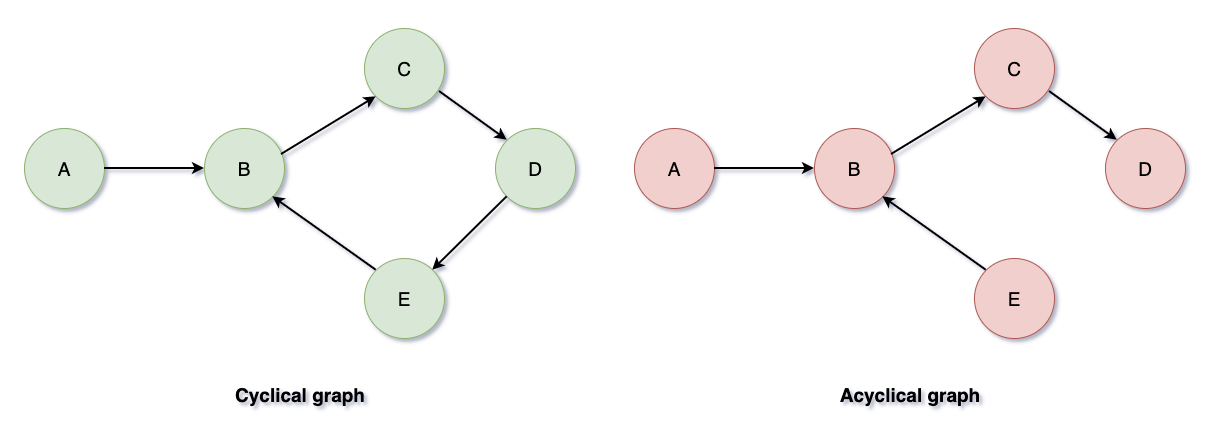
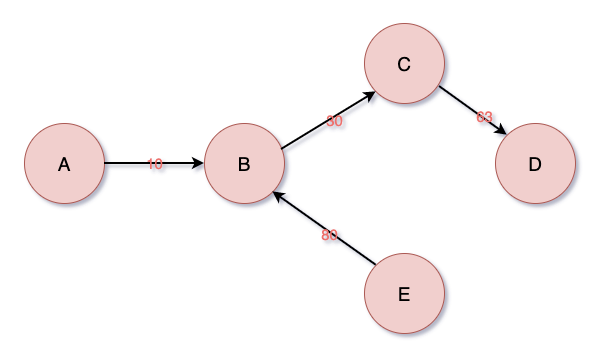
- 가중치 : 간선에 대한 값으로, 문맥에 따라 다양한 것을 나타낼 수 있다.
무지향성 그래프
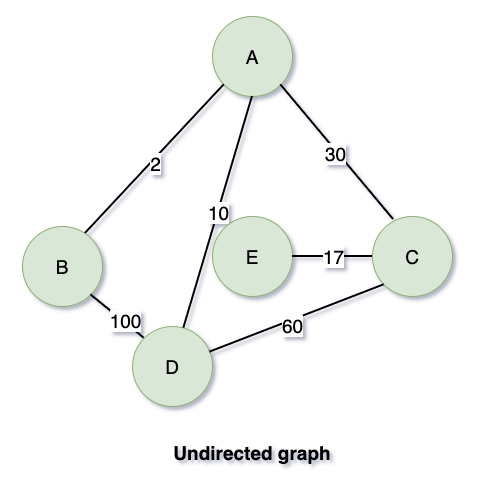
간선 간에 방향이 없는 그래프다. 간선은 두 정점 간에 방향 없이 상호 연결을 암시한다.
실생활 예로 친구 관계를 생각하면 된다. 서로가 친구임을 인정해야 진정한 친구 관계이다.
가중치로는 그 둘이 얼마나 친한지 표현할 수 있겠다.
무지향성 그래프를 자료 구조 클래스로 표현하는 방법에 2가지 인접 행렬, 인접 리스트가 있다.
인접 행렬
행렬의 각 항목이 두 정점 간에 두 정점 간에 연결을 나타내는 V * V 행렬이다.
간선이 있으면 1 없으면 0으로 표기한다. 위의 그래프를 인접 행렬로 나타내면 아래와 같다.
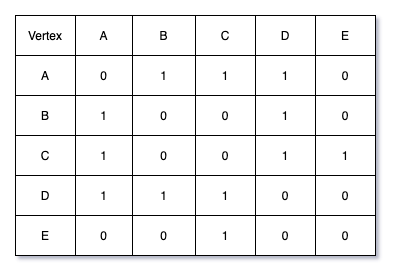
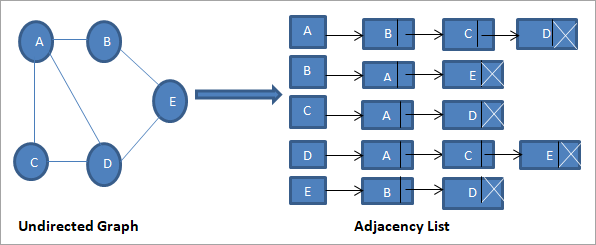
인접 리스트
인접 리스트는 정점을 노드의 키로 사용하며 해당 노드의 이웃들을 리스트에 저장한다.
- 인접 리스트 이미지 출처
간선과 정점 추가
가중치가 있는 무지향성 그래프를 생성하고 정점과 간선을 추가해보자.
class UndirectedGraph {
constructor() {
// 간선을 저장하기 위한 객체.
this.edges = {};
}
addVertex(vertex) {
// 정점들을 간선 값들을 저장하는 this.edges 객체 내에 객체 형태로 저장.
this.edges[vertex] = {};
}
addEdge(vertex1, vertex2, weight = 0) {
// 가중치가 있는 간선을 추가해주기 위해 this.edges 객체의 양쪽 정점에 가중치를 저장.
this.edges[vertex1][vertex2] = weight;
this.edges[vertex2][vertex1] = weight;
}
}
const graph1 = new UndirectedGraph();
graph1.addVertex("철수");
graph1.addVertex("영희");
graph1.addEdge("철수", "영희", "친구");
graph1.addVertex("민지");
graph1.addVertex("동건");
graph1.addVertex("소희");
graph1.addEdge("영희", "민지", "친구");
graph1.addEdge("민지", "동건", "단짝 친구");
graph1.addEdge("소희", "철수", "친구");
console.log(graph1.edges);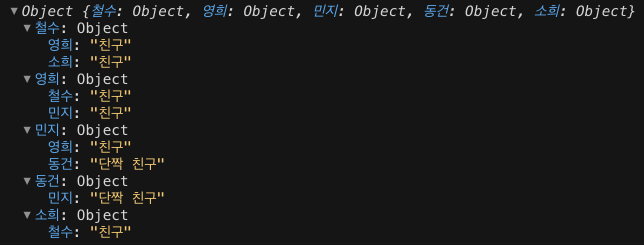
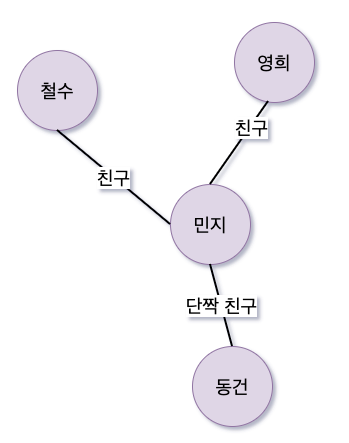
그래프를 그림으로 표현해보면 다음과 같다.
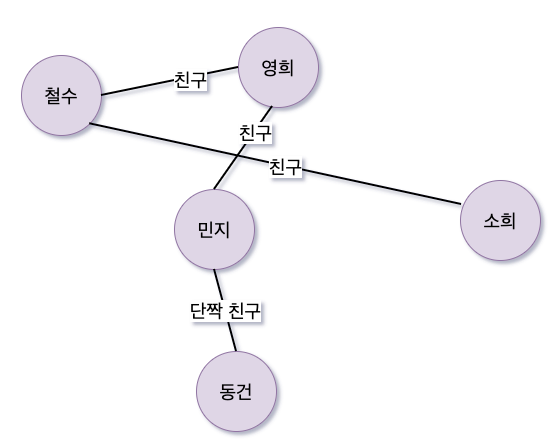
간선과 정점 삭제하기
위의 친구 관계를 나타내는 그래프에서 철수가 영희와 절교 (정점 삭제)를 하고 민지와 새롭게 친구를 한다면 아래와 같다.
// 코드 생략...
// edges 객체에 vertex1 객체에 vertex2가 있는지 확인하고 있다면 delete.
// edges 객체에 vertex2 객체에 vertex1이 있는지 확인하고 있다면 delete.
removeEdge(vertex1, vertex2) {
if (this.edges[vertex1][vertex2]) delete this.edges[vertex1][vertex2];
if (this.edges[vertex2][vertex1]) delete this.edges[vertex2][vertex1];
}
// 코드 생략...
graph1.removeEdge("철수", "영희");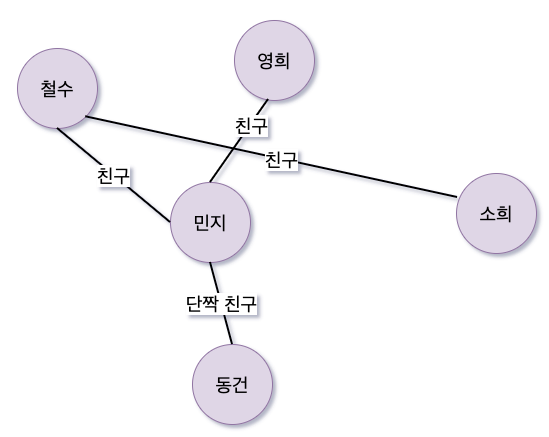
이번에는 소희가 유학을 가버리는 상황 (정점 삭제) 을 가정해보자
// 코드 생략...
// 해당 vertext의 프로퍼티 하나씩 순회하면서 removeEdge 메서드로 edge 삭제.
// 해당 vertex의 edge 삭제.
removeVertex(vertex) {
for (let adjacentVertex in this.edges[vertex]) {
this.removeEdge(adjacentVertex, vertex);
}
delete this.edges[vertex];
}
// 코드 생략...
graph1.removeVertex("소희");철수의 친구 소희는 사라져버렸고 시간이 흘러 그 둘은 서로를 잊어버렸다.
다음 글에서 지향성 그래프에 대해서 정리해보겠다..!
