Hash Table
해시 테이블은 평균 상수시간(O(1))안에 데이터의 삽입, 삭제, 탐색 연산을 제공하는 자료구조이다.
파이썬의 경우 딕셔너리가 해시테이블의 자료구조와 같다.
딕셔너리는 key와 value의 쌍으로 데이터를 저장하는 구조이다.
dic = {}
dic = {"name":"kim", "age":10, "is_developer":True}
중괄호를 이용해서 딕셔너리를 사용할 수 있다.
딕셔너리의 키값은 다른 값들과 구별하기 위한 것으로 모두 다른 값을 가져야 한다.
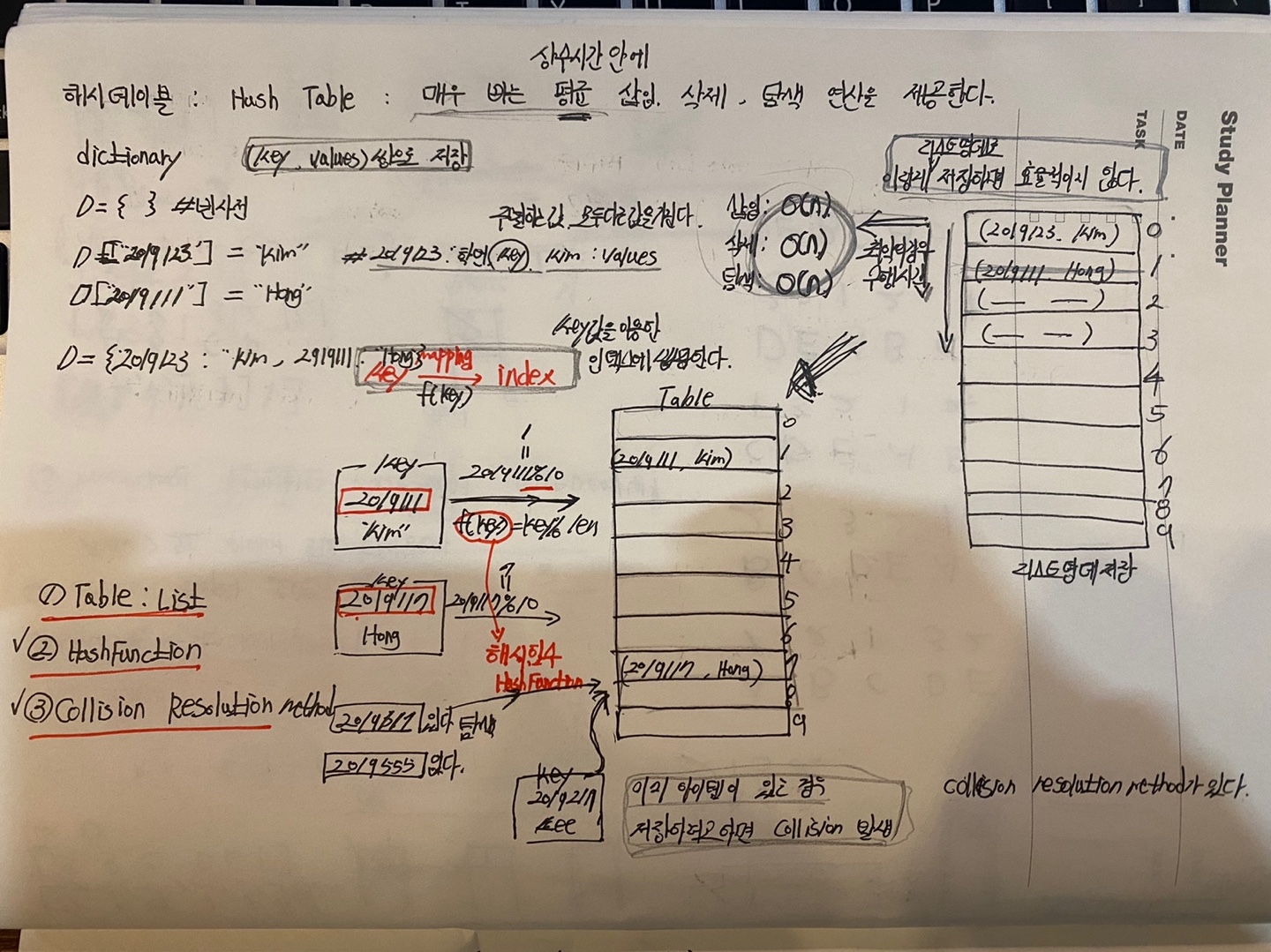
해시테이블은 리스트를 이용해서 구현할 수 있다.
단순히 리스트를 이용해서 키와 벨류를 순차적으로 저장할 시 시간 복잡도의 평균시간은 O(n)이 된다.
삽입시는 맨 마지막 데이터가 저장된 위치까지 이동 후 삽입 해야 하기 때문에
최악의 경우 n만큼 이동해야한다. 탐색시도 마찬가지이다.
삭제의 경우라면 탐색을 하는데도 O(n)이 걸리고, 삭제 후 해당 인덱스의 오른쪽에 있는 모든 요소들을 왼쪽으로 한칸씩 당겨야 하기 때문에 역시 최악의 경우 O(n)이 걸리게된다. 리스트에 순차적으로 데이터를 저장하는 것은 배열과 같다. 해시테이블은 위와 같은 방식으로 데이터를 저장하지 않는다.
해시테이블은 해시함수를 이용해서 리스트안에 저장될 인덱스를 계산 뒤 해당 인덱스에 데이터를 저장한다.
즉, key값을 이용해서 해시함수를 계산 뒤 해당 인덱스에 데이터를 맵핑한다.
리스트내의 인덱스에 키값으로 계산 해시함수를 계산해서 맵핑하기 때문에 배열과 같이 순차적으로 데이터가 저장되는 구조가 아니다.
하지만, 만약 해시함수로 계산한 값이 중복되는 경우라면 어떻게 될까?
키값으 다르지만, 해시함수로 계산한 인덱스가 같은 경우라면, 이미 데이터가 저장되어 있기 때문에 Collision(충돌)이 발생하게 된다.
그렇기 때문에 해시함수에서는 반드시 Collision이 발생했을 때의 Collision Resolution Method를 고려해야한다.
또한 "어떻게 해시함수를 구현할 것인가?" 역시 Collision을 줄일 수 있는 방법 중 하나이다.
Hash Function

좋은 Hash Function이란 무엇인가?
위의 사진에서는 key값을 Hashtable의 Slot 개수로 나누어서 인덱스를 계산 후 데이터를 해당 인덱스에 저장했다.
이러한 방식을 Division Hashfunction이라고 한다.
하지만 Division Hashfunction은 구현 하기는 쉽지만 충돌이 많이 발생한다.
가장 이상적인 해시함수는 slot과 key가 1대1로 맵핑이 되는
Perfect Hash Function의 경우이다.
1대1로 맵핑이 이루어지게 되면 충돌이 발생하지 않는다.
하지만 현실에서는 비현실적인 해시함수이다.
이외에도 위의 사진에 쓰여진 다양한 해시함수가 존재한다.
결국 좋은 해시함수란 Less Collision(적은 충돌), Fast Compution(빠른 계산)이 이루어지는 함수이다.
하지만 두개의 조건은 서로 트레이드오프 관계에 있기 때문에 적절한 균형이 맞는 선에서 Hash Function을 구현하는 것이 좋은 Hash Function이라고 할 수 있다.
충돌회피 방법 - Open Addressing
HashTable에서 Collision은 반드시 발생하는 문제이다. Collision이 발생하지 않는 경우라면 인덱스와 key가 1대1로 맵핑되는 경우뿐인데, 이는 현실에서는 비현실적인 방식이다. 그렇기 때문에 충돌회피방법에 대해서 고려해야한다.
- open addressing
- chaining
위의 2가지가 충돌회피방법들 중 대표적인 것이다.
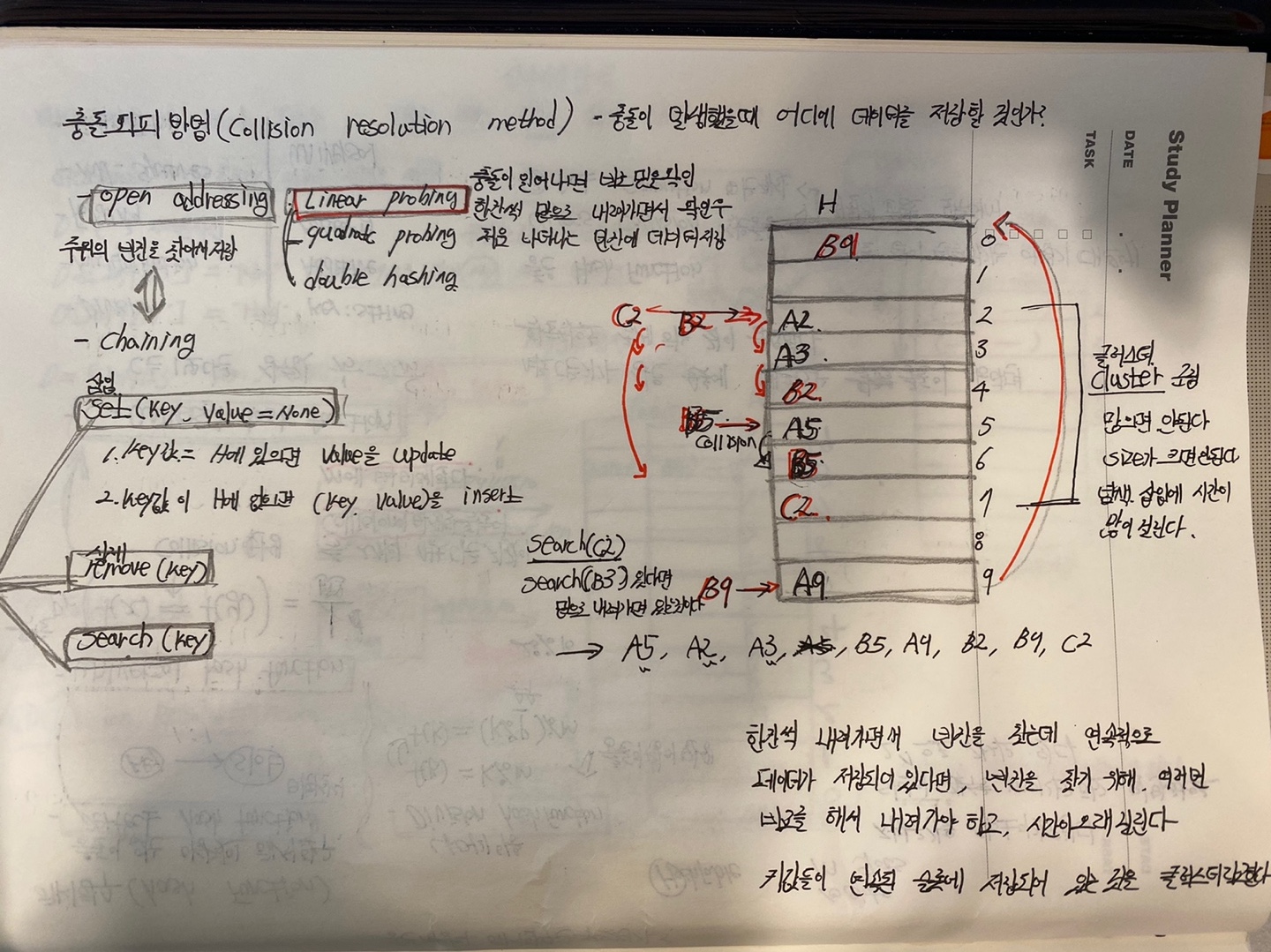
위의 사진에서 설명은 open addressing의 Liner probing기법이다.
Liner probing기법은 충돌이 발생하면 바로 밑을 확인 후 비어있다면, 해당 데이터를 저장, 아니라면 빈칸을 찾을 때까지 밑으로 이동하는 것을 말한다.
이렇게 Liner probing기법을 이용해서 Collision을 해결하게 되면, Cluster(클러스터)가 발생하게 된다.
클러스터는 빈칸을 찾아서 밑으로 내려오면서 찾는 경우 생길 수도 있다.
클러스터의 크기가 크면 탐색과 삽입에 그만큼 시간이 소요되게 된다.
set(삽입), search(탐색), remove(삭제) 연산

공통으로 사용할 find_slot함수를 정의해서 set과, search 함수를 구현한다.

remove연산의 경우 set과 search연산과는 달리 추가적인 작업이 필요하다.
만약 클러스터의 중간값을 삭제하게 된다면, 클러스터는 끊기게 되는데, 이 경우 클러스터에 의해 값이 밀려서 뒤쪽에 저장된 데이터가 있는 경우라면, 연결이 끊기기 때문에 해당 key값을 찾을 수 없게 된다.
그렇기 때문에 조건에 따라 해당 데이터를 옮겨 주어야 하는 작업이 필요하다.

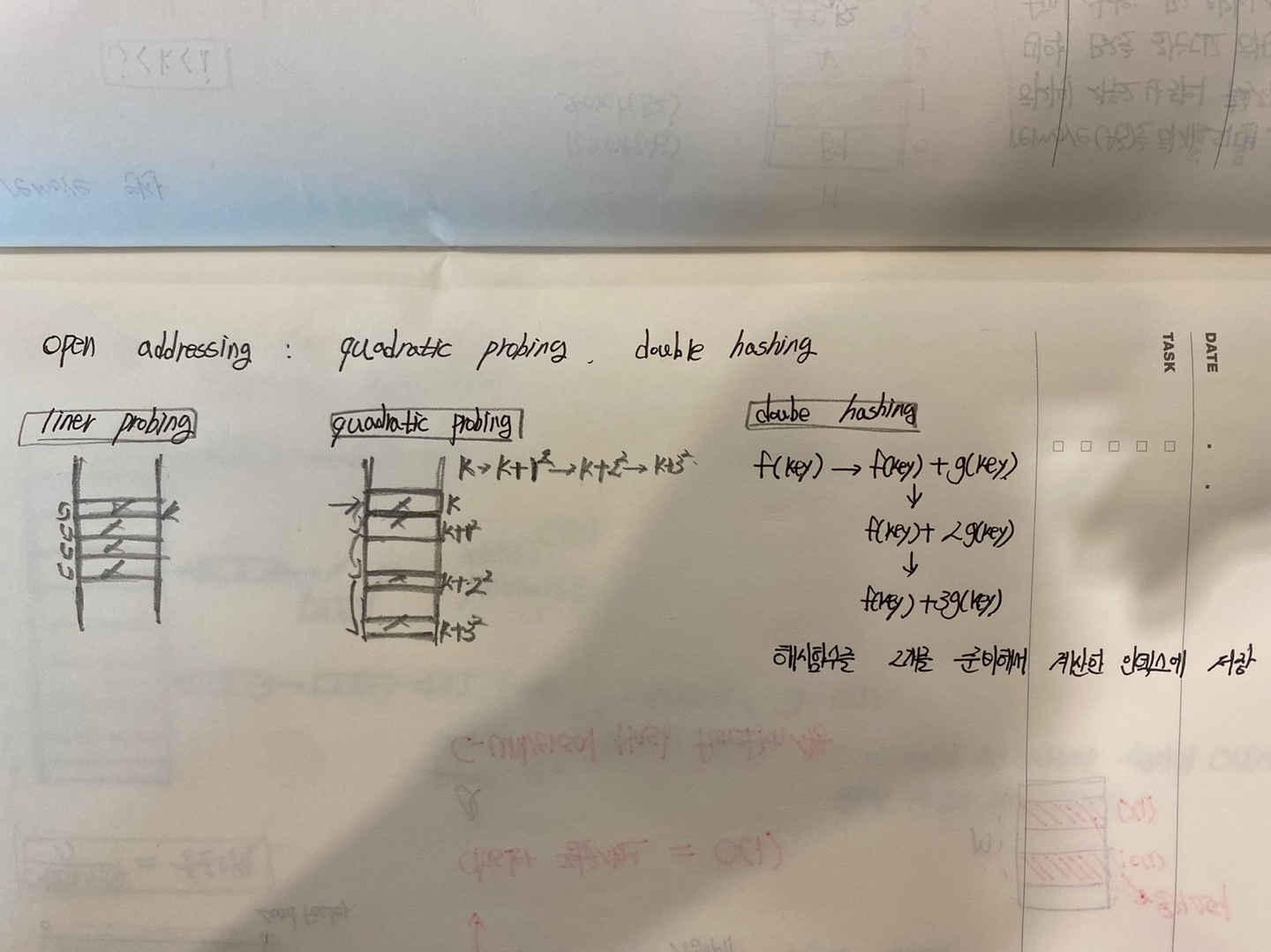
그 외의 Open Addressing

충돌회피 방법 - Chaining

Chaining기법은 만약 같은 해시함수 값을 가지게 되면 하나의 슬롯에 여러개의 데이터를 한방향 연결리스트를 이용해서 저장하는 방식을 의미한다.
참고
https://www.youtube.com/watch?v=Bzmepm6pYQI&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=17
https://www.youtube.com/watch?v=Bj4pd9rJp5c&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=18
https://www.youtube.com/watch?v=ghjWopXXUeA&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=19
https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/
