1번 표현법
앞의 트리에서 트리를 표현하는 방법에는 레벨을 이용한 표현법1
재귀표현법을 이용한 표현법2
노드 클래스를 이용한 표현법3이 있었다.
표현법1을 사용해서 트리를 표현할 경우 장점은 상수시간에 부모노드와 자식노드의 인덱스에 접근할 수 있다는 점이다.
왼쪽자식노드의 인덱스 = 2*현재노드인덱스 + 1
오른쪽자식노드의 인덱스 = 2*현재노드인덱스 + 2
부모노드의 인덱스 = (현재노드인덱스-1) // 2
위의 공식을 이용해서 상수시간에 접근이 가능하다.

Heap
Heap은 자료구조 Binary Tree의 종류 중 하나이다.
이진트리(Binary Tree)는 자식 노드의 수가 최대 2개를 가지는 트리 형태를 의미한다.
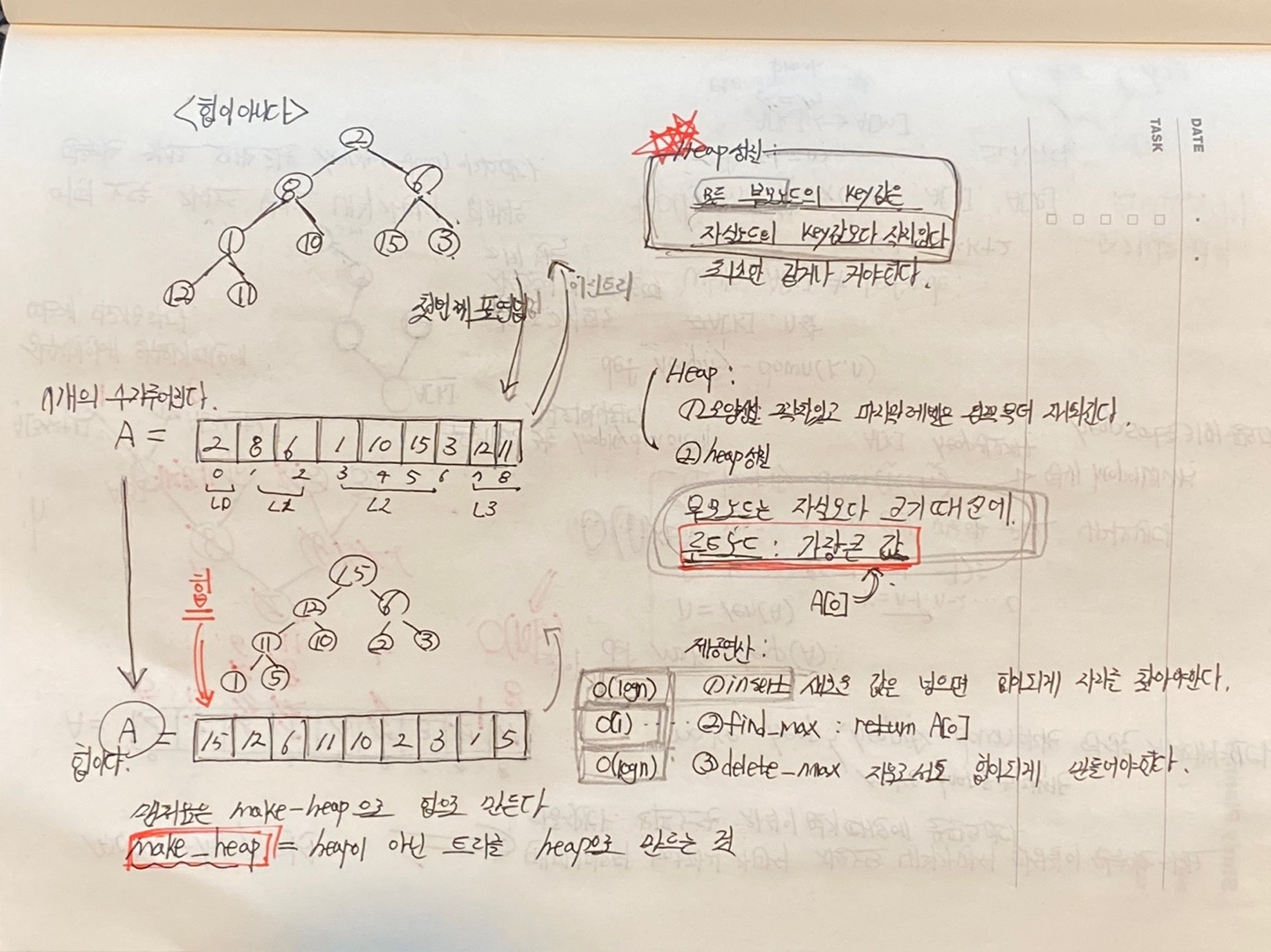
이진트리의 모습에 모양성질과 Heap성질을 만족하게 되면 Heap이 된다.
모양성질이란 자식노드 수가 최대 2개 이면서, 위에서 부터 아래로 꽉 채우면서 내려오며, 마지막 레벨에서는 왼쪽부터 차례대로 채워나가는 형태를 의미한다.
Heap 성질이란,
최대 힙의 경우는 부모노드는 자식 노드보다 최소한 크거나 같은 값을 가져야 한다. 이 성질은 루트노드부터 시작해서 아래로 내려가면 모든 노드가 만족해야되는 조건이다.
최소 힙의 경우는 최대 힙과 달리 부모노드가 자식노드보다 작거나 같아야 한다.
make-heap 연산
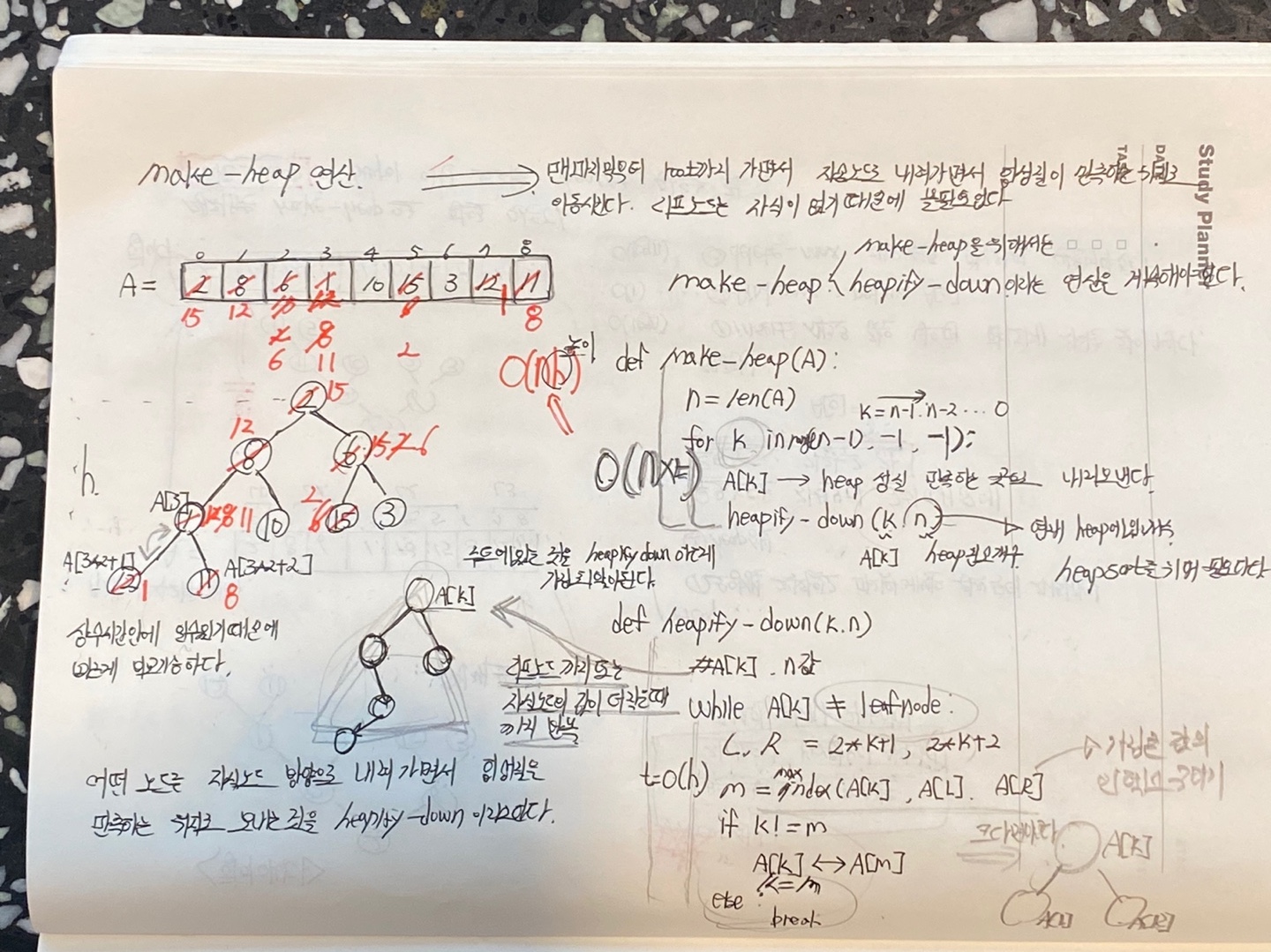
맨 마지막 노드부터 root로 가면서 해당노드의 자식노드로 내려가면서 힙 성질을 만족하는 위치로 이동시킨다.

n개의 노드로 이루어진 힙의 높이는 h이다.
위의 그림처럼 레벨별로 노드의 갯수는 2^h만큼 노드 수가 늘어나게 된다.
h-1에 해당하는 노드 갯수는 2^n-1이 된다.
맨마지막 h에 해당하는 노드갯수는 전체가 다 채워질수도 있고 1나만 채워질수도 있다.
전체를 합한값은 최소한 n보다 작거나 같게된다.
그러므로 공식을 이용해서 양변을 정리하면 h < log2N 이 된다.
insert 연산
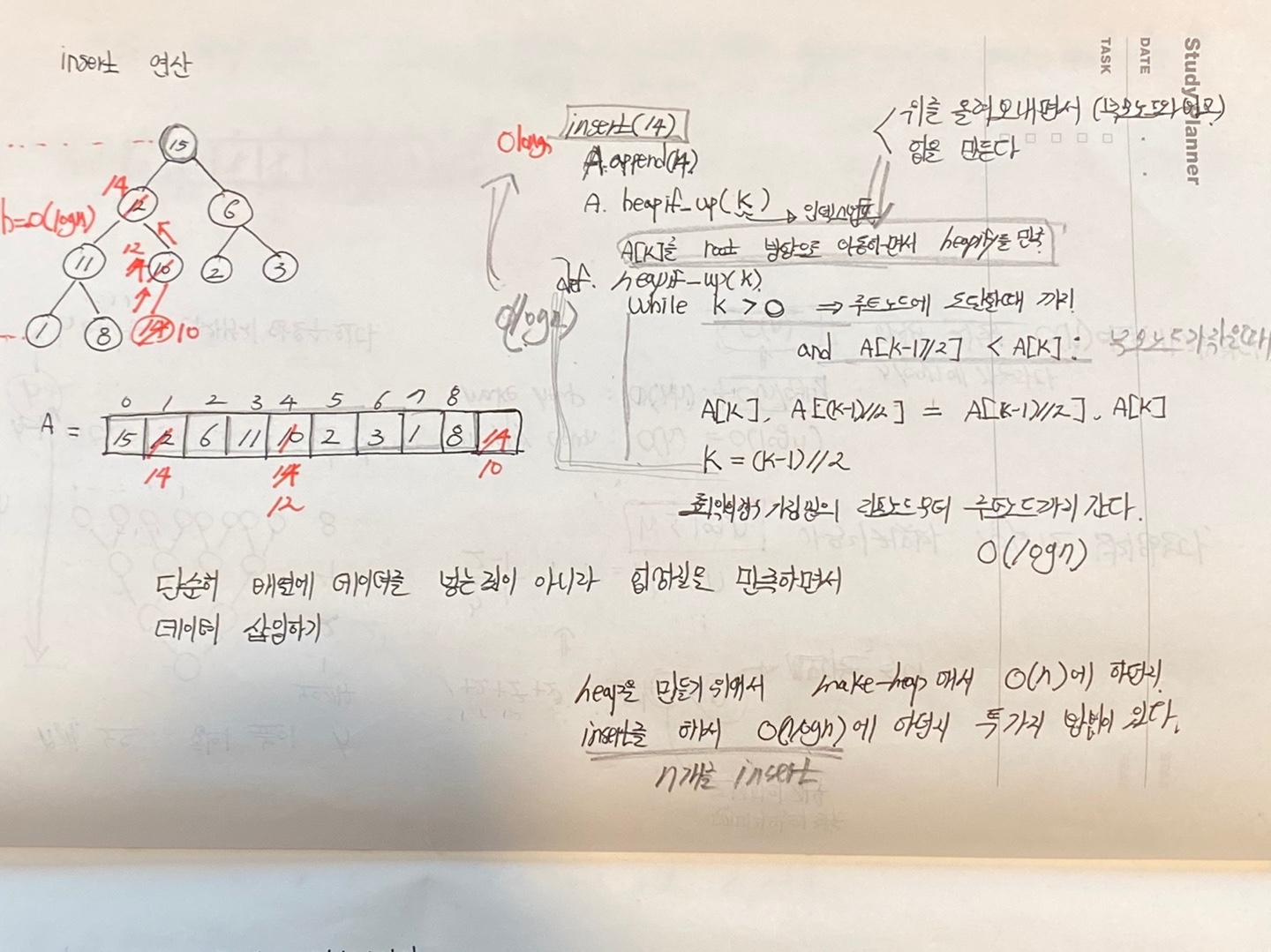
insert연산을 하게 되면 리스트의 맨마지막에 append를 하고서 heap성질이 만족하게 heapify-up()연산을 해준다.
heap을 만드는 방법은 기존의 리스트를 make_heap연산을 해서 만드는 방법도 있고, insert연산을 이용해서 바로바로 heap을 만드는 방법도 존재한다.
make_heap()연산의 경우 O(N) 하며 insert()연산의 경우는 O(NlongN)에 해당한다.
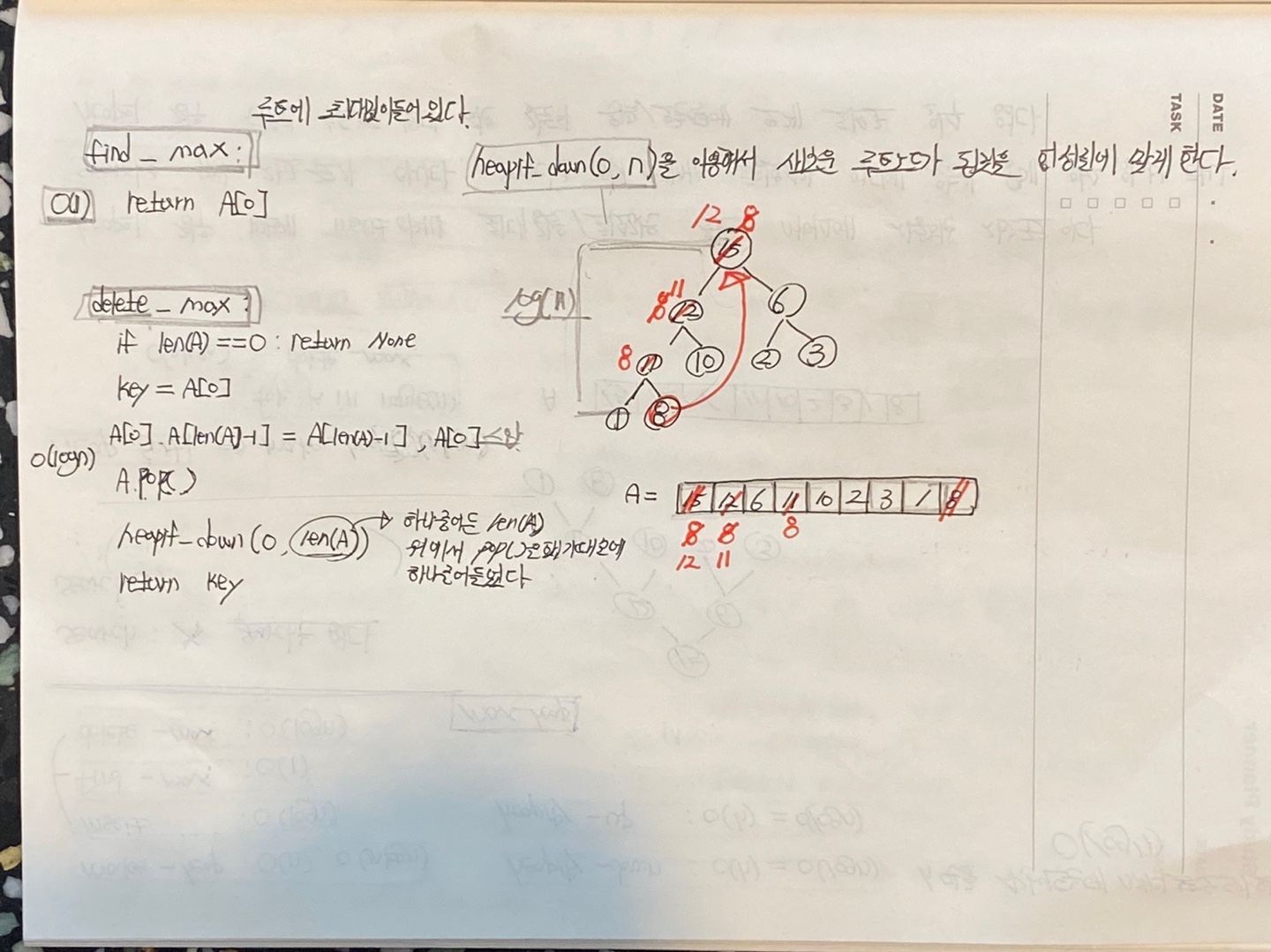
find_max 연산 & delete_max 연산
find_max의 경우 최대힙으로 구현했기 때문에 루트 노드에 해당하는 값을 반환하면 된다.
delete_max의 경우 root노드에 해당하는 값을 제거하고, 맨 끝에 있는 노드를 루트노드로 만들고 다시 heapify-down()연산을 해서 heap성질을 만족하게 하면 된다.
heap 결론
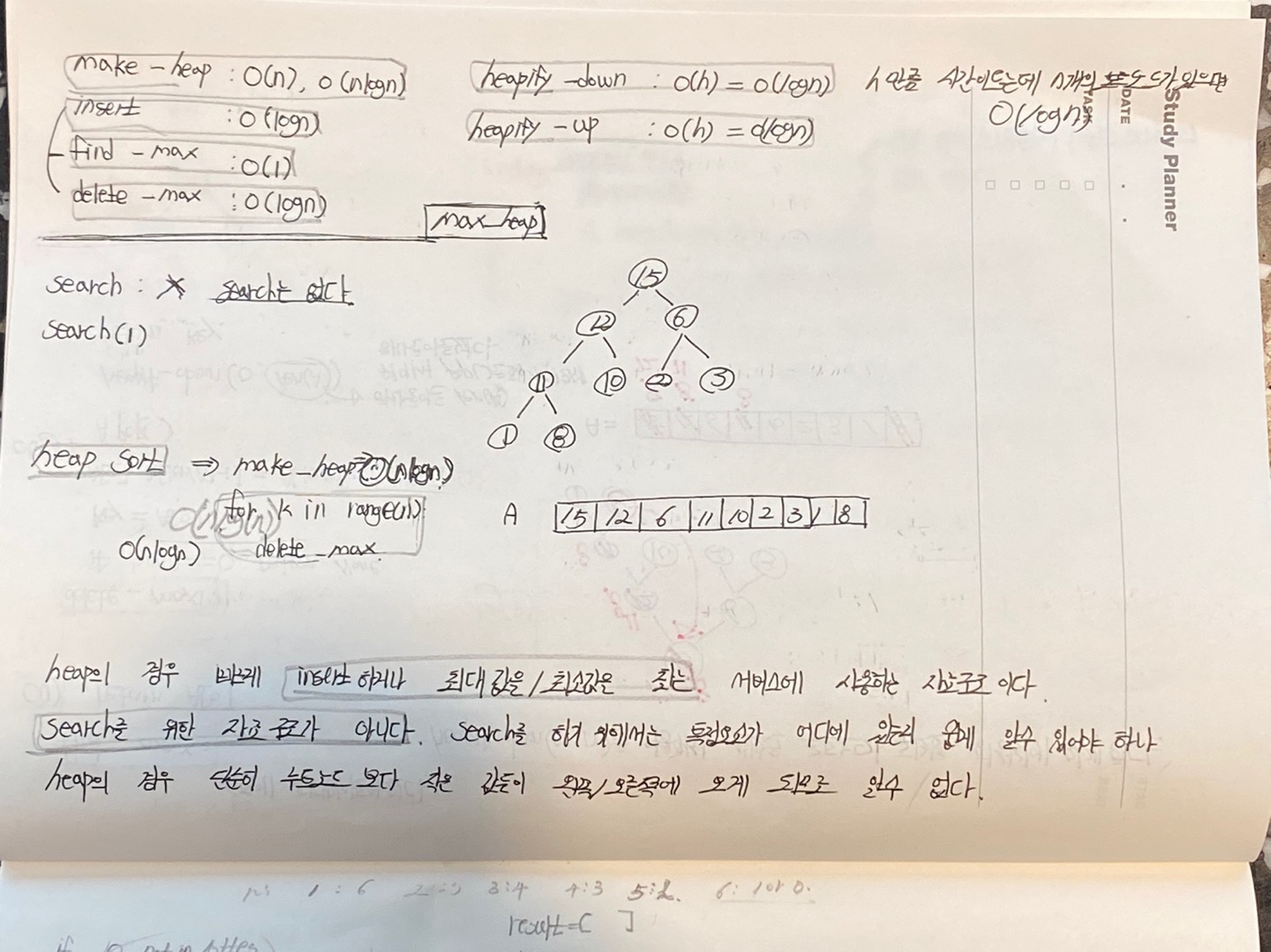
heap자료구조의 경우 search 연산은 없다.
heap은 빠른 삽입, 최대값 찾기를 사용하는 서비스에서 사용하는 자료구조이다.
search를 위한 자료구조에 해당하지 않는다.
데이터를 저장할 때 특정 요소가 어디에 있는지 판단하기 어렵기 때문에 search를 하고자하는 서비스에서 heap을 사용하는 것은 바람직하지 않다.
python heap 라이브러리
import heapq
a = [2,8,6,1,10,15,3,12,11]
heapq.heapify(a) # 최소힙으로 구성된다.
heapq.heappush(a, 4) # insert하면서 heap을 구성
heapq.heappop(a)
heapq.nlargest(3,a) # 리스트 내에서 크기가 큰 순으로 3개 구한다.
heapq.nsmallest(3,a) # 리스트 내에서 크기가 작은 순으로 3개를 구한다.
