[Data Structure] Queue

Queue

Queue는 Stack과 함께 대표적인 Sequential 자료구조이다.
Queue와 Stack의 공통점은 제한된 리스트에 비해 제한된 메서드를 제공한다는 점이다.

Stack이 LIFO정책을 따랐다면, Queue는 FIFO(First In First Out)정책을 따른다. 먼저 들어온 요소가 먼저 나가는 것이다.

위에 말했듯이 제한된 메서드만 제공하기 때문에, Queue는 중간에 데이터를 추가하거나 삭제하는 기능이 불가능하다.

Queue에 데이터를 삽입하는 메서드를 enqueue, 삭제하는 메서드를 dequeue라도 한다.

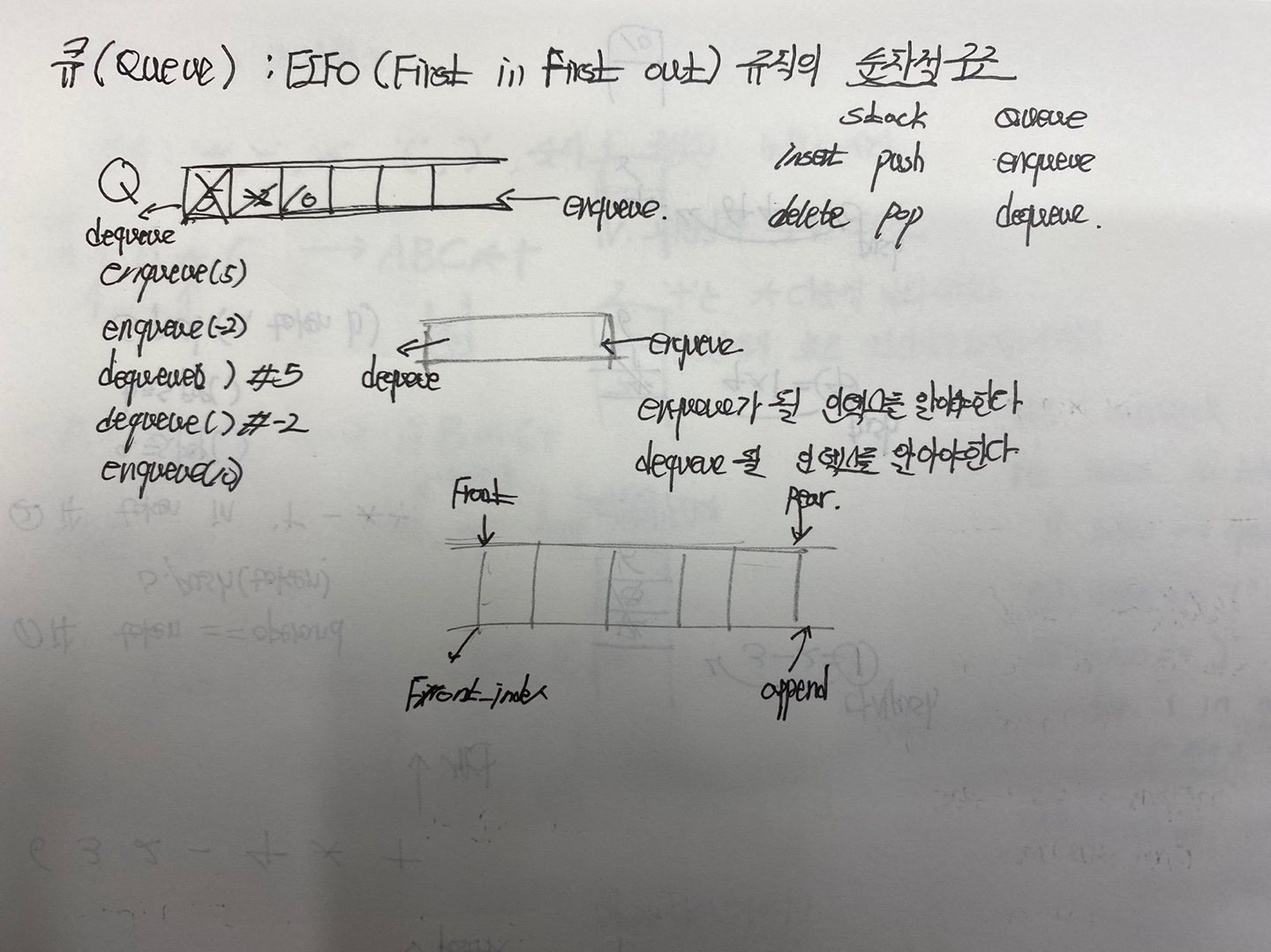
Queue에서 enqueue와 dequeue를 하기 위해서는 각각 어느 위치에 삽입되고, 어떤 위치의 요소가 삭제 될 것인지 알아야 한다.
enqueue의 경우는 단순한다. 맨 마지막에 추가하면 되기 때문에 크게 신경쓸 필요가 없다.

하지만 dequeue의 경우라면 이야기가 달라진다.
dequeue 맨앞의 요소를 삭제해주어야 한다. 예를들어 인덱싱을 사용한다면, [0] 번째 위치에 해당하는 요소를 찾아서 삭제하면 될 것이다. 하지만 다음에 다시 dequeue를 하기 위해서는 요소의 이동이 필요하다. 요소의 이동을 시키기 위해서는 현재 Queue안에 있는 모든 요소를 이동 시켜야 하기 때문에 O(n)의 시간복잡도가 발생하게 된다.

우리는 Queue에서 중간에 데이터를 추가하거나, 삭제가 불가능하다는 점을 알고 있고, 제한된 메서드로 enqueue와 dequeue만 가능하다는 것을 알고 있다.

그렇기 때문에 Front_index라는 인덱스 변수를 이용해서 삭제하는 효과만을 내며, 다음 삭제할 요소를 찾는 것도 가능하다. 또한 삭제 후에도 다른 요소의 추가적인 이동이 없기 때문에 O(n)의 시간 복잡도가 필요하지 않다.

queueu의 시간 복잡도는 O(1)상수가 된다.

class Queue:
    def __init__(self):
        self.items = []
        self.front_idx = 0

    def enqueue(self, val):
        self.items.append(val)

    def dequeue(self):
        if self.front_idx == len(self.items):
            return None
        else:
            x = self.items[self.front_idx]
            self.front_idx += 1
            return x

실제로 삭제하는 효과만들 내기 때문에 리스트에 요소들은 그대로 남아있고, front_idx만 이동하게 된다.
[⎜1,2,3,4,5] 이라는 queue가 있다고 가정하자!!

front_index와 front_index = 0 남아있는 요소들은 비교해서 이해해보자

1회 dequeue
self.front_idx = 1
return 1
1이 삭제되는 효과만 나고 다음 삭제할 요소를 2에 해당하는 1번째 인덱스로 이동시켰다.[1,⎜2,3,4,5]

2회 dequeue
self.front_idx = 2
return 2
2가 삭제되는 효과만 나고 다음 삭제할 요소를 3에 해당하는 2번째 인덱스로 이동시켰다.[1,2,⎜3,4,5]

3회 dequeue
self.front_idx = 3
return 3
3이 삭제되는 효과만 나고 다음 삭제할 요소를 4에 해당하는 3번째 인덱스로 이동시켰다.[1,2,3,⎜4,5]

4회 dequeue
self.front_idx = 4
return 4
4가 삭제되는 효과만 나고 다음 삭제할 요소를 5에 해당하는 4번째 인덱스로 이동시켰다.[1,2,3,4,⎜5]

5회 dequeue
self.front_idx = 5
return 5
5가 삭제되는 효과만 나고 다음 삭제할 요소를 6에 해당하는 5번째 인덱스로 이동시켰다.[1,2,3,4,5⎜]

실제로는 [1,2,3,4,5] 이 남아 있지만 모든 요소가 삭제된 것과 같다.
현재 front_idx = 5이면 queue의 길이는 5이다.
그러므로 여기서 다시 dequeue를 하게 되면, if을 돌게 되서 None이 반환된다.

	if self.front_idx == len(self.items):
            return None

Queue 활용 - 요세푸스 문제 (Josephus problem)

n과 k가 자연수이고, k < n이라고 가정한다. n명이 동그랗게 모여있을 때 임의의 한 명부터 순서를 세어 k번째 사람을 모임에서 제외한다. 남은 n-1명에서 다시 다음 사람부터 순서를 세서 k번째 사람을 모임에서 제외한다. 이것을 아무도 남지 않을 때까지 계속해서 반복한다. 이때 모임에서 제외되는 사람의 순서를 (n, k) 요세푸스 순열이라고 하며 마지막으로 제외되는 사람을 구하는 문제를 요세푸스 문제라고 한다. - 위키백과

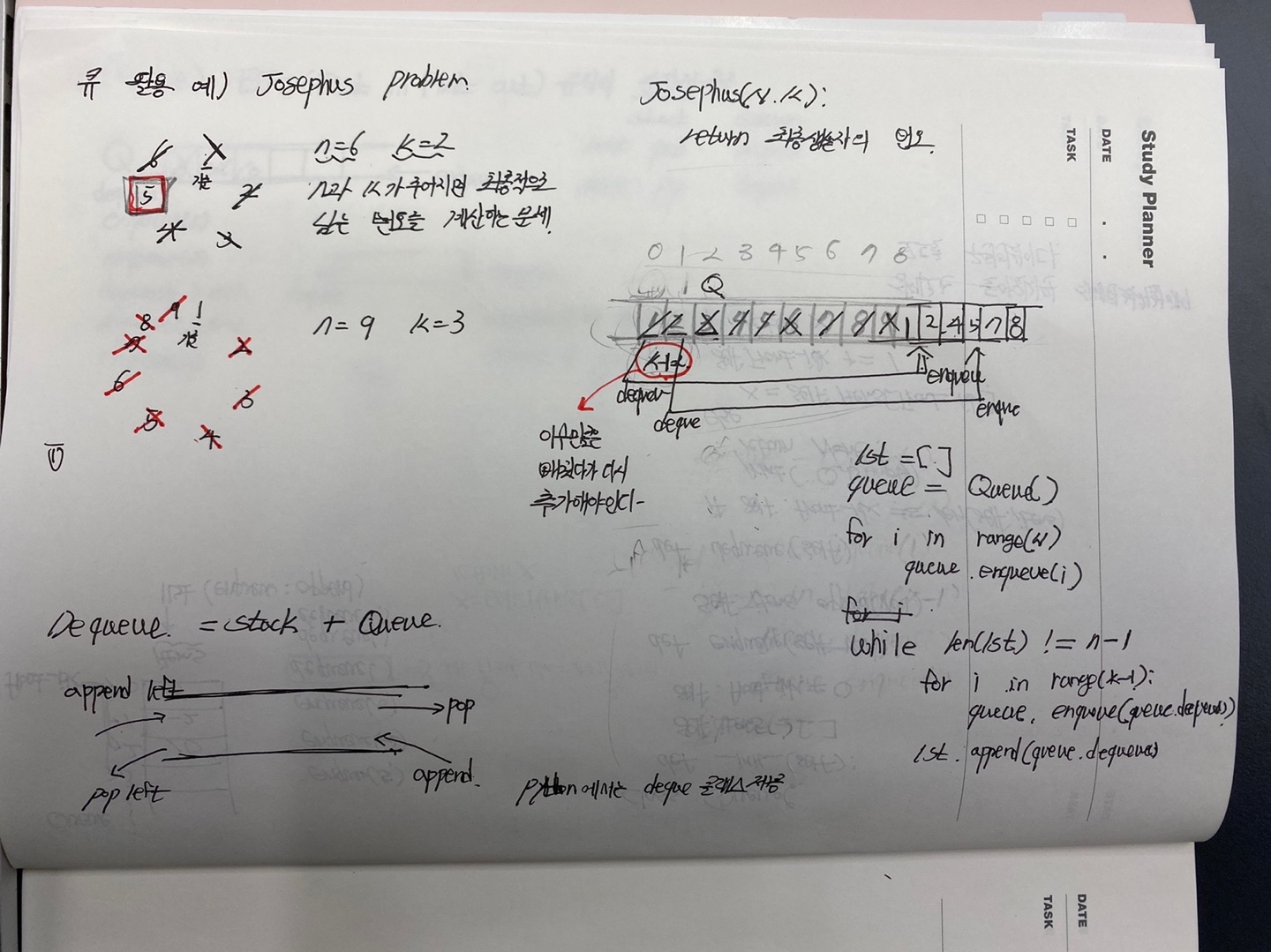
def josephus_problem(n,k):
    queue = Queue()
    lst   = []
    
    # queue에 1부터 n까지의 숫자를 담는 코드이다.
    for i in range(1, n+1):
        queue.enqueue(i)
	
    # dequeue된 요소들은 담은 lst의 길이와 한명이 남을 때 까지이므로 n-1과 같을 때 까지 계속해서 반복한다.
    while len(lst) != n-1:
        # k번째 사람이 나가게 되므로, 앞에는 k-1만큼의 사람이 있다.
        for i in range(k-1):
            queue.enqueue(queue.dequeue())
        # k번째 해당하는 사람을 lst에 담는다.
        lst.append(queue.dequeue())
    
    # 맨마지막에 해당하는 사람을 dequeue()한다
    return queue.dequeue()
    
n = 6
k = 2
result = josephus_problem(n, k)
print(result)

Dequeue 자료구조

Queue의 dequeue 메서드와 헷갈리 수 있으나, Dequeue라는 자료구조가 존재한다.

Dequeue는 Stack과 Queue를 합친 자료구조라고 생각하면된다.

Dequeue = Stack + Queue
자료의 삽입과 삭제가 앞과 뒤에서 모두 가능하다.
python의 경우 dequeue를 이용할 수 있는 클래스가 있다.

from collections import deque

a = deque([1,2,3])

a.append(4)
a.appendleft(5)

a.pop()
a.popleft()

deque에서 제공하는 다양한 메서드가 있다.
추가적인 메서드는 필요에 맞게 찾아서 사용하면 된다.

참고

https://www.youtube.com/watch?v=nqCNk_DmPio&t=1049s