
🤔 시간 복잡도(Time Complexity)?
시간 복잡도라는 개념를 알기 전에 먼저 알고리즘의 복잡도(Complexity) 계산이 필요한 이유를 아는 것이 중요하다. 어떤 문제를 해결하는데 있어서 나오는 알고리즘은 다양할 수 있다. 간단한 예로 주어진 정수 n의 절대값을 구하라는 문제가 있다.
- 정수 n을 제곱한 뒤, 그 값에 다시 루트를 씌운다.
- 정수 n이 음수인지 확인하고, 조건이 참이면 그 값에 -1을 곱한다.
이처럼 간단한 문제에서도 다양한 풀이 방법이 존재한다. 다양한 풀이 방법들 중 어느 알고리즘이 더 좋은지 분석하기 위해 복잡도를 정의하고 계산한다. 즉, 복잡도 계산은 가장 빠르게 실행되는 알고리즘을 찾는 방법이라고 볼 수 있다.
알고리즘 복잡도(Complexity) 표현 방식
알고리즘의 복잡도를 표현하는 방식에는 크게 두 가지가 있다. 바로 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)이다. 시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가리킨다. 쉽게 말해 알고리즘의 실행 속도(성능)을 계산하는 표현 방법이다. 공간 복잡도는 알고리즘에서 사용하는 메모리 크기를 말한다. 과거에는 메모리 가격이 비싸기 때문에 얼마나 적은 메모리를 차지하면서 알고리즘이 수행되는지가 중요했었다. 현재는 공간 복잡도보다 시간 복잡도가 더 중요하기 때문에 시간 복잡도에 대해 이해하고 계산할 수 있어야 한다. 알고리즘 시간 복잡도에 영향을 주는 주요 요소는 반복문이다. 반복되는 횟수가 많아질수록, 여러 반복문이 중첩될수록 시간 복잡도는 올라가게 된다.
알고리즘 성능 표기법
알고리즘 성능을 표기하는 방법은 크게 세 가지가 있다. 이 중 Big-O(빅 오) 표기법을 가장 많이 쓴다.
- Big-O(빅 오) 표기법: O()
알고리즘 최악의 실행 시간을 표기한다. 가장 많이 그리고 가장 일반적으로 사용하는 표기법이다. 아무리 최악의 상황이라도 최소 이정도의 성능은 보장한다는 의미이기 때문에 Big-O 표기법을 가장 많이 쓴다. - Big-(빅 오메가) 표기법: ()
오메가 표기법은 알고리즘 최상의 실행 시간을 표기한다. - Big-(빅 세타) 표기법: ()
세타 표기법은 알고리즘 평균 실행 시간을 표기한다.
Big-O(빅 오) 표기법
Big-O 표기법은 하나의 시간 복잡도 계산법이다. O()으로 표기한다. O()은 입력되는 에 따라 결정되는 시간 복잡도 함수이다. O(1), O(), O(), O(), O(), O(), O() 등으로 표기한다. 입력되는 n의 크기에 따라 시간 복잡도가 기하급수적으로 늘어날 수 있다.
시간 복잡도 크기 순서
O(1) < O() < O(n) < O() < O() < O() < O()
O() 이라면, 이 알고리즘은 로그 시간이 걸린다고 말할 수 있다. 컴퓨터가 이진수 시스템을 사용하기 때문에, 로그는 밑을 대부분 2로 사용한다. 와 는 오로지 상수 승수에 따라서만 달라지며 이것은 Big-O 표기법에서는 버림한다. 그러므로 O()은 로그의 밑과 상관없이 로그 시간 알고리즘에 대한 표준 표기법이 된다.
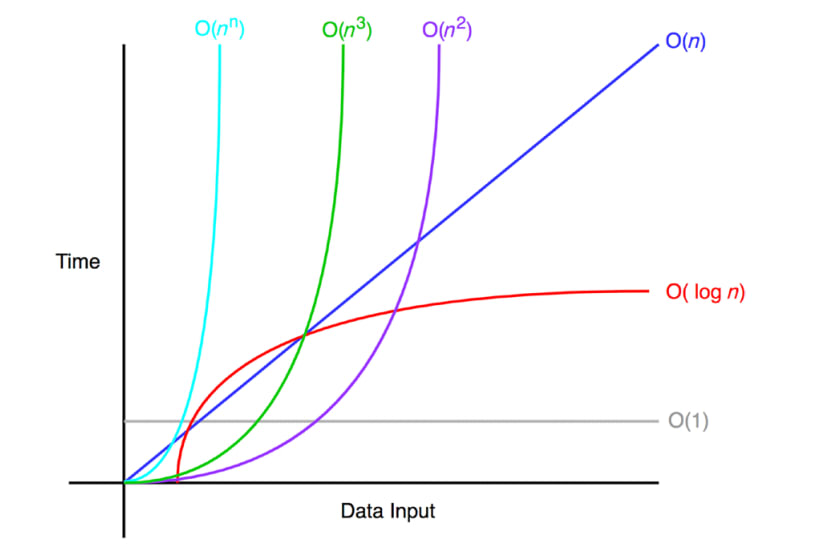
위의 그림은 입력 에 따른 O() 함수의 그래프이다. 축은 (Data input)이고, 축은 시간(Time)을 나타낸다. 위 그래프는 의 값에 따라 얼마만큼의 시간이 소요되는지 보여주고 있다. 같은 데이터가 들어와도 실행 시간이 다르다는 것을 알 수 있다.
Big-O 표기법의 시간 복잡도 표현 방법은 단순하게 입력되는 에 따라서 코드가 몇번 실행이 되는지 계산하면 된다. 만약 시간 복잡도 함수가 2 + 3이라면 가장 높은 차수는 2이 되고, 상수 2는 에 비해서 큰 영향이 없다. Big-O 표기법으로 표현하면 O()이 된다. 아래는 세 가지 예시 코드이다.
- O(1): 입력이 이든 1, 10, 100, 1,000, 10,000이든 어떤 수가 와도 상관없이 무조건 상수값 만큼 실행한다.
if (n > 0) {
console.log(n);
}- O(n): 입력 에 따라 , + 1, 3 + 1번 등 실행한다.
const array = [1, 2, 3, ... , 1,000,000]
for (let i = 0; i < 3; i++) {
for (const element of array) {
console.log(element);
}
}- O(): 입력 에 따라 , + 1,000, 3 + 3번 등 실행한다.
const variable = 1;
const array = [1, 2, 3, 4, 5, ... , 1,000];
const array2 = [1, 2, 3, 4, 5, ... , 1,000];
for (let i = 0; i < 3; i++) {
for (const value of array) {
for (const value2 of array2) {
console.log(value2);
}
}
}어느 알고리즘의 성능이 좋은가
1부터 n까지의 모든 수의 합을 구하는 알고리즘을 구현해보자.
// 알고리즘1
function sum(n) {
let total = 0;
for (let i = 1; i <= n; i++) {
total += i;
}
return total;
}
// 알고리즘2
function sum(n) {
const total = n * (n + 1) / 2;
return total;
}
sum(100) // 5050어느 알고리즘이 더 성능이 좋은지를 객관적으로 비교하기 위해 Big-O 표기법의 시간 복잡도 계산법을 사용하면 다음과 같다. 알고리즘1은 O(), 알고리즘2는 O(1)로 계산된다. 알고리즘2의 시간 복잡도 크기가 더 작기 때문에 성능면에서 더 좋다고 할 수 있다. 이처럼 동일한 문제를 해결할 수 있는 알고리즘은 다양하고 성능면에서도 차이가 발생할 수 있다.
📝 참고
wikipedia - 시간 복잡도
[이미지출처] DEV Community - Understanding Big-O Notation With JavaScript
